При естественном описании движения.
Пусть задана траектория движения точки М, а на ней указано начало О и положительное направление отсчета дуговой координаты s. Пусть также задано естественное уравнение движения точки (5.2).
 Рассмотрим радиус-вектор r точки М относительно какого-нибудь неподвижного центра С (рис.6). Зависимость радиус-вектора r=
Рассмотрим радиус-вектор r точки М относительно какого-нибудь неподвижного центра С (рис.6). Зависимость радиус-вектора r=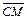 от времени можно рассматривать как сложную функцию r = r[s(t)]. Её производная по времени дает
от времени можно рассматривать как сложную функцию r = r[s(t)]. Её производная по времени дает  , где
, где 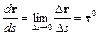 - единичный вектор касательной к траектории.
- единичный вектор касательной к траектории.
Итак, вектор скорости точки:
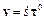 (5.13)
(5.13)
Чтобы получить ускорение, продифференцируем (5.13) по времени
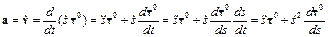 . (5.14)
. (5.14)
Последняя производная в правой части этого равенства может быть выражена (см. приложение 1) в виде
 , (5.15)
, (5.15)
где  - кривизна, r - радиус кривизны траектории; n0 - единичный вектор главной нормали, направленный к центру кривизны.
- кривизна, r - радиус кривизны траектории; n0 - единичный вектор главной нормали, направленный к центру кривизны.
Подставляя (5.15) в (5.14) находим

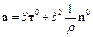 , (5.16)
, (5.16)
Это равенство означает, что вектор а ускорения точки имеет две составляющие: касательное ускорение
 , (5.17)
, (5.17)
направленное по касательной к траектории и нормальное ускорение
 , (5.18)
, (5.18)
направленное вдоль главной нормали к центру кривизны траектории (рис.7).
Пример 1. Векторное уравнение движения точки имеет вид:
r = (1 - 2 cost) i + sint j ( r – в м , t – в с ). (5.19)
Найти и построить траекторию точки. Определить скорость и ускорение точки в момент времени t1 = 3p /4 c.
Решение. Проецируя векторное равенство (5.19) на декартовы оси, получаем координатные уравнения движения точки:
x = 1 - 2 cost, y = sint , ( х , y – в cм) (5.20)
Чтобы получить уравнение кривой, являющейся траекторией точки, исключим из уравнений движения (5.20) время t . Для этого сначала преобразуем уравнения (5.20) к виду
 ,
, 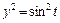 ,
,
а затем, складывая полученные уравнения почленно, находим

Как известно из аналитической геометрии, уравнение
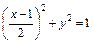
описывает эллипс с полуосями а = 2 см и b = 1 см и центром в точке С(1, 0). Этот эллипс (рис.8) и является траекторией точки.
Найдем положение точки в момент времени t1 = 3p /4 c. Для этого вычисляем значения координат точки в этот момент времени:
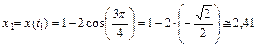 см ,
см ,
 см
см
Этим значениям координат соответствует точка М на рис.8.
Находим выражения проекций вектора v скорости точки на координатные оси, используя формулы (5.10):
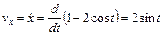 ,
, 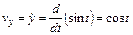
(здесь и далее точки над переменными означают дифференцирование по времени) .
Вычисляем значения проекций при  с :
с :
 см/c ,
см/c , 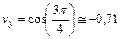 см/c .
см/c .
Находим модуль вектора скорости точки в момент времени  с :
с :
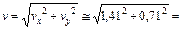 1,58 см/с.
1,58 см/с.
Выражения проекций вектора ускорения а точки на координатные оси находим, используя формулы (5.12):
 ,
,  .
.
Значения проекций, соответствующие моменту времени  с:
с:
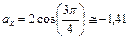 см/c2 ,
см/c2 ,  см/c2 .
см/c2 .
Модуль вектора ускорения при  с:
с:
 1,58 см/c2 .
1,58 см/c2 .

На рис.8 изображена траектория точки, её положение М в момент времени  с, а также вектор скорости v и ускорения a.
с, а также вектор скорости v и ускорения a.
Пример 2. Траектория движения точки – окружность радиусом R = 2 м. За начало отсчета дуговой координаты s выбрана точка А (рис.9), а за положительное направление отсчета – направление по ходу часовой стрелки. Естественное уравнение движения точки имеет вид:
s = 1 - 2t + t 2 ( s – в м , t – в с ). (5.21)
Найти положение этой точки, её скорость и ускорение в момент времени 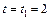 с.
с.
 Решение. Вычислим дуговую координату точки для момента времени
Решение. Вычислим дуговую координату точки для момента времени  с :
с :
s(2) = 1 - 2·2 + 22 = 1 м.
Чтобы установить положение точки М на окружности найдем величину центрального угла
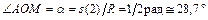 ,
,
и откладывая его от луча ОА в направлении хода часовой стрелки, построим положение точки М (рис.9).
Вычисляем скорость, касательное и нормальное ускорения точки согласно (3.13), (5.17), (5.18):
 ,
,
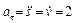 м/c²,
м/c²,  м/c².
м/c².
А также модуль ускорения точки
 м/c²,
м/c²,
На рис.9 показаны направления вектора ускорения а точки и его составляющих: касательного at и нормального an ускорений.