Затухающие колебания. - Лекция, раздел Философия, Часть 1. МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА При Выводе Уравнения Гармонических Колебаний Считалось, Что Колеблющаяся Точк...
При выводе уравнения гармонических колебаний считалось, что колеблющаяся точка находится под действием только квазиупругой силы. Во всякой реальной колебательной системе всегда имеются силы сопротивления (например, это может быть сила трения в точке подвеса, сопротивление среды, в которой совершаются колебания). Действие этих сил приводит к тому, что энергия колеблющейся системы (или точки) будет непрерывно убывать. Эта убыль энергии будет равна работе против сил трения и сопротивления. Т.к. полная энергия колебаний пропорциональна квадрату амплитуды 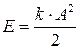 , то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих).
, то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих).
Итак, затухание колебаний в любой колебательной системе (механической, электрической и т.п.) обусловлено потерями энергии в этой системе. Потери энергии колебаний в механических колебательных системах происходят из-за трения (внешнего и внутреннего) и излучения упругих волн в окружающую среду; в электрических – из-за наличия активного сопротивления проводников и т.п.
Рассмотрим свободные (или собственные) колебания. Это значит, что система, будучи выведена из положения равновесия в результате внешнего воздействия, в дальнейшем предоставлена самой себе и находится под воздействием только квазиупругой силы F=-kx и силы сопротивления среды, значит она будет совершать затухающие колебания вдоль оси “x”.
Ограничимся рассмотрением малых колебаний, тогда и скорость (v) системы будет малой, а при небольших скоростях сила сопротивления пропорциональна скорости:
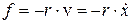 ,
,
где r – коэффициент сопротивления среды. Знак минус (“-”), т.к. 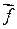 и
и  имеют противоположные направления.
имеют противоположные направления.
Под действием сил F и f тело приобретает ускорение “a”, и для колеблющегося тела уравнение II-закона Ньютона имеет вид:
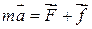 или
или 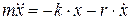 .
.
Обозначим 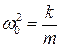 ;
; 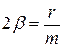 , тогда
, тогда
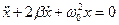
| (8.15)
| – дифференциальное уравнение затухающих колебаний
|
Здесь w0 – та частота, с которой совершались бы свободные колебания системы при отсутствии сопротивления среды (т.е. при r = 0). Эта частота называется собственной частотой колебаний системы. b – коэффициент затухания колебаний (зависит от свойств данной системы и среды).
Наличие сопротивления среды приводит к тому, что амплитуда колебаний со временем будет уменьшаться. Поэтому будем искать решение уравнения (8.15) в виде:
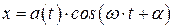
где a(t) – некоторая функция времени.
Продифференцируем это выражение по времени и найдем 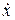 и
и 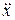 :
:

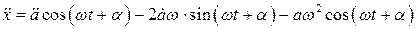
После подстановки этих выражений в уравнение (8.15) и несложных преобразований придем к следующему соотношению:
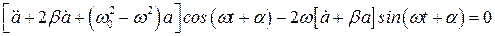 .
.
Для того чтобы уравнение удовлетворялось при любых значения “t”, необходимо равенство нулю коэффициентов при “sin” и ”cos”. Т.е. приходим к двум следующим уравнениям:
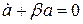
| (8.16)
|
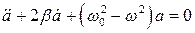
| (8.17)
|
Первое уравнение представим в виде:
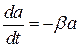 или
или 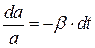 .
.
После интегрирования получим 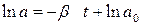 , где
, где 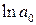 – постоянная интегрирования. После потенцирования найденного выражения получим
– постоянная интегрирования. После потенцирования найденного выражения получим 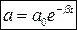 . Видно, что
. Видно, что 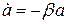 , а
, а 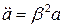 . Подставим эти значения в (8.17), получим
. Подставим эти значения в (8.17), получим
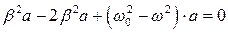 .
.
Отсюда 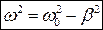 .
.
При w0 > b, величина w будет вещественной и тогда решение дифференциального уравнения 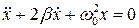 может быть представлено в виде
может быть представлено в виде
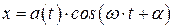 .
.
Таким образом, при не слишком большом затухании 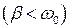 колебания описываются функцией
колебания описываются функцией
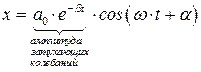 .
.
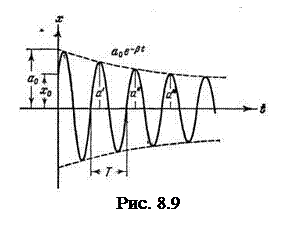
График этой функции показан на рисунке 8.9. Пунктирными линиями показаны пределы, в которых находится смещение колеблющейся точки. Движение такой системы можно рассматривать как гармоническое колебание с частотой w и амплитудой, изменяющееся по закону 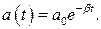 Верхняя из пунктирных кривых дает график функции a(t), причем величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы a:
Верхняя из пунктирных кривых дает график функции a(t), причем величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы a: 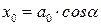 .
.
Скорость затухания колебаний определяется величиной 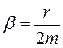 , которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению
, которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению 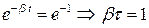 .
.
Следовательно, коэффициент затухания равен обратной величине того промежутка времени, за который амплитуда колебаний уменьшается в “e” раз.
С учетом того, что 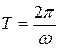 , а
, а 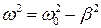 период затухающих колебаний можно определить как
период затухающих колебаний можно определить как
 .
.
При незначительном сопротивлении среды 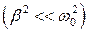 период колебаний практически равен
период колебаний практически равен 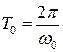 . С ростом коэффициента затухания период колебаний увеличивается.
. С ростом коэффициента затухания период колебаний увеличивается.
Для характеристики колебательной системы (а именно: убывания амплитуды колебаний в зависимости от числа колебаний) вводится величина, называемая логарифмическим декрементом затухания (l).
Отношение значений амплитуд, соответствующих моментам времени, отличающимся на период равно
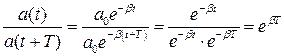
| – это отношение называется декрементом затухания, а его логарифм – логарифмическим декрементом затухания.
|
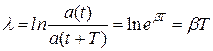 , т.е.
, т.е. 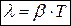 . Т.к.
. Т.к. 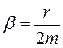 , то
, то 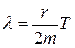 . Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды.
. Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды.
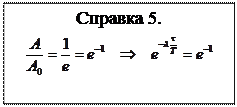 Выразим
Выразим 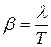 и запишем закон убывания амплитуды в виде
и запишем закон убывания амплитуды в виде 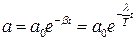 . За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит
. За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит 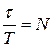 колебаний. Из условия
колебаний. Из условия 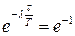 получаем
получаем 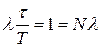 . Поэтому
. Поэтому 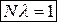 .
.
Следовательно, логарифмический декремент затухания равен обратной величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина).
величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина).
Для характеристики колебательной системы также часто употребляется величина 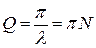 , называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз.
, называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз.
Как известно, энергия колеблющейся системы пропорциональна квадрату амплитуды. Поэтому энергия системы при затухающих колебаниях убывает со временем по закону
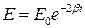 ,
,
где E0 – значение энергии при t = 0.
Продифференцировав это выражение по “t”, получим скорость возрастания энергии
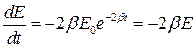 .
.
Изменив знак на обратный, найдем скорость убывания энергии: 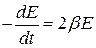 .
.
Если энергия мало изменяется за время равное периоду колебаний, то убыль энергии за период будет равна 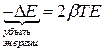 .
.
С учетом 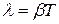 и
и 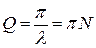 получим
получим 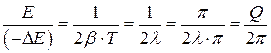 , т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.
, т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.
Из формулы для периода колебаний  следует, что с ростом коэффициента затухания период колебаний увеличивается, а при b = w0 период колебаний обращается в бесконечность, т. е., движение перестает быть периодическим.
следует, что с ростом коэффициента затухания период колебаний увеличивается, а при b = w0 период колебаний обращается в бесконечность, т. е., движение перестает быть периодическим.
И последнее, математический анализ показывает, что при условии 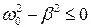 движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
Все темы данного раздела:
Несколько вводных замечаний о предмете физики.
Мир, окружающий нас материален: он состоит из вечно существующей и непрерывно движущейся материи.
Материей в широком смысле этого слова называется все, что реально существует в природе и м
Механика
Простейшим видом движения материи является механическое движение.
ОПРЕДЕЛЕНИЕ: механическое движение – изменение взаимного расположения тел или их частей относительно друг друга в простран
Кинематика движения материальной точки. Характеристики движения.
Положение материальной точки M в пространстве в данный момент времени может быть задано радиус-вектором (см. рис
Вектор скорости. Средняя и мгновенная скорость.
Движения различных тел различаются тем, что тела за одинаковые промежутки (равные) времени проходят различные по
Путь при неравномерном движении.
За малый промежуток времени Dt перемещение графически изображается в виде прямоугольника, высота которого равна
Ускорение при криволинейном движении (тангенциальное и нормальное ускорение).
Если траектория движения материальной точки представляет собой кривую линию, то такое движение мы будем называть криволинейным.
При таком движении
Угловая скорость.
ОПРЕДЕЛЕНИЕ: Вращательным движением будем называть такое движение, при котором все точки абсолютно твердого тела описывают окружности, центры которых лежат на одной прямой, называемой осью в
Угловое ускорение.
Вектор угловой скорости может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае
Связь между линейной и угловой скоростью.
Пусть за малый промежуток времени Dt тело повернулось на угол Dj (рис. 2.17). Точка, находящаяся на расстоянии R от оси, проходит при этом путь DS = R×Dj. По определению
Динамика
Раздел механики, исследующий законы и причины, вызывающие движение тел, т.е. изучает движение материальных тел под действием приложенных к ним сил.
В основе классической (ньютоновской) мех
II закон Ньютона.
ОПРЕДЕЛЕНИЕ: Ускорение всякого тела прямо пропорционально действующей на него силе и обратно пропорционально массе тела:
III закон Ньютона.
Всякое действие тел друг на друга носит характер взаимодействия: если тело M1 действует на тело M2 с некоторой силой f12, то и тело M2 в свою очер
Импульс. Закон сохранения импульса.
В механической системе, состоящей из нескольких тел, существуют как силы взаимодействия между телами системы, которые называются внутренними, так и силы взаимодействия этих тел с телами, не входящи
Работа и энергия.
Пусть тело, на которое действует сила , проходит, двигаясь по некоторой траектории путь S. При этом сила либо из
Мощность.
На практике имеет значение не только величина совершенной работы, но и время, в течение которого она совершается. Из всех механизмов наиболее выгодными являются те, которые за меньшее время выполня
Энергия.
Из опыта известно, что тела часто оказываются в состоянии совершать работу над другими телами.
ОПРЕДЕЛЕНИЕ: Физическая величина, характеризующая способность тела или системы тел совершать
Кинетическая энергия тела.
Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки).
Напишем уравнение движения частицы
Потенциальное поле сил. Силы консервативные и неконсервативные.
Если частица (тело) в каждой точке пространства подвержена воздействию других тел, то говорят, что эта частица (тело) находится в поле сил.
Пример: 1. Частица вблизи повер
Потенциальная энергия тела в поле сил тяжести (в поле тяготения Земли).
Поле тяготения Земли есть силовое поле, поэтому любое движение тела в силовом поле сопровождается совершением работы силами этого поля.
Для определения потенциальной энергии тела, находяще
Потенциальная энергия в гравитационном поле (в поле всемирного тяготения).
Установленный Ньютоном закон всемирного тяготения гласит:
ОПРЕДЕЛЕНИЕ: Гравитационная сила или сила тяготения – это сила, с которой две материальные точки притягивают друг др
Потенциальная энергия упруго деформированного тела.
Потенциальной энергией может обладать не только система взаимодействующих тел, но и отдельно взятое упруго деформированное тело (например, сжатая пружина, растянутый стержень и т.п.). В этом случае
Закон сохранения энергии.
Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частицы взаимодействуют друг с другом с силами
Поступательное движение твердого тела.
ОПРЕДЕЛЕНИЕ: Абсолютно твердым телом будем называть такое тело, деформациями которого в условиях рассматриваемой задачи можно пренебречь.
или
Абсолютно твердым телом
Вращательное движение твердого тела.
ОПРЕДЕЛЕНИЕ: Вращательным движением твердого тела будем называть такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и ой же прямой, называемой
Момент импульса тела.
Для описания вращательного движения потребуется ещё одна величина , называемая моментом импульса.
Снача
Основное уравнение динамики вращательного движения.
Рассмотрим систему материальных точек, каждая из которых может перемещаться, оставаясь в одной из плоскостей, проходящих через ось Z (рис. 4.15). Все плоскости могут вращаться вокруг оси Z с углово
Кинетическая энергия вращающегося твердого тела.
1. Рассмотрим вращение тела вокруг неподвижной оси Z. Разобьем все тело на множество элементарных масс m
Работа внешних сил при вращательном движении твердого тела.
Найдем работу, которую совершают силы при вращении тела вокруг неподвижной оси Z.
Пусть на массу действ
Линии и трубки тока.
Гидродинамика изучает движение жидкостей, однако ее законы примени- мы и к движению газов. При стационарном тече
Уравнение Бернулли.
Будем рассматривать идеальную несжимаемую жидкость, в которой внутреннее трение (вязкость) отсутствует. Выделим
Силы внутреннего трения.
Реальной жидкости присуща вязкость, которая проявляется в том, что любое движение жидкости и газа самопроизвольн
Ламинарное и турбулентное течения.
При достаточно малой скорости движения жидкости наблюдается слоистое или ламинарное течение, когда слои жидкости скользят относительно друг друга не перемешиваясь. При ламинарном т
Течение жидкости в круглой трубе.
При движении жидкости в круглой трубе ее скорость равна нулю у стенок трубы и максимальна на оси трубы. Полагая
Движение тел в жидкостях и газах.
При движении симметричных тел в жидкостях и газах возникает сила лобового сопротивления, направленная противоположно скорости движения тела. При ламинарном обтекании шара линии ток
Законы Кеплера.
К началу 17 столетия большинство ученых окончательно убедилось в справедливости гелиоцентрической системы мира. Однако ученым того времени не были ясны ни законы движения планет, ни причины, опреде
Опыт Кавендиша.
Первой успешной попыткой определения «g» были измерения, осуществленные Кавендишем (1798г.), который применил дл
Напряженность гравитационного поля. Потенциал гравитационного поля.
Гравитационное взаимодействие осуществляется через гравитационное поле. Это поле проявляет себя в том, помещенное в него другое тело оказывается под действием силы. Об «интенсивности» гравитационно
Принцип относительности.
В разд. 2.1. для механических систем был сформулирован следующий принцип относительности: во всех инерциальных системах отсчета все законы механики одинаковы. Никакими (меха
Постулаты специальной (частной) теории относительности. Преобразования Лоренца
Эйнштейн сформулировал два постулата, лежащие в основе специальной теории относительности:
1. Физические явления во всех инерциальных системах отсчета протекают одинаково. Никакими
Следствия из преобразований Лоренца.
Самым неожиданным следствием теории относительности является зависимость времени от системы отсчета.
Длительность событий в разных системах отсчета. Пусть в некоторой точк
Интервал между событиями.
В теории относительности вводят понятие события, которое определяется местом, где оно произошло, и временем, когда оно произошло. Событие можно изобразить точкой в воображаемом четырехмерном
Уравнение гармонического колебательного движения.
Пусть на некоторое тело массы “m” действует квазиупругая сила , под действием которой тело приобретает ускорени
Графическое изображение гармонических колебаний. Векторная диаграмма.
Сложение нескольких колебаний одинакового направления (или, что то же самое, сложение нескольких гармонических функций) значительно облегчается и становится наглядным, если изображать колебания гра
Скорость, ускорение и энергия колеблющегося тела.
Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного процесса.
Пусть имеем тело массы «m», которое совершает под действием квазиу
Гармонический осциллятор.
Систему, описываемую уравнением , где
Физический маятник.
ОПРЕДЕЛЕНИЕ: Физическим маятником будем называть твердое тело, способное совершать колебания вокруг непо
Вынужденные колебания. Резонанс.
Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колебаний на трение. Для того, чтобы энергия колебаний системы не убывала обычно вводят силу, пер
Предмет и методы молекулярной физики.
Молекулярная физика представляет собой раздел физики, изучающий строение и свойства вещества, исходя и так называемых молекулярно-кинетических представлений. Согласно этим представлениям любое тело
Термодинамическая система. Параметры состояния системы. Равновесное и неравновесное состояние.
ОПРЕДЕЛЕНИЕ: Термодинамической системой называется совокупность тел, обменивающихся энергией, как друг с другом, так и с окружающими телами.
Примером системы может служить жидкость
Идеальный газ. Параметры состояния идеального газа.
ОПРЕДЕЛЕНИЕ: Идеальным газом называется газ, при рассмотрении свойств которого соблюдаются следующие условия: а) соударения молекул такого газа происходят как соударения упругих шаров, размеры
Газовые законы.
Если разрешить уравнение состояния идеального газа
относительно какого-либо из параметров, н
Физический смысл универсальной газовой постоянной.
Универсальная газовая постоянная имеет размерность работы, отнесенной к 1 молю и температуре 1°К.
Основное уравнение кинетической теории газов
Если в предыдущем разделе применялся термодинамический метод исследования, то в этом разделе будет использован статистический метод исследования молекулярных процессов. На основании исследования со
Барометрическая формула. Распределение Больцмана
Давно известно, что давление газа над поверхностью Земли уменьшается с высотой. Атмосферное давление на некотор
Максвелловское распределение молекул по скоростям
В результате столкновений молекулы обмениваются скоростями, а в случае тройных и более сложных столкновений молекула может иметь временно очень большие и очень малые скорости. Хаотичное движение пр
Явления переноса. Длина свободного пробега молекул
В предыдущих разделах мы рассматривали свойства тел, находящихся в тепловом равновесии. Данный раздел посвящен процессам, с помощью которых происходит установление состояния равновесия. Такие проце
Явление диффузии
Диффузией называют процесс взаимного проникновения молекул соприкасающихся веществ, обусловленный тепловым движением. Этот процесс наблюдается в газах, жидкостях и твердых т
Явление теплопроводности и вязкости
Явление теплопроводности вещества определяет многие очень важные технические процессы и широко применяется в разнообразных расчетах. Эмпирическое уравнение теплопроводности было получено французски
Внутренняя энергия идеального газа
Важной величиной в термодинамике является внутренняя энергия тела. Любое тело кроме механической энергии может обладать запасом внутренней энергии, которая связана с механическим движением атомов и
Работа и теплота. Первое начало термодинамики
Внутренняя энергия газа (и другой термодинамической системы) может изменяться в основном за счет двух процессов: совершения над газом работы
Работа газовых изопроцессов
Пусть газ заключен в цилиндрический сосуд, закрытый плотно пригнанным и легко скользящим поршнем (рис.10.3). Пр
Молекулярно-кинетическая теория теплоемкостей
Теплоемкостью тела C называют физическую величину, численно равную количеству тепла, которое необходимо сообщить телу для нагревания его на один градус. Если сообщить телу к
Адиабатический процесс
Наряду с изопроцессами существует адиабатический процесс, широко распространенный в природе. Адиабатическим процессом называют процесс, протекающий без теплообмена с внеш
Круговые обратимые процессы. Цикл Карно
Механические процессы обладают замечательным свойством обратимости. Например, брошенный камень, описав некоторую траекторию, упал на землю. Если его бросить обратно с той же скоростью, то он опишет
Понятие об энтропии. Энтропия идеального газа
Для цикла Карно из формул (10.17) и (10.21) легко получить соотношение
Q1 /T1 - Q2 /T2 = 0. (10.22)
Величину Q/T называют
Второе начало термодинамики
Понятие энтропии помогло строго математически сформулировать закономерности, позволяющие определить направление тепловых процессов. Огромная совокупность опытных фактов показывает, что для
Статистическое толкование второго начала термодинамики
Состояние макроскопического тела (т.е. тела, образованного огромным числом молекул) может быть задано с помощью объема, давления и температуры. Данное макроскопическое состояние газа с определенным
Уравнение Ван-дер-Ваальса
Поведение реальных газов при их малых плотностях хорошо описывается уравнением Клапейрона:
Критическое состояние вещества
Важное значение уравнения Ван-дер-Ваальса заключается в том, что оно предсказывает особо
Эффект Джоуля-Томсона
В реальном газе между молекулами действуют силы притяжения и отталкивания. Силы притяжения обусловлены дипольным взаимодействием молекул. Некоторые молекулы могут представлять собой постоянные дипо
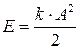 , то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих).
, то наличие сил трения и сопротивления приведет и к непрерывному убыванию амплитуды колебаний. Если убыль энергии не восполняется за счет работы внешних сил, то колебания будут затухать (и носят название затухающих).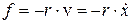 ,
,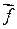 и
и  имеют противоположные направления.
имеют противоположные направления.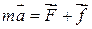 или
или 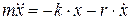 .
.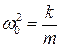 ;
; 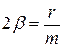 , тогда
, тогда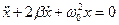
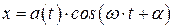
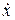 и
и 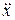 :
:
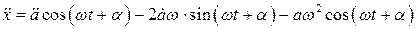
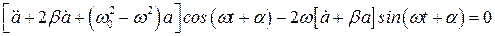 .
.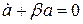
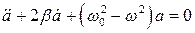
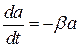 или
или 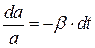 .
.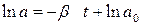 , где
, где 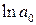 – постоянная интегрирования. После потенцирования найденного выражения получим
– постоянная интегрирования. После потенцирования найденного выражения получим 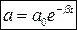 . Видно, что
. Видно, что 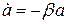 , а
, а 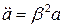 . Подставим эти значения в (8.17), получим
. Подставим эти значения в (8.17), получим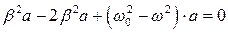 .
.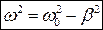 .
.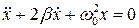 может быть представлено в виде
может быть представлено в виде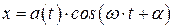 .
.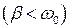 колебания описываются функцией
колебания описываются функцией
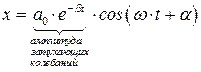 .
.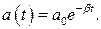 Верхняя из пунктирных кривых дает график функции a(t), причем величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы a:
Верхняя из пунктирных кривых дает график функции a(t), причем величина a0 представляет собой амплитуду в начальный момент времени. Начальное смещение x0 зависит, кроме a0, также от начальной фазы a: 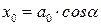 .
.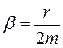 , которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению
, которую называют коэффициентом затухания. Найдем время t, за которое амплитуда колебаний уменьшается в “e” раз. По определению 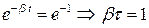 .
.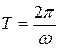 , а
, а 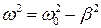 период затухающих колебаний можно определить как
период затухающих колебаний можно определить как .
.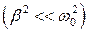 период колебаний практически равен
период колебаний практически равен 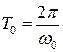 . С ростом коэффициента затухания период колебаний увеличивается.
. С ростом коэффициента затухания период колебаний увеличивается.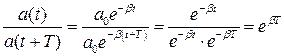
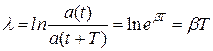 , т.е.
, т.е. 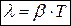 . Т.к.
. Т.к. 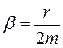 , то
, то 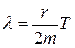 . Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды.
. Отсюда следует, что логарифмический декремент затухания l зависит от свойств данной системы и среды.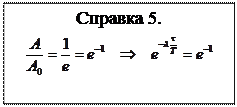 Выразим
Выразим 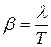 и запишем закон убывания амплитуды в виде
и запишем закон убывания амплитуды в виде 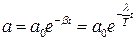 . За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит
. За время t, за которое амплитуда колебаний уменьшится в “e” раз система совершит 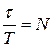 колебаний. Из условия
колебаний. Из условия 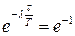 получаем
получаем 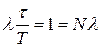 . Поэтому
. Поэтому 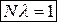 .
. величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина).
величине числа колебаний, совершаемых системой за то время, за которое амплитуда уменьшается в “e” раз (l – безразмерная величина).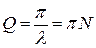 , называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз.
, называемая добротностью колебательной системы. Как видно из определения, добротность пропорциональна числу колебаний N, совершаемых системой за время t, за которое амплитуда колебаний убывает в “e” раз.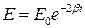 ,
,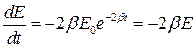 .
.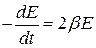 .
.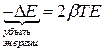 .
.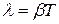 и
и 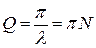 получим
получим 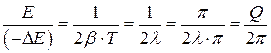 , т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний.
, т.е. при слабом затухании колебаний добротность с точностью до множителя 2p равна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний. следует, что с ростом коэффициента затухания период колебаний увеличивается, а при b = w0 период колебаний обращается в бесконечность, т. е., движение перестает быть периодическим.
следует, что с ростом коэффициента затухания период колебаний увеличивается, а при b = w0 период колебаний обращается в бесконечность, т. е., движение перестает быть периодическим.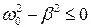 движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.
движение носит апериодический (непериодический) характер – выведенная из положения равновесия система возвращается в положение равновесия, не совершая колебаний.






Новости и инфо для студентов