Дифференциальное уравнение неразрывности потока

Рассмотрим жидкость, текущую без пустот и разрывов и при отсутствии источников массы. Выделим в объёме жидкости элементарный параллепипед объёмом dV = dxdydz, рёбра которого ориентированы параллельно осям координат (рис. 5).

Левая грань: площадь грани dS = dydz, составляющая скорости потока вдоль оси х в точках, лежащих на левой грани, - w_x , массовый расход жидкости: M=wSρ.

Тогда через эту грань в параллепипед войдёт вдоль оси x за единицу времени масса жидкости ρw_xdydz, а за промежуток времени dτ - масса жидкости М_х = ρw_xdydzdτ

 

 

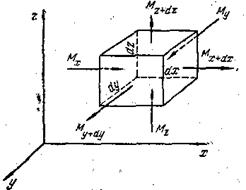
Рис. 5. К выводу дифференциального уравнения неразрывности потока

 

Правая грань: скорость (w_x + (w_x/x)dx);

плотность (ρ + (ρ/x)dx).

Тогда через правую грань за время dτ выйдет масса жидкости

М_{х + dx} = [ρw_x +((ρw_x )/ x)dx] dydzdτ.

Приращение массы жидкости в параллепипеде вдоль оси х

dM _x = M_x - М_{x+ dx} = - ((ρw_x )/ x)dxdydzdτ. Аналогично: dM _y = - ((ρw_y)/ y)dxdydzdτ, dM _z = - ((ρw_z )/ z)dxdydzdτ

Общее накопление массы жидкости (dM) в параллепипеде за время dτ равно сумме её приращений вдоль всех осей координат:

dM = - ((ρw_x )/ x + (ρw_y)/ y + (ρw_z )/ z) dxdydzdτ (3.8)

Вместе с тем изменение массы в полностью заполненном жидкостью объёме параллепипеда возможно только вследствие изменения плотности жидкости в этом объёме, то есть dM = (ρ/τ) dxdydzdτ (3.9).

Приравнивая оба выражения для dM (3.8) и (3.9), сокращая на (- dxdydz) и перенося ρ/τ в левую часть уравнения, получим:

ρ/τ + (ρw_x )/ x + (ρw_y)/ y + (ρw_z )/ z = 0 (3.10) –

это дифференциальные уравнения неразрывности потока для неустановившегося движения сжимаемой жидкости. В установившемся потоке плотность не изменяется во времени, т. е. ρ/τ = 0 и уравнение (3.10) принимает вид:

δ(ρw_x )/δx + δ(ρw_y)/δy + δ(ρw_z )/δz = 0 (3.11).

Для капельных жидкостей ρ = const, поэтому

ρ(w_x /x + w_y/y + w_z /z) = 0 (3.12),

ρ≠0, поэтому w_x /x + w_y/y + w_z /z = 0 (3.13) - дифференциальное уравнение неразрывности потока несжимаемой жидкости.

Чтобы перейти ко всему объёму жидкости, проинтегрируем уравнение (3.11), принимая, что площадь сечения трубопровода переменна. Получаем ρwS = const (3.14)- это уравнение неразрывности (сплошности) потока в интегральноц форме для установившегося движения. Для 3-х различных сечений трубопровода уравнение сплошности принимает вид: ρ₁w₁S₁ = ρ₂w₂S₂ = ρ₃w₃S₃ , М₁ = М₂ = М₃, т. е. при установившемся потоке, полностью заполняющем трубопровод, через каждое поперечное сечение проходит в единицу времени одна и та же масса жидкости. Поэтому уравнение (3.14) называют также уравнением постоянства расхода и оно является частным случаем закона сохранения массы и выражает материальный баланс потока. Для несжимаемых жидкостей ρ = const, поэтому уравнение (3.14) принимает вид: wS = const (3.15).