I. Средние величины.

Значение_средней в статистике. Среди обобщающих показателей, которыми широко пользуется статистика, большое значение имеют сред­ние величины. Применение средних величин объясняется тем, что ста­тистика изучает и характеризует совокупности по признакам, которые принимают разное количественное значение у отдельных единиц. Вели­чина признака у отдельных единиц складывается под воздействием ря­да причин как общих, так и индивидуальных. Отдельные наблюдения могут отражать влияние различных обстоятельств, в том числе и слу­чайных. В то же время существуют условия общие для всех единиц со­вокупности в целом.

Средняя величина и является тем обобщающим показателем, в ко­тором находят отражение эти общие условия.

Средней величиной в статистике называется обобщающая харак­теристика совокупности однотипных явлений по одному из количественно варьирующих признаков, которая показывает уровень признака отнесенный к единице совокупности. В средних величинах случайные колебания варьирующего признака погашаются, сглаживается влияние различных индивидуальных особенностей и в результате проявляется то, типичное, общее, что присуще всей совокупности в целом.

Средняя величина всегда является средней многих различных индивидуальных величин. Поэтому, чтобы средняя действительно харак­теризовала общий размер признака, присущий данной совокупности, не­обходимо основывать ее расчеты на большом числе наблюдений. Только при этом условии средние величины будут отражать общую тенденцию. Поскольку средняя обобщает многие индивидуальные величины одного и того же вида, то ее следует применять для характеристики качественно однородных совокупностей. Нарушение этого принципа приводит к искаженным данным, а средние, рассчитанные для неоднородной со­вокупности, дают ложную количественную оценку.

Необходимость соблюдать качественную однородность единиц, ха­рактеризуемых средней, требует предварительного их расчленения на однородные группы.

Поэтому расчету средних величин должен всегда предшествовать всесторонний общественно-экономический анализ, с помощью которого выделяются качественно однородные по типу группы, а затем для их характеристики применяют средние величины. Следовательно, метод средних должен быть тесно связан с методом группировок. Применение группировок позволяет избежать искажения действительности.

Средние величины широко используются для аналитических целей и в практике планирования. Различные плановые задания по отраслям народного хозяйства основываются на средних показателях таких как: средние нормы расхода сырья, материалов, топлива средняя производительность труда, средняя численность работников, средние на душу населения нормы потребления продуктов питания, средние тем­пы роста объема производства и т.д.

Широко используют средние величины в торговле: например» при расчете средних товарных запасов, цен, средней за­работной платы, среднего % выполнения плана и т.д. В товароведной практике средние величины применяются при разработке стандартов. Качественные нормативные показатели устанавливаются на основе средних величин, которые рассчитывают по данным большого количе­ства испытаний. Например, среднее содержание жира в сырье, сред­няя прочность ткани на разрыв, средняя продолжительность носки обуви и т.д.

Виды средних величин. Средние, которые применяют в статисти­ке, относятся к классу степенных средних. Общая формула степенной средней имеет вид:

, где

- степенная средняя;

x - величина признака у отдельных единиц;

n - число вариант;

m - показатель степени средней.

Значение показателя степени средней (m) определяет вид средней величины.

Если m=1, получается средняя арифметическая: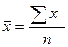

Если m =2, получается средняя квадратическая:

Если m =3, получается средняя кубическая. (На практике почти не используется.)

Если m = -1, то получается средняя гармоническая:

Если m =0, получается средняя геометрическая: , где П - знак перемножения (произведение отдельных значений х).

Из степенных средних в статистике применяются средняя арифметическая (наиболее часто), средняя гармоническая (реже), сред­няя геометрическая (при определении средних темпов динамики), средняя квадратическая (при исчислении показателей вариации).

Расчеты показывают, что при одних и тех же данных, разные ви­ды средних величин будут иметь разное значение. При этом, чем выше показатель степени, тем большое абсолютное значение средней вели­чины.

Например, X = 2 и X = 3. Следовательно, 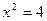; ; ; . Тогда:

; ;

;

В статистике правильную характеристику совокупности по варь­ирующему признаку дает в каждом случае только вполне конкретный вид средней величины. А установить какой именно вид средней вели­чины следует использовать для расчета, помогает теория.

Кроме степенных средних в статистике применяют особый вид средних величин: моду и медиану.

Средняя арифметическая, ее свойства и методика расчета. Наи­более распространенной формой средней, чаще всего применяемой в экономических расчетах, является средняя арифметическая. Средняя арифметическая используется в тех случаях, когда объем варьиру­ющего признака для всей совокупности образуется как сумма значе­ний признака у отдельных единиц. Различают среднюю арифметическую простую и взвешенную.

Среднюю арифметическую простую получают делением суммы отдельных значений признака на число этих значений.

Так, например, заработная плата (руб.) 5 рабочих составила: 180, 186, 188, 192, 194. Чтобы определить среднюю за­работную плату одного рабочего необходимо общую сумму заработной платы, выплаченную всем рабочим, разделить на их число:

Если заработную плату отдельных рабочих обозначить , а среднюю заработную плату через , то расчет средней арифметической простой в общем виде можно выразить формулой:

Таким образом, при определении средней арифметической прос­той суммируют все варианты и полученную сумму делят на их число. Следовательно, вычисление простой средней арифметической можно представить как расчет средней ряда распределения, в котором час­тоты всех_значений признака равны единице.

Однако на практике чаще всего встречаются ряды распределения, в которых значения признака повторяются.

Используя пример с заработной платой предположим, что бригада состояла не из 5, а из 20 человек, которые по размеру заработной платы распределились следующим образом:

Размер заработной платы (руб.) 180 186 188 192 194

Число рабочих 4 2 8 5 1

Очевидно, вычисление средней заработной платы по формуле простой средней арифметической невозможно, поскольку сумма вари­антов без учета их частот не будет равна сумме заработной платы, выплаченной всем рабочим. Чтобы получить общую сумму заработной платы необходимо умножить каждое значение признака на число рабочих, которым выплачена эта заработная плата и полученные произведения сложить. Такое умножение в статистике наз. взвешиванием, а число единиц, имеющих одинаковое значение признака, - весами или частотами. Если сумму полученных произведений разделить на число рабочих, то можно определить средний размер заработной платы од­ного рабочего.

Если, как и ранее, варианты признака обозначить "X", их частоты через “f “, то в общем виде расчет может быть представлен формулой:

Это и будет средняя арифметическая взвешенная дискретного ряда распределения. Расчет по этой формуле сделать во П случае легче, чем по формуле средней арифметической простой.

В интервальных рядах распределения расчет средней арифмети­ческой имеет свои особенности. Значение признака в интервальных рядах дано в виде интервала, т.е. указаны границы, в которых эти значения находятся. Поэтому, прежде чем делать расчет средней, ин­тервальный ряд преобразуют, в дискретный. Для этого по каждой группе интервалы заменяют на среднее значение, которое определяется как полусумма нижней и верхней границы интервала, после преобра­зования интервального ряда в дискретный среднее значение признака определяют по формуле средней, арифметической взвешенной.

Рассмотрим расчет средней арифметической взвешенной для ин­тервального ряда на примере:

Группы рабочих по размеру з/п (руб.)	Число рабочих	Среднее значение интервалов х	Произведение варианты на частоту
180 – 185		182,5
185 – 190		187,5
190 - 195		192,5
195 – 200		197,5

 

 

Если вариационный интервальный ряд распределения содержит интервалы с открытыми границами (например, в первой группе интер­вал может быть обозначен -до 185 руб. или в последней - свыше 195), то для расчета среднего значения интервала в этих группах условно определяют неизвестную границу, т.е. находят интервалы группиров­ки. Как правило, принимают для первой группы величину интервала равную интервалу последующей группы, а для последней - величину ин­тервала предыдущей группы.

Средняя арифметическая обладает определенными рядом матема­тических свойств, которые используются на практике и значительно упрощают ее расчет.