П. Показатели вариации

Изменение (колеблемость) величины изучаемого признака у раз­личных единиц совокупности в статистике называют вариацией, а по­казатели, характеризующие ее размеры, - показателями вариации.

Средние величины дают обобщающую характеристику совокупности, показывают типичный для данной совокупности уровень признака, но не позволяют судить о степени его колеблемости у отдельных единиц. Может оказаться, что в двух совокупностях признаки колеблются по-разному, а средние величины будут одинаковы.

Например, процент выполнения плана по двум цехам завода за пятидневку, характеризуется данными:

дни недели   % выполнения плана
цех № I цех № 2
I
102,5
97,5

В среднем за пятидневку 100 100

Как видно по приведенным данным, средний процент выполнения плана одинаков в обеих цехах – IOO%.

Однако цех № I работал более ритмично. Отклонение от планового задания по дням в этом цехе не превышало 2,5%,, тогда как в цехе № 2 оно изменилось OT -20% до +10%. Из этого примера видно, что од­ной средней величины для характеристики работы цеха оказывается не­достаточно. Поэтому средние величины необходимо дополнять показате­лями, характеризующими степень колеблемости признаков. Для измере­ния вариации в статистике используют несколько показателей.

При изучении количественно варьирующих признаков определяют:

1) размах вариации - R ,

2) среднее линейное отклонение – ;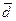

3) средний квадрат отклонений - (дисперсию) - ;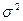

4) среднее квадратическое отклонение - ,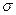

5) коэффициент вариации, -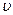

При изучении альтернативных признаков для характеристики степени их колеблемости рассчитывают:

1) дисперсию -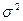

2) среднее квадратическое отклонение - .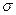

I. Размах вариации ( R ) - наиболее простая мера колеблемости, определяется как разность между максимальным и минимальным значе­ниями признака в совокупности (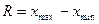). Выражается в тех же единицах измерения, что и варианты ряда. В нашем примере в первом случае R = 5% (102,5 - 97,5%) и во втором – R= 30% (110% - 80%). Но размах вариации имеет существенный недостаток. Размах вариации зависит от двух крайних значений признака, которые могут быть случайными, а не типичными для данной совокупности, по­этому он недостаточно точно характеризует колеблемость всех единиц совокупности в целом.

Размах вариации может иметь и самостоятельное значение. Напри­мер, в промышленности, где допуски точности изготовляемых изделий устанавливаются в определенных пределах, соответствующих иногда величине размаха вариации их признаков.

2. Среднее линейное отклонение (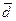) - показатель, характери­зующий среднюю величину отклонений вариант от среднего уровня. Для расчета этого показателя находят отклонение каждого значения приз­нака от средней. При этом всегда средняя величина вычитается из ва­рианты. Так как алгебраическая сумма отклонений и индивидуальных значений признака от средней равна нулю 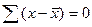(одно из свойств средней арифметической), то при исчислении среднего линей­ного отклонения принимаются во внимание только абсолютные значения отклонений, без учета знаков (+ или -).

Если варианты в ряду распределении не повторяются (частота каждой равна единице) или их веса равны между собой, то среднее линейное отклонений рассчитывается по формуле: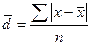

Для сгруппированных данных, когда варианты встречаются с разной частотой, среднее линейное отклонение определяется по формуле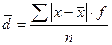

Среднее линейное отклонение для характеристики вариации приз­нака на практике используют редко. Недостаток этого показателя состоит в том, что линейное отклонение берется без учета знака. Кроме того, величину линейного отклонения различных вариационных рядов можно сопоставлять только в том случае, если эти ряды имеют одинаковые средние величины, и даются в одних единицах измерения .

Поэтому в статистике для характеристики колеблемости признака чаще всего пользуются дисперсией (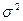) и средним квадратическим отклонением () .

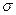3. Дисперсией (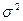), наз. средний квадрат отклонений индивидуальных значений признака от их, средней величины.

Чтобы определить дисперсию необходимо:

- найти отклонение каждой варианты от средней (),

- возвести эти отклонения в квадрат () ,

- умножить каждый квадрат отклонения на частоту, с которой встречается варианта ,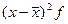

- полученные произведения суммировать.

Если сумму произведений квадратов отклонений на частоту разделить на сумму частот, то получим дисперсию признака ():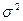

В тех случаях, когда частоты каждой варианты равны единице, дисперсия рассчитывается по формуле: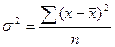

4. Среднее квадратическое отклонение (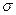) - равно корню квадратному из дисперсии :

Это формула среднего квадратического отклонения взвешенного. Если данные не сгруппированны, то расчет производят по формуле: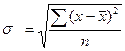

Среднее квадратическое отклонение является наиболее распрост­раненным и общепринятым показателем вариации. Выражается оно всегда в тех единицах измерения, в которых выражены варианта и средняя величины, и характеризует абсолютную меру вариации.

Среднее квадратическое отклонение широко используется в каче­стве показателя вариации не только в экономике, но и в технике, би­ологии и др. отраслях знаний.

5. Коэффициент вариации. По своему абсолютному значению среднее квадратическое отклонение зависит не только от степени колеблемости признака, но и от уровня вариант и средней. Поэтому сравнивать непосредственно квадратические отклонения в вариационных рядах с разны­ми уровнями средних нельзя.

Неприменим этот показатель и для сравнения степени колеблемости разноименных показателей, поскольку они будут иметь разную размер­ность.

Например, дисперсия (среднее кв. отклонение) себестоимость продукции исчисляется - в рублях, численности работающих - в кол. человек, рентабельности - в % и сопоставлять их по абсолютному значению нельзя. Кроме того, одна и та же по абсолютной величине дис­персия может иметь различное экономическое значение.

Чтобы иметь возможность такого сравнения, определяют коэффи­циент вариации.

Коэффициент вариации - процентное отношение среднего квадратического отклонения к средней арифметической.

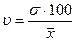
Коэффициент вариации дает относительную оценку вариации. Он позволяет сравнивать степень колеблемости признаков в одноименных совокупностях, но с разным уровнем средних, а также может исполь­зоваться для сравнительного анализа колеблемости признаков в совокуп­ностях, состоящих из разноименных или разномасштабных величин.

Так, например, среднее квадратическое отклонение норм выработ­ки по I бригаде = 10 деталей (при ), а во П бригаде 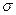= 9 деталей (при ). По абсолютной величине вари­ация норм выработки в I бригаде больше, а относительная мера вари­ации больше во П бригаде.

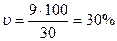
Коэффициент вариации в известной степени является критерием типичности средней. Если коэффициент вариации очень большой (выше 40%), то это значит, что средняя характеризует совокупность по приз­наку, который существенно изменяется у отдельных единиц. Типичность такой средней невелика и, следовательно, использовать ее для харак­теристики совокупности нецелесообразно.

Кроме коэффициента вариации могут использоваться и другие от­носительные показатели вариации: линейный коэффициент вариации и коэффициент осцилляции.

Процентное отношение среднего линейного отклонения к средней арифметической, наз. линейным коэффициентом вариации.

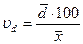
Отношение размаха вариации к сред­ней арифметической, выраженное в про­центах, наз. коэффициентом осцилляции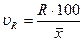

Для нашего примера с выполнением плана выпуска продукции по цехам завода коэффициент осцилляции составит:

1 бригада 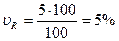II бригада

Оба эти показателя на практике используются крайне редко. На­иболее распространенным показателем колеблемости является все же коэффициент вариации.

Схему расчета показателей вариации можно рассмотреть на примере:

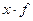
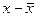
Средняя з/п рабочих Число рабочих Абсол. Откл.
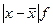
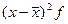
-18,3 18,3 79,2 334,89 1339,56
-8,3 8,3 68,89 1377,8
+1,7 1,7 2,89 86,7
+11,7 11,7 187,2 136,89 2190,24
      477,4   4994,3

 

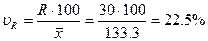
Дисперсия альтернативного признака. Среди варьирующих признаков встречаются такие, вариация кото­рых проявляется в том, что у одних единиц совокупности они имеются, а у других - нет. Признаки, которыми обладают одни единицы и не обладают другие, наз. альтернативными.

В раде случаев появляется необходимость измерить дисперсию альтернативных признаков. Наличие альтернативного признака прирав­нивается к единице, отсутствие - к нулю. Долю единиц, обладающих признаком, в общей совокупности принято обозначать " p ", а долю единиц не обладающих признаком - " q". Поскольку р + q= I, то q = 1 - p . Иногда значение q - заменяют на (I - р ) .

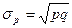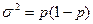Дисперсия альтернативного признака равна произведению доли единиц не обладающих признаком, на долю единиц, обладающих признаком, , а среднее квадратическое отклонение, или,а .

Чем меньше доля одного из признаков, тем меньше колеблемость, тем более однородна совокупность по изучаемому признаку. Наибольшая колеблемость бывает в тех случаях, когда абсолютное значение доли единиц, обладающих признаком и не обладающих признаком, одинаково - 0,5, тогда дисперсия альтернативного признака будет максимальной 0,25. Например:

Из опрошенных 100 чел. студентов 20 не получают стипендию

ОСНОВНЫЕ СВОЙСТВА ДИСПЕРСИИ И

УПРОЩЕНШЕ ПРИЕМЫ ЕЕ РАСЧЕТА

Дисперсия обладает рядом математических свойств, использование которых значительно упрощает и облегчает методику ее расчета.

I. Если все значения признака уменьшить или увеличить на какое-то постоянное число А, то средний квадрат отклонений от этого не изменится.

Следовательно, дисперсию можно исчислить не только по задан­ным вариантам, но и по их отклонениям от какого-то постоянного чис­ла А.

2. Если все значения признака разде­лить или умножить на какое-то постоянное число А, то дисперсия от этого уменьшится или увеличится в А2 раз.

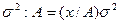
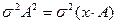
Следовательно, при расчете дисперсии можно все значения признака уменьшить в А раз, исчислить дисперсию, а затем умножить ее на это постоянное число в квадрате (А2 ) .

3. Сумма квадратов отклонений инди­видуальных значений признака (х) от их средней () меньше суммы квадратов отклонений индивидуальных значений признака от любого числа А, при усло­вии, что a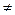x, т.е.

Это свойство дает возможность упрощать расчеты дисперсии путем замены громоздких отклонений индивидуальных значений признака от средней отклонениями любого произвольно взятого числа с последующей поправкой.

4. Дисперсия признака равна разности между средним квадратом значений признака и квадратом их средней, т.е.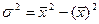

Расчет дисперсии и среднего квадратического отклонения является трудоемкой операцией. Так, используя данные примера, рассмотренного при определении средней величины методом условных моментов, можно определить дисперсию:

Средняя з/п рабочих Число рабочих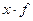
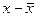
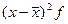
-18,3 334,89 1339,56
-8,3 68,89 1377,8
+1,7 2,89 86,7
+11,7 136,89 2190,24
      4994,3

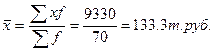
Этот расчет можно упростить, основываясь на приведенных мате­матических свойствах дисперсии.

Один из упрощенных способов определения дисперсии основан на применении свойства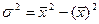

x f х2 х2f
   

Еще более значительно упрощаются расчеты дисперсии, а, следова­тельно, и среднего квадратического отклонения, если применить спо­соб условных моментов, в основе которого лежит равенство:

Чтобы определить дисперсию, основываясь на этом способе, нужно прежде всего исчислить момент второго порядка m2: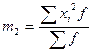

За величину "а" также принимаем 135 - (варианте, с наибольшей частотой), а за = величину интервала = 10.

x f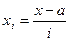
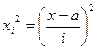
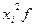
-2
-1
+1
     

Тогда

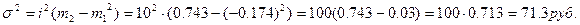
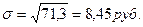
ПРАВИЛО СЛОЖЕНИЙ

На вариацию признака влияют различные причины. Их можно разделить на случайные и стематические.

Поэтому и вариация признаков м.б. случайной, под воздействием случайных причин, и систематической, которая связана с воздействием постоянных факторов.

При анализе возникает необходимость выделить вариацию случайную и систематическую, определить степень влияния каждой из них на общую дисперсию ().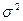

1. Общая дисперсия 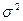- характеризует общую вариацию признака под влиянием всех факторов и определяется по формуле:

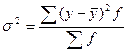
2. Межгрупповая дисперсия обусловлена фактором, положенным в основание группировки.

Для определения влияния на величину вариации постоянного Факто­ра пользуются аналитической группировкой, т.е. делят совокупность на группы по какому-либо признаку. Затем определяют степень влияния фактора, положенного в основу группировки, на общую дисперсию с по­мощью межгрупповой дисперсии .

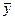Межгрупповая дисперсия характеризует колеблемость группо­вых средних () около общей средней () и определяется по формул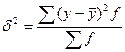е: , где

- среднее значение признака, в каждой группе,

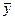- среднее значение признака во всей совокупности.

Таким образом, межгрупповая дисперсия равна средней арифметичес­кой из квадратов отклонений частных средних от обшей средней.

Она возникает под влиянием фактора, положенного в основу группировки и показывает силу влияния группировочного признака на об­разование обшей дисперсии.

3. Внутригрупповая дисперсия 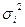. Для определения влияния на величину вариации случайных факторов определяют дисперсию в пределах каждой группы, т.е. внутригрупповую дисперсию, а затем среднюю из внутригрупповых дисперсий.

Внутригрупповую (частную) дисперсию определяют по ф-ле: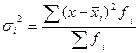

На величину внутригрупповых дисперсий группировочный признак влияния не оказывает. Чтобы получить представление об изменении обшей вариации под воздействием случайных факторов, определяют среднюю из внутригрупповых дисперсий по формуле: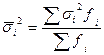

В математической статистике доказано, что общая дисперсия 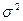равна сумме межгрупповой дисперсии и средней из внутригруппо­вых дисперсий .

Это правило наз. правилом сложения дисперсий.

Логика этого закона проста: общая дисперсия, возникающая под воздействием всех факторов, д.б. равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, обусловленной приз­наком, положенным в основание группировки.

Правило сложения дисперсий имеют теоретическое и практическое значение:

I) Зная любые два вида дисперсии, всегда можно определить правильность расчета третьего вида: или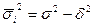

2) Зная общую дисперсию и дисперсию межгрупповую, можно судить о силе влияния группировочного признака на результативный.

Показатели общей и межгрупповой дисперсии используются в диспер­сионном и корреляционном анализе для оценки тесноты связи между приз­наками с помощью эмпирического корреляционного отношения.

Рассчитывают эмпирическое корреляционное отношение по формуле:

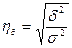
Значение 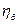— max (при ) и равно I. В этом случае влияние случайных признаков на результативный равно нулю.

Значение 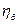- min (при ). В этом случае 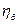=0, т.е. группировочный признак не оказывает влияние на результативный.

Промежуточные значения оцениваются по степени их близости к предельным. Чем ближе к I значение 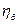, тем теснее связь.

Расчет показателей вариации и использование правила сложения дисперсий можно рассмотреть на примере:

Дан ряд распределения, по которому можно определить общую дис­персию и среднюю из групповых.

Распределение рабочих по выработке изделий

Группы рабочих Выработка изделий (шт.) y Число рабочих (f) yf
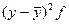
Не имеющих специальную подготовку -5,5 -3,5 -2,5 -1,5 30,25 12,25 6,25 2,25 242,0 134,75 37,5 33,75
Имеющих специальную подготовку +0,5 +1,5 +2,5 +4,5 0,25 2,25 6,25 20,25 4,25 40,50 87,5 222,75
        803,0

Общая средняя.

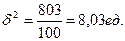
Определим внутригрупповую дисперсию в I группе. Прежде всего, на­ходим среднее значение признака в группе, используя ф-лу средней арифметической взвешенной

После определения , можно рассчитать дисперсию для I группы

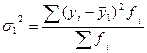
8-10,5=-2,5 6,25 6,25 X 8 = 50
10-10,5=-0,5 0,25 0.25 X 11= 2.75
11-10,5=+0,5 0,25 0.25 X 6 =1.50
12-10,5=+1,5 2,25 2.25 X 15 =33.75
    88.0

Затем определяем среднее значение признака во П группе

Рассчитаем дисперсию ( 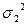) для второй группы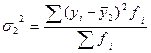

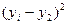
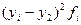
8-10,5=-2,5 6,25 6,25 X 8 = 50
10-10,5=-0,5 0,25 0.25 X 11= 2.75
11-10,5=+0,5 0,25 0.25 X 6 =1.50
12-10,5=+1,5 2,25 2.25 X 15 =33.75
    88.0

Чтобы определить среднюю из внутригрупповых дисперсий использу­ют ф-лу:

Теперь подсчитаем вариацию выработки, которая вызвана постоян­ным фактором, положенным в основу группировки (специальная подготов­ка) () - межгрупповую дисперсию. Используя ранее вычислительные 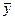= 13,5 ед., = 10,5 ед., 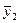= 15,5 ед., можно определить межгрупповую дисперсию.

По правилу сложения дисперсий