Энтропия вероятностной схемы. Основные свойства энтропии. Аксиомы Хинчина и Фадеева.
Простейший дискретный источник сообщений X в каждый фиксированный момент времени выдает некоторый символ  из конечного алфавита
из конечного алфавита
X = , с вероятностью P(
, с вероятностью P( )=
)=
Выборка символов производятся независимо друг от друга.
Воспользуемся аксиомами для определения количества информации:
1. Информация одиночного события  , происходящего с вероятностью pi имеет положительное значение:
, происходящего с вероятностью pi имеет положительное значение:
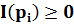
2. Совместная информация двух независимых событий 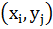 с совместной вероятностью
с совместной вероятностью 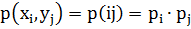 , равна сумме их информаций:
, равна сумме их информаций:

3. Информация является непрерывной функцией от вероятности события
Аксиомы 1 и 2 утверждают, что информация нескольких событий не может взаимно уничтожаться. Из аксиомы 3 следует, что небольшое изменение вероятности события приводит к небольшому изменению ее информации.
Кроме того, аксиома 2 вводит понятие совместной информации событий. Из аксиомы 3 следует, что информация определяется как логарифмическая функция от вероятности события.

 |
Вернемся к простейшему дискретному источнику, заданному вероятностной схемой Q→X={xi}, 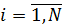 ,
, 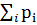 =1, 0≤
=1, 0≤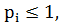
Тогда сообщение X источника является ансамблем полной группы {xi}, 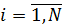 несовместных событий xi с вероятностями
несовместных событий xi с вероятностями  .
.
По аксиоме 2 средняя информация таких событий будет равна:
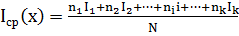 ,
,
где ni- частота появления i-го события;
k- количество разных событий;
Ii- информация i-го события;
Но 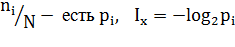 , тогда:
, тогда:
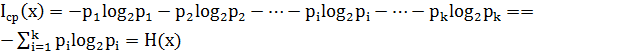 , где
, где 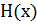 - Энтропия сообщения (ансамбля событий).
- Энтропия сообщения (ансамбля событий).
Основание логарифма в формуле определяет единицу измерения количества информации и энтропии.
Возможны другие обозначения двоичного логарифма: log2(x)=ld(x)=lb(x), где ld(x) – дуальный логарифм, lb(x) – бинарный логарифм. Такие обозначения можно встретить в зарубежной литературе. Единица измерения энтропии при использовании двоичного логарифма «бит» информации. Можно использовать и натуральный логарифм, при этом единица измерения информации «нат».
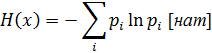
Измерение количества информации (энтропии) в битах хорошо согласуется с двоичной логикой, применением двоичной системы счисления, двоичным кодированием и двоичной (релейной) техникой.
Свойства энтропии:
1. Энтропия всегда неотрицательна, т.к. значение вероятностей всегда 

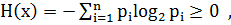
2. Энтропия равна нулю в том крайнем случае, когда вероятность одного из событий равна 1. Это случай, когда о сообщении (величине, опыте) все известно заранее и результат не приносит никакой новой информации.
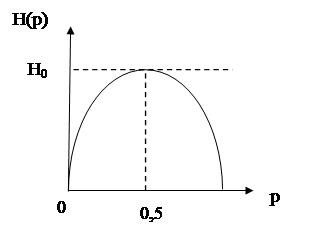
3. Энтропия сообщения максимальна, но при условии, когда события в нем равновероятны:
 ,
,

Это свойство определяет совпадение меры информации по Шеннону и по Хартли и служит для оценки потенциальной информационной емкости сообщения.
Вспомним меру Хартли 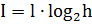 ,
,
где l – количество разрядов в сообщении;
h- алфавит сообщения;
Если рассмотреть один разряд l=1, то I1=log2h => I1=H0
В случае не равновероятных событий количество информации по Шеннону меньше информационной емкости системы.
Пример: Найти информационную емкость сообщения о двоичном событии (двоичной ячейки) и показать, как энтропия зависит от значений вероятности событий.
1. I= log2h; h=2; I=1 бит.
2. Если p1=p0=0,5, тогда
H0=
3. Если, например, p1=0,9, p0=0,1, тогда Р=-(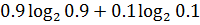 )=-[0,9(-0,152)+0,1(-3,32)]=0,46 => H1<H0 при p1≠p0
)=-[0,9(-0,152)+0,1(-3,32)]=0,46 => H1<H0 при p1≠p0
4. Если p1=1, p0=0, тогда
Р=-(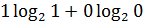 )=0. Событие достоверное.
)=0. Событие достоверное.
4.Энтропия аддитивна.
Задана объединенная вероятностная схема C=AB.
Пусть два сообщения A= и B=
и B=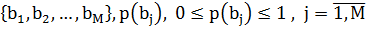 .
.
A и B независимы и составляют полную группу, т.е. 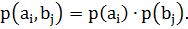
Тогда,
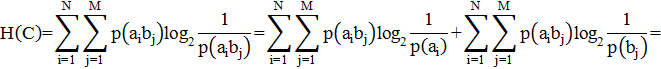
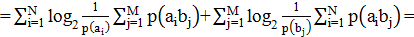

Энтропия непрерывных сообщений, при достаточно малом интервале квантования (∆x→0) может представляться выражением:
 , где p(x)- плотность распределения вероятности непрерывной величины x(t).
, где p(x)- плотность распределения вероятности непрерывной величины x(t).
Подходы Шеннона к определению количества информации сообщения длины l в условиях вероятностной схемы
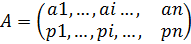 ,
, 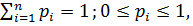 сопровождающейся следующими требованиями:
сопровождающейся следующими требованиями:
1. Пустое сообщение не содержит информации;
2. Количество информации, содержащееся в сообщении пропорционально его длине.
Сообщение T, записанное в алфавите A, с объемом H, имеет длину l: 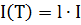 , где
, где 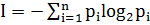 .
.
Энтропия вероятностной схемы или количество информации, приходящееся на один символ порожденного сообщения.
Хинчин и Фадеев через задание системы аксиом показали, что энтропия конечной вероятностной схемы однозначно определяется с точностью до постоянного множителя.
 , C
, C .
.