Приведем некоторые теоремы обобщающие исследования выше названных ученых.

Теорема. Если в каком-нибудь треугольнике сумма углов равна 2π, то это имеет место и во всяком другом треугольнике.

Ранее Лежандра эта теорема была доказана (в 1817 Г.) Н. И. Лобачевским, но опубликована им была лишь ее формулировка (в 1829 r).

Теорема Лежандра. Утверждение, что сумма внутренних углов хотя бы одного треугольника равна π, равносильно аксиоме параллельности Евклида.

Доказательство. Из аксиом I—IV и V групп (например, системы аксиом Гильберта) следует, что во всяком треугольнике сумма углов равна π. Доказатель­ство этого утверждения имеется в любом школьном учебнике геометрии. Докажем обратное: если к аксиомам I—IV групп добавить утверждение о том, что существует треугольник с суммой углов, равной π, то выполняется утверждение аксиомы о параллельных.

Прежде всего заметим, что согласно теореме 6 все треуголь­ники имеют сумму углов, равную π.

Пусть точка А не лежит на данной прямой а. Опустим из точки А перпендикуляр АР на прямую а и проведем через точку А прямую b, перпендикулярную к АР. Тогда прямые а и b не пересекаются. Надо доказать, что любая другая прямая с, проходящая через точку А, пересекает прямую а. Пусть Р - острый угол, который прямая с образует с перпендикуляром АР (рис. 8). Все дальнейшие построения будем проводить в полуплоскости α, ограниченной прямой АР, содержащей тот луч с' прямой с, который об­разует с лучом АР угол β. На прямой а в указанной полу­плоскости возьмем точку Р₁ так, что РР₁ = АР. Затем на луче РР₁ выберем точки Р₂, ..., Р_п-1, Р_п, ... так, чтобы

Р₁Р₂ = АР₁, Р₂Р₃ = АР₂, …, АР_n-1 = Р_п-1Р_п.

Рис. 8

Так как в каждом треугольнике сумма углов равна π, то в равнобедренных тре­угольниках АРР₁, AP₁P₂, ..., АР_п-1Р_п выполняются равенства

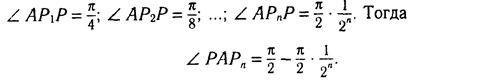
Так как β - острый угол, то существует такое веществен­ное число ε > 0, что 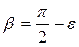. Выберем п так, чтобы выполня­лось неравенство . Тогда β < РАР_п. Поэтому луч с' пересекает сторону РР_п треугольника РАР_n, т.е. прямая с пересекает прямую а.

Теорема. Если сумма внутренних углов треугольника меньше π, то справедлив постулат Лобачевского.

Доказательство. Напомним постулат Лобачевского: существует такая прямая а и такая не лежащая на ней точка А, что через точку А проходит не меньше двух прямых, не пересекающих прямую а.

Через точку Р (рис. 9), не лежащую на прямой АА’ проведем прямую ВВ’ перпендикулярную к РQ, где РQ перпендикуляр к АА’. Покажем, что имеются прямые, отличные от ВВ', проходящие через точку Р и не пересекающие А А'.

Рис. 9

Соединим некоторую точку М, лежащую на АА', с Р и проведем луч PR так, чтобы угол MPR был равен углу PMQ. Из предположения о сумме углов треугольника вытекает, что угол MPB' > угла PMQ, т.е. луч PR пройдет внут­ри угла МРВ'; этот луч не пересекает АА', так как в противном случае получился бы треуголь­ник, у которого внешний угол QMP равен внутреннему MPR, с ним не смежному.

Таким образом, первая половина теоремы дока­зана, а из нее непосредственно вытекает обратное предложение.

При помощи доказанных теорем читатель может показать, что при формулировке постулатов Евклида и Лобачевского можно ограничиться более слабыми требованиями; например, постулат Евклида можно формулировать так: существуют прямая а и не лежа­щая на ней точка Р, обладающие тем свойством, что в плоскости, определяемой ими, через точку Р про­ходит не более одной прямой, не пересекающей а.

Теорема.Сумма внутренних углов треугольника на плоскости Лобачевского есть величина переменная (зависит от длины сторон).

Следствие 1. Сумма внутренних углов любого четырехугольника на плоскости Лобачевского меньше 4d.

Следствие 2. На плоскости Лобачевского не существует прямоугольников, а следовательно, и квадратов.

Теорема. На плоскости Лобачевского не существует подобных треугольников с коэффициентом подобия, отличным от единицы.

Следствие. На плоскости Лобачевского если три угла одного треугольника равны трем углам другого треугольника, то такие треугольники равны.