П.2 Предел функции.
Определение1. Число а называется пределом функции у=f(х), при х стремящемся к х0 (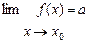 ), если для любой последовательности{xn} сходящейся к x0 последовательность{f(xn)=yn} сходится к а.
), если для любой последовательности{xn} сходящейся к x0 последовательность{f(xn)=yn} сходится к а.
Из определения 1 следует, что для предела функции справедливы все теоремы, справедливые для предела последовательности.
Определение2. Число а называется пределом функции у=f(x) при х стремящимся к х0 (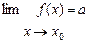 ),если "e>0 $ d>0 "х ½х-х0½<dÞ½f(x)-a½<e. Легко показать, что определение1 равносильно определению2. Мы будем пользоваться обоими этими определениями.
),если "e>0 $ d>0 "х ½х-х0½<dÞ½f(x)-a½<e. Легко показать, что определение1 равносильно определению2. Мы будем пользоваться обоими этими определениями.
Теорема1. (1-ый замечательный предел)
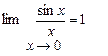
Доказательство.1)Пусть х>0, т.е. х-угол, измеренный в 

 радианах, лежащий в 1-ой четверти. Дан тригонометрический круг (окружность радиуса R=1). Рассмотрим треугольник ОАВ, сектор ОАВ и треугольник ОСВ.
радианах, лежащий в 1-ой четверти. Дан тригонометрический круг (окружность радиуса R=1). Рассмотрим треугольник ОАВ, сектор ОАВ и треугольник ОСВ.
SOAB< Sсектора< SOCB
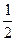 ОВ ·АН<
ОВ ·АН<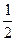 хR<
хR<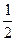 ОВ·СВ
ОВ·СВ
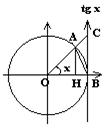 OB·AH<xR<OB·CB
OB·AH<xR<OB·CB
OB=R=1, AH=sinx, CB=tgx.
Таким образом 0<sinx<x<tgx. Поделим все части этого неравенства на sinx>0.
0<1<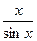 <
<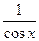 . Перевернём все дроби
. Перевернём все дроби
0<cosx<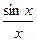 <1. (1)
<1. (1)
При х®0, cosx®1, 1®1.
По лемме о 2-х милиционерах 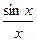 ®1при х®0.
®1при х®0.
2) Пусть -х<0, т.е. –х-угол в IV четверти. В неравенстве (1) везде вместо х подставим -х
cos(-x)=cosx, 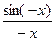 =
=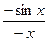 =
=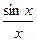
Ни одна величина в (1) не изменилась, значит неравенство справедливо при -хÎIV четверти. Теорема1 доказана.
Теорема2. (2-ой замечательный предел)
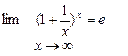 (или в равносильной формулировке
(или в равносильной формулировке 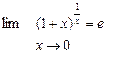 ).
).
Теорема3. (Бином Ньютона)
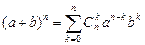 , где
, где 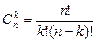
или в более подробной записи
(а+b)n=an+nan-1b+Cn2an-2b2+Cn3an-3b3+¼+Cnn-2a2bn-2+nan-1b+bn.