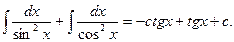Теорема4.(теорема Коши).
Пусть даны 2 функции f(x) и g(x) определённые и непрерывные на [a,b], дифференцируемые на (a,b), g`(x)¹0, " xÎ(a,b).Тогда $ сÎ(a,b), что
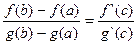 .
.
Доказательство.
Построим вспомогательную функцию Y(x)=f(x)-f(a)-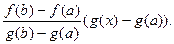
Покажем, что g(b)¹g(a). Если бы g(b)=g(a), то функция у=g(x) удовлетворяла бы теореме Ролля и тогда $ сÎ(a,b), что g`(c)=0, но по условию теоремы Коши g`(x)¹0 " xÎ(a,b).
Функция Y(x) удовлетворяет теореме Ролля ( легко показать самостоятельно). Поэтому $сÎ(a,b), что Y`(c)=0. Y`(x)=f`(x)-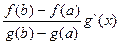
Y(c)=f`(c)-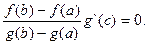 Отсюда
Отсюда 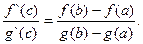
Раскрытие неопределённостей.
1) 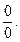 Рассмотрим 2 функции f(x) и g(x), f(x)=0
Рассмотрим 2 функции f(x) и g(x), f(x)=0 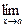 g(x)=0 (x), g(x) определены и дифференцируемы в некоторой окрестности точки а (за исключением может быть самой точки а). Если g`(x)¹0 в этой окрестности и существует конечный предел
g(x)=0 (x), g(x) определены и дифференцируемы в некоторой окрестности точки а (за исключением может быть самой точки а). Если g`(x)¹0 в этой окрестности и существует конечный предел 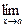
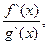 то
то 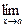
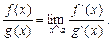
2) 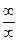 . Аналогично 1) пункту только
. Аналогично 1) пункту только 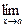 f(x)=¥ и
f(x)=¥ и 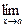 g(x)=¥
g(x)=¥
Такой способ вычисления пределов называется правилом Лопиталя.
Пример1. 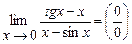
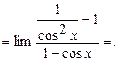
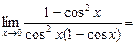
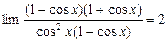
Пример2. 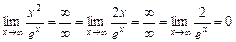
Решение примеров.
I. Вычисление пределов.
1. 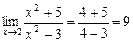
2. 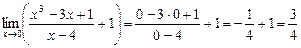 .
.
3. 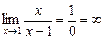
4. 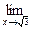
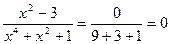
5. 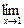
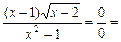
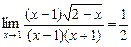
6. 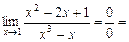
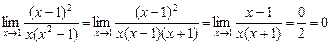
7. 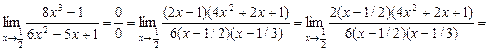
=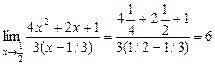
6x2-5x+1=0 x1,2=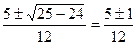 x1=1/2, x2=1/3
x1=1/2, x2=1/3
8. 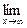
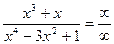 Разделим числитель и знаменатель дроби на х4 (наивысшая степень)
Разделим числитель и знаменатель дроби на х4 (наивысшая степень)
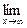
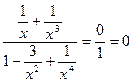 (
(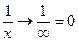
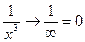 )
)
9 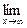
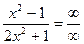
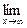
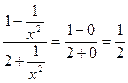
10. 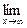
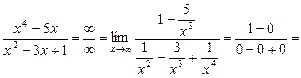 ¥
¥
11.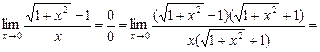
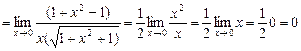
12. 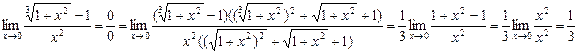
13. 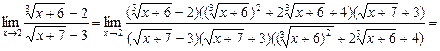
=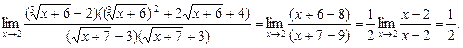
Применение 1-ого замечательного предела.
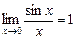 или
или 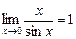
14. 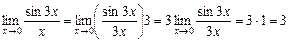
15. 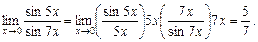
16.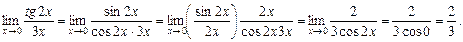
17. 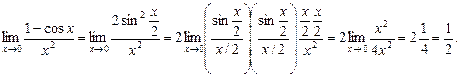
18. 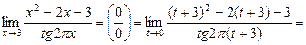
Пусть х-3=t при x®3 t®0 x=t+3
=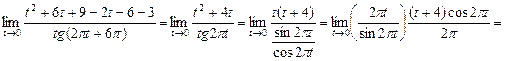
=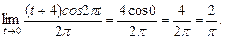
Применение 2-ого замечательного предела.
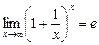 (1¥)
(1¥)
19. 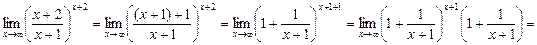
=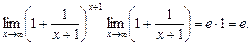
20. 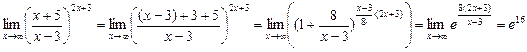
21. 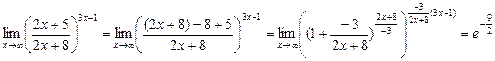
22. 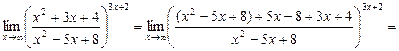
=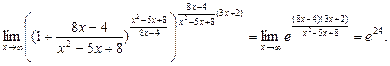
Вычисление производной.
1.y=cos2x, y`=(cos2x)`=-sin2x(2x)`=-2sin2x
2. y=etgx y`=(etgx)`=etgx(tgx)`=etgx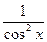
3. (arcsine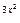 )`=
)`=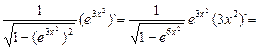
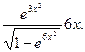
4. 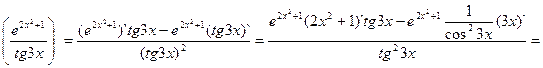
=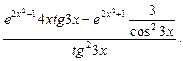
5. (log2sinx tglnx)`=(log2sinx)`tglnx+log2sinx(tglnx)`=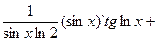
+log2sinx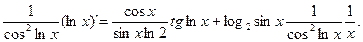
6. y=xshx прологарифмируем: lny=lnxshx; lny=shx lnx, продифференцируем выражение
(lny)`=(shx lnx)`; 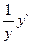 =(shx)`lnx+shx(lnx)`;
=(shx)`lnx+shx(lnx)`;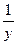 y`=chx lnx+shx
y`=chx lnx+shx 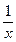 ;
;
y`=(chx lnx+shx 1/x)y; y`=(chx lnx+shx1/x)xshx;
7.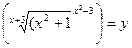
y=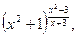 lny=ln
lny=ln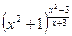
lny=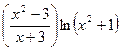 ; (lny)`=
; (lny)`=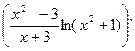 ;
; 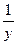 y`=
y`=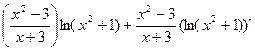 ;
;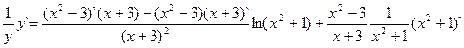
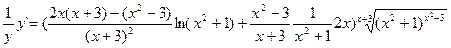 .
.
8. y=arcsin((chx)thx) (chx)`=shx, (thx)`=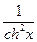 , (cthx)`=
, (cthx)`=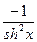
y`=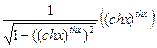
Рассмотрим вспомогательную функцию
u=(chx)thx lnu=ln(chx)thx (lnu)`=(thx ln chx)` 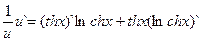
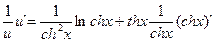
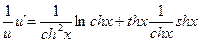
u`=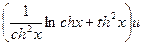 u`=
u`=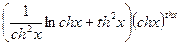
y`=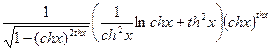 .
.
9. Провести касательную к гиперболе у=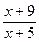 так чтобы она проходила через начало координат.
так чтобы она проходила через начало координат.
Т.к. гипербола не проходит через начало координат точку О (0,0) (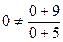 ), то точка О(0,0) - не точка касания. Пусть х0- абсцисса точки касания.
), то точка О(0,0) - не точка касания. Пусть х0- абсцисса точки касания.
Y=f(x0)+f `(x0)(x-x0)- уравнение касательной к линии у=f(x) в точке с абсциссой х0
y=f(x)=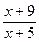 f(x0)=
f(x0)=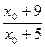
f`(x)=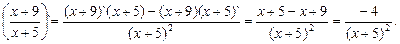
f`(x0)=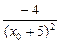
Тогда уравнение касательной к нашей гиперболе имеет вид
у=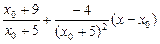 (1)
(1)
Воспользуемся тем, что касательная проходит через точку О(0,0),подставим в (1) вместо х и у координаты точки О.
0=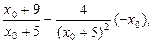 домножим на (х0+5)2 обе части равенства
домножим на (х0+5)2 обе части равенства
0=(x0+9)(x0+5)+4x0 x02+14x2+45+4x0=0
x02+18x0+45=0 x01=-3, x02=-15
Т.е. таких касательных 2.
Пусть х0=-3
y=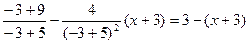 y=-x
y=-x
Пусть х0=-15
y=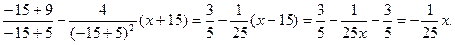
у=-1/25х.
Часть2. Интегрирование.
Неопределённый интеграл.
Определение1. Функция у=F(x) называется первообразной для функции у=f(x), если F`(x)=f(x).
Например для функции f(x)=cosx первообразной является функция F(x)=sinx, т.к. F`(x)=(sinx)`=cosx, для функции f(x)=x2- первообразная F(x)=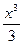 т.к. F`(x)=
т.к. F`(x)=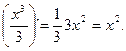
Теорема1.Если f(x) определена и дифференцируема на [a,b], f`(x)=0 " xÎ[a,b], то f(x)=C
(с-const).
Доказательство. Пусть х0- произвольная фиксированная точка отрезка [a,b], xÎ[a,b]-текущая точка. К отрезку [х0,х] (при х0<х) или [х,х0] (при х0>х) применима теорема Лагранжа, получаем
f(x)-f(x0)=f`(c)(x-x0), где сÎ[х0,х] (или[х,х0]) но f`(x)=0, т.к.cÎ[a,b], значит f(x)=f(x0).
Т.е. значение функции в любой точке х равно значению функции в фиксированной точке т.е. f(x)- постоянная.
Теорема2.Если F(x)- первообразная для f(x), то F(x)+c- первообразная для f(x) и других первообразных нет.(здесь с- произвольное число).
Доказательство. а) Докажем, что F(x)+c- первообразная для f(x).
(F(x)+c)`=F`(x)+c`=f(x)+0=f(x),т.е.F(x) первообразная для f(x).
б) Пусть F1(x) и F2(x)- две первообразные для f(x).
Тогда (F1(x)-F2(x))`=F1`(x)-F2`(x)=f(x)-f(x)=0.
Следовательно по теореме1
F1(x)-F2(x)=const F1(x)-F2(x)=c, F1(x)=F2(x)+c.
Таким образом, если F(x)- первообразная для f(x), то F(x)+c- множество всех первообразных для f(x).
Определение2. Неопределённым интегралом 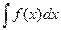 от функции f(x) называется множество всех первообразных для f(x) т.е.
от функции f(x) называется множество всех первообразных для f(x) т.е. 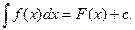
Свойства неопределённого интеграла.
1°. 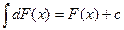
2°. d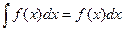 или
или 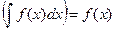
3°. 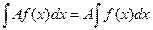
4°. 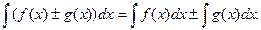
Если у=f(x), то dy=f `(x)dx.
Доказательство этих свойств изучить самостоятельно.
Таблица интегралов. 
0. 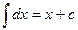
1. 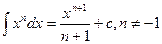
2. 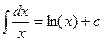
3. 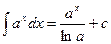
4. 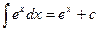
5. 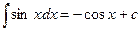
6. 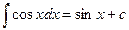
7. 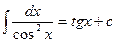
8. 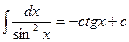
9. 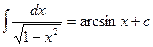
10. 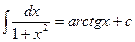
Доказательство таблицы легко провести по определению определённого интеграла.
Сделать самостоятельно.
Примеры.
1. 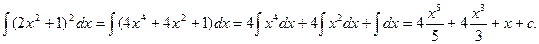
2.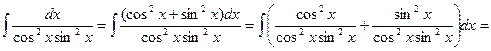
=