Линейная замена переменной.
Теорема.Если 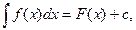 то
то 
Доказательство. Пусть ax+b=t (замена переменной)
dt=(ax+b)`dx dt=adx, dx=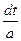 Тогда
Тогда

Примеры.
1.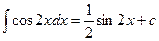 (Здесь вместо х стоит 2х a=2, b=0)
(Здесь вместо х стоит 2х a=2, b=0)
2.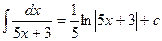 a=5, b=3
a=5, b=3
3. 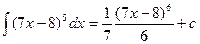 a=7, b=-8
a=7, b=-8
4. 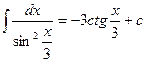 a=1/3, b=0
a=1/3, b=0
5.  a=2, b=-a
a=2, b=-a
6. 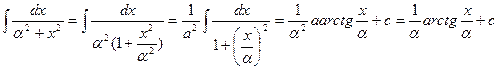 a=a, b=0
a=a, b=0
7. 
8. 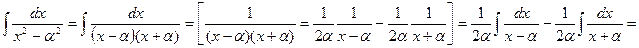
=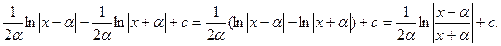
Расширим таблицу интегралов используя примеры 5-8.
1. 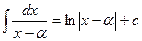
2.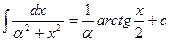
3. 
4. 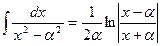
5. 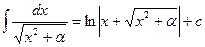 ; a¹0- проверить по определению неопределённого интеграла.
; a¹0- проверить по определению неопределённого интеграла.
Метод интегрирования по частям.
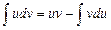 формула интегрирования по частям.
формула интегрирования по частям.
Примеры.
1. 
=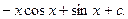
2. 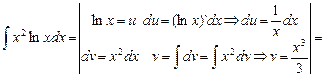
=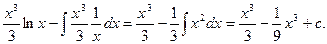
4. 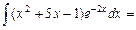
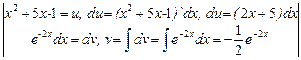 =
=
= -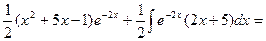 второй интеграл опять вычисляем по частям=
второй интеграл опять вычисляем по частям= 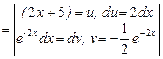 =
=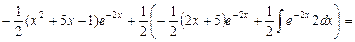
= -
=-
=e-2x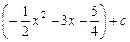 .
.
Интегрирование методом замены переменной при наличии производной.
1.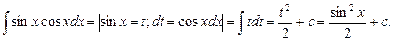
2. 
3.  ½lnx=t; dt=
½lnx=t; dt=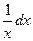 ½=
½=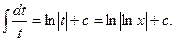
4. 
5. 
=1/3t2+c=1/3arctg23x+c.
6. 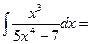 ½t=5x4-7;dt=20x3dx; x3dx=
½t=5x4-7;dt=20x3dx; x3dx=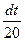 ½= =
½= =
Интегрирование выражений, содержащих квадратный трёхчлен Ax2+Bx+C.
1.  ½x2+6x-3=(x2+6x+9)-9-3=(x+3)2-12- выделение полного квадрата½=
½x2+6x-3=(x2+6x+9)-9-3=(x+3)2-12- выделение полного квадрата½=
=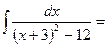 ½комбинируем теорему о линейной замене (вместо х стоит х+3, a=1, b=3)
½комбинируем теорему о линейной замене (вместо х стоит х+3, a=1, b=3)
с дополнительной таблицей 5.(a2=12, a=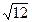 .½=
.½=
2. 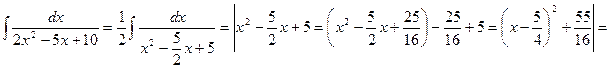
=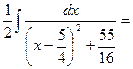 (применим дополнительную таблицу 2)
(применим дополнительную таблицу 2) 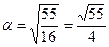
=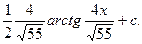
3. 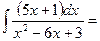 ½найдём производную от знаменателя (х2-6х+3)`=2x-6.
½найдём производную от знаменателя (х2-6х+3)`=2x-6.
преобразуем числитель так чтобы в нём появилась производная от знаменателя.
5х+1=5(х+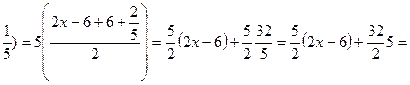
=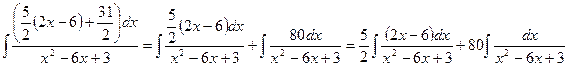
Вычислим отдельно первый интеграл
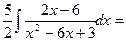 ½x2-6x+3=t; dt=(2x-6)dx½=
½x2-6x+3=t; dt=(2x-6)dx½=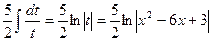
Вычислим второй интеграл как в примерах 1 и 2.
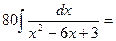

=80 тогда получаем
тогда получаем 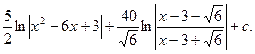
4. 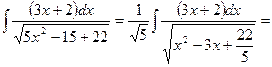 ½(х2-3х+22/5)`=2x-3; 3x+2=3(x+2/3)=
½(х2-3х+22/5)`=2x-3; 3x+2=3(x+2/3)=
=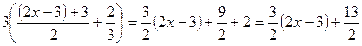 ½=
½= .
.
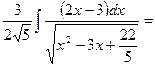 ½x2-3x+22/5=t; dt=(2x-3)dx½=
½x2-3x+22/5=t; dt=(2x-3)dx½=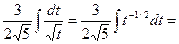
=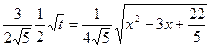
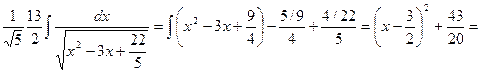
= ( дополнительная таблица формула 5)=
( дополнительная таблица формула 5)=
=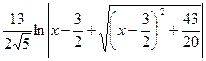 Итак получаем
Итак получаем
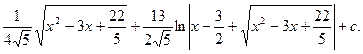
Определённый интеграл.
Определение. Определённым интегралом  от функции f(x) на отрезке [a,b], азовём число, равное F(b)-F(a), где F(x)-первообразная для f(x) на отрезке [a,b].
от функции f(x) на отрезке [a,b], азовём число, равное F(b)-F(a), где F(x)-первообразная для f(x) на отрезке [a,b].
Примеры.
1. 
2.
3.  ½x2=t, dt=2xdx; x=0Þ t=0 xdx=
½x2=t, dt=2xdx; x=0Þ t=0 xdx= ; x=
; x=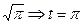 ½=
½=
=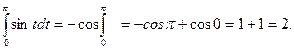
4. 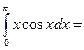 ½x=u du=dx, cosxdx=dv v=
½x=u du=dx, cosxdx=dv v=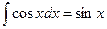 ½=
½=
=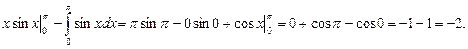
Вычисление площади криволинейной фигуры.
Пусть у=f1(x) и y=f2(x) непрерывные на [a,b] функции, f2(x)³f1(x) на [a,b], тогда площадь фигуры ограниченная линиями x=a, x=b, y=f2(x), y=f1(x) вычисляется по формуле







y

 y=f2(x)
y=f2(x)


 |
a b x
Пример. Вычислить площадь фигуры, ограниченной линиями у=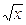 , у=х2, х=0, х=1.
, у=х2, х=0, х=1.






y=x2 S=
y=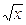 =
=
Несобственные интегралы.
Определение. Интеграл вида 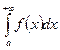 или
или 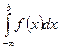 называется несобственным.
называется несобственным.
По определению 
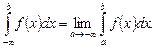
Примеры.
1. 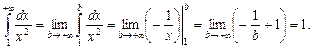
2. 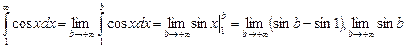 - не существует,
- не существует,
следовательно данный интеграл расходится.
3.  ½lnx=t; dt=
½lnx=t; dt=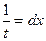 ; x=1 ln1=0Þt=0; x=b lnb=t½=
; x=1 ln1=0Þt=0; x=b lnb=t½=
b®+¥
=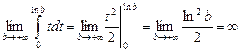 .
.
Следовательно, данный интеграл расходится.