Взаимное расположение прямой с плоскостью
1. Угол между прямой  с направляющим вектором
с направляющим вектором  и плоскостью
и плоскостью 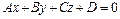 с нормальным вектором
с нормальным вектором  вычисляется по формуле
вычисляется по формуле
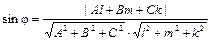 .
.
2. Условие параллельности прямой и плоскости: прямая  с направляющим вектором
с направляющим вектором  и плоскость
и плоскость 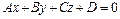 с нормальным вектором
с нормальным вектором  параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда
 .
.
3. Условия перпендикулярности прямой и плоскости: прямая  с направляющим вектором
с направляющим вектором  и плоскость
и плоскость 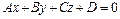 с нормальным вектором
с нормальным вектором  перпендикулярны тогда и только тогда, когда
перпендикулярны тогда и только тогда, когда
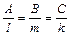 .
.
4. Условие принадлежности двух прямых одной плоскости: прямые  с направляющим вектором
с направляющим вектором  и
и  с направляющим вектором
с направляющим вектором  принадлежат плоскости тогда и только тогда, когда
принадлежат плоскости тогда и только тогда, когда
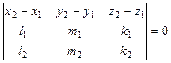 .
.
5. Условия принадлежности прямой плоскости: прямая  с направляющим вектором
с направляющим вектором  принадлежит плоскости
принадлежит плоскости 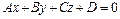 с нормальным вектором тогда и только тогда, когда выполняется
с нормальным вектором тогда и только тогда, когда выполняется

4.2. Контрольные задания
1. Даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее z1, z2, z3 через x1, x2, x3.
1. 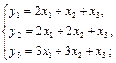
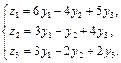
2. 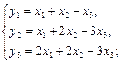
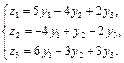
3. 

4. 

5. 
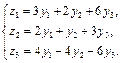
6. 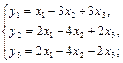

7. 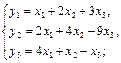
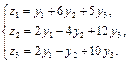
8. 
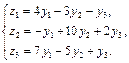
9. 

10. 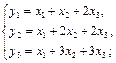

2. Дана система линейных уравнений. Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) с помощью обратной матрицы.
1.  2.
2. 
3. 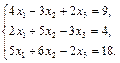 4.
4. 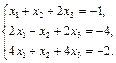
5. 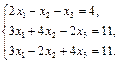 6.
6. 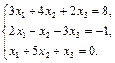
7. 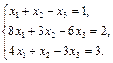 8.
8. 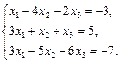
9. 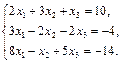 10.
10. 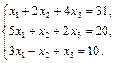
3. Даны вершины треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А (в радианах). Сделать чертеж.
1. A(1; 1), B(7; 4), C(4; 5). 2. A(1; 1), B(–5; 4), C(–2; 5).
3. A(–1; 1), B(5; 4), C(2; 5). 4. A(–1; 1), B(–7; 4), C(–4; 5).
5. A(1; –1), B(7; 2), C(4; 5). 6. A(1; –1), B(–5; 2), C(–2; 3).
7. A(–1; –1), B(5; 2), C(2; 3). 8. A(–1; –1), B(–7; 2), C(–4; 3).
9. A(0; 1), B(6; 4), C(3; 5). 10. A(1; 0), B(7; 3), C(4; 4).
4. Составить уравнение и построить линию, для каждой точки которой выполняется следующее условие:
1. Расстояние ее до точки F(–1; –2) равно расстоянию от прямой
x = –3;
2. Отношение расстояний до точки F(7; 0) и прямой x = 1 равно 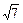 ;
;
3. Отношение расстояний до точки F(2; 0) и прямой x = 3 равно  ;
;
4. Расстояние ее до точки F(3; 3) равно расстоянию от прямой
x = –2;
5. Отношение расстояний до точки F(2; 0) и прямой 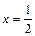 равно 2;
равно 2;
6. Отношение расстояний до точки F(–1; 0) и прямой x = –9 равно  ;
;
7. Расстояние ее до точки F(–3; 2) равно расстоянию от прямой x = 2;
8. Отношение расстояний до точки F(3; 0) и прямой x = 2 равно 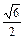 ;
;
9. Отношение расстояний до точки F(–4,5; 0) и прямой x = –8 равно 0,75;
10. Расстояние ее до точки F(1; 0) равно расстоянию от прямой x = 3.
5. Написать разложение вектора 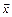 по векторам
по векторам  ,
,  ,
, 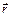 .
.
1. 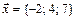 ,
,  ,
,  ,
,  .
.
2.  ,
, 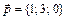 ,
,  ,
, 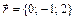 .
.
3.  ,
,  ,
, 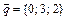 ,
, 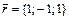 .
.
4. 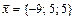 ,
,  ,
,  ,
, 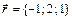 .
.
5. 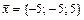 ,
, 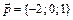 ,
,  ,
,  .
.
6.  ,
, 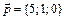 ,
, 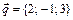 ,
, 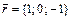 .
.
7.  ,
,  ,
, 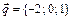 ,
, 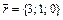 .
.
8. 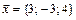 ,
, 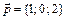 ,
,  ,
,  .
.
9.  ,
, 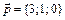 ,
,  ,
, 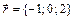 .
.
10.  ,
,  ,
, 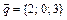 ,
,  .
.
6. Даны вершины пирамиды A1A2A3A4. Найти: 1) угол между ребрами A1A3 и A1A4; 2) площадь грани A1A2A3; 3) уравнение плоскости, содержащей грань A1A2A3; 4) уравнения высоты пирамиды, проведенной через вершину A4. Сделать схематический чертеж.
1. A1(2; 1; –4), A2(1; –2; 3), A3(1; –2; –3), A4(5; –2; 1).
2. A1(2; –1; 3), A2(–5; 1; 1), A3(0; 3; –4), A4(–1; –3; 4).
3. A1(5; 3; 2), A2(1; –8; 8), A3(4; –1; 2), A4(1; 4; –1).
4. A1(–2; 3; 4), A2(4; 2; –1), A3(2; –1; 4), A4(–1; –1; 1).
5. A1(4; –4; 0), A2(–5; 3; 2), A3(8; 0; 1), A4(2; 2; 3).
6. A1(–3; –4; 0), A2(0; –1; 3), A3(–6; 4; 2), A4(–3; 0; 3).
7. A1(0; 4; –4), A2(5; 1; –1), A3(–1; –1; 3), A4(0; –3; 7).
8. A1(0; –6; 3), A2(3; 3; –3), A3(–3; –5; 2), A4(–1; –4; 0).
9. A1(2; –1; –3), A2(0; 0; 0), A3(5; –1; –1), A4(–1; –1; 1).
10. A1(1; 5; 8), A2(–2; 1; 4), A3(3; –2; –3), A4(1; –1; 0).
4.3. Пример решения контрольной работы
Задание 1. Даны два линейных преобразования:
 и
и 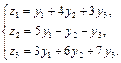
Средствами матричного исчисления найти преобразование, выражающее z1, z2, z3 через x1, x2, x3.
Решение. Первое преобразование определяется матрицей А, а второе – матрицей В, где
 ,
,  .
.
Искомое преобразование является произведением данных преобразований с матрицей
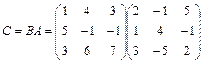 .
.
Перемножив матрицы В и А, получим матрицу
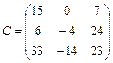 .
.
Следовательно, искомое преобразование таково:

Ответ: 
Задание 2. Дана система линейных уравнений  Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) с помощью обратной матрицы.
Доказать её совместность и решить двумя способами: 1) методом Гаусса; 2) с помощью обратной матрицы.
Решение. 1) Запишем расширенную матрицу В системы и найдем ранг матрицы В методом Гаусса, приводя к ступенчатому виду.
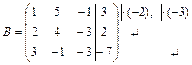 ~
~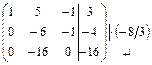 ~
~
~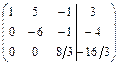 .
.
Так как ранг матрицы равен числу ненулевых строк, то r(B) = 3.
Основная матрица А системы, состоящая из коэффициентов системы имеет вид
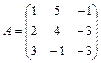 .
.
Рассуждая аналогично, получаем, что r(А) = 3.
Так как ранг основной матрицы равен рангу расширенной матрицы, то по теореме Кронекера-Капелли система совместна и имеет единственное решение.
Финальную матрицу В запишем в виде системы

и найдем ее решение. Из последнего уравнения  системы следует, что х3 = –2. Подставляя х3 = –2 во второе уравнение, найдем –6х2 + 2 = –4 или –6х2 = –6 или х2 = 1. Наконец, подставляя х2 = 1 и х3 = –2 в первое уравнение системы, получим х1 + 5 + 2 = 3 или х1 = –4.
системы следует, что х3 = –2. Подставляя х3 = –2 во второе уравнение, найдем –6х2 + 2 = –4 или –6х2 = –6 или х2 = 1. Наконец, подставляя х2 = 1 и х3 = –2 в первое уравнение системы, получим х1 + 5 + 2 = 3 или х1 = –4.
2) Обозначим
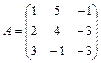 ,
,  ,
,  .
.
Вычислим определитель основной матрицы А системы по правилу треугольников

 .
.
Так как | A | ¹ 0, то матрица А невырожденная, и существует обратная матрица.
Вычислим обратную матрицу А–1 по формуле
 ,
,
где Аij – алгебраическое дополнение элемента аij матрицы А.
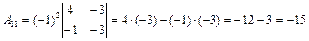 ,
,
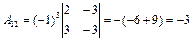 ,
,
 ,
,
 ,
,
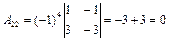 ,
,
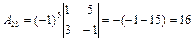 ,
,
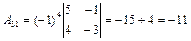 ,
,
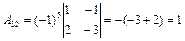 ,
,
 .
.
Таким образом, получим
 .
.
По формуле Х = А–1В находим решение системы в матричной форме
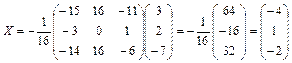 .
.
Используя определение равенства двух матриц, получаем
х1 = –4, х2 = 1, х3 = –2.
Ответ: х1 = –4, х2 = 1, х3 = –2.
Задание 3. Даны вершины А(–1; 0), В(5; 2), С(2; 4) треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А (в радианах). Сделать чертеж.
Решение. Изобразим заданный треугольник в декартовой прямоугольной системе координат (рис. 10).
1) Длину стороны АВ найдем, используя формулу расстояния между двумя точками на плоскости
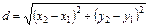 .
.
Подставляя в нее координаты точек А(–1; 0) и В(5; 2), окончательно получим
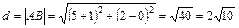 (ед.).
(ед.).
