Системы линейных уравнений

1. В общем случае система m линейных уравнений с n неизвестными имеет вид

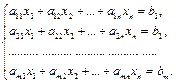(1)

Числа a_ij, где i = 1, 2, …, m, j = 1, 2, …, n, называются коэффициентами системы, переменные х₁, х₂, …, x_n, подлежащие определению, называются неизвестными, числа b₁, b₂, …, b_m называются свободными членами.

2. Совокупность n чисел a₁, a₂, …, a_n называется решением системы (1), если после замены неизвестных х₁, х₂, …, x_n, числами a₁, a₂, …, a_n соответственно каждое из уравнений системы превращается в верное числовое равенство.

3. Система (1) называется совместной, если она имеет хотя бы одно решение, и называется несовместной, если не имеет ни одного решения.

4. Совместная система (1) называется определенной, если она имеет единственное решение, и называется неопределенной, если у неё существуют, по крайней мере, два различных решения.

5. Пусть k – какое-нибудь натуральное число, не превосходящее m и n. Выделим в этой матрице любые k строк и k столбцов. Тогда элементы, стоящие на пересечении выделенных k строк и k столбцов, образуют квадратную матрицу порядка k. Определитель этой квадратной матрицы называется определителем, порождённым матрицей A, или минором k-го порядка матрицы A.

6. Рангом матрицы A называется число, равное наивысшему порядку миноров этой матрицы, отличных от нуля. Если каждый элемент матрицы равен нулю, то ранг такой матрицы считается равным нулю по определению. Ранг матрицы А обозначается символами r(A) или rang A.

7. Теорема Кронекера – Капелли. Для того чтобы система m линейных уравнений с n неизвестными вида (1) была совместной, необходимо и достаточно, чтобы ранг матрицы 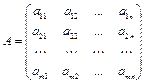системы был равен рангу расширенной матрицы 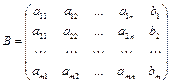, т. е.

r(A) = r(B).

Из теоремы следует, что если r(A) ¹ r(B), то система несовместна; если r(A) = r(B) = n, то система имеет единственное решение; если r(A) = r(B) < n, то система имеет бесчисленное множество решений.

8. Элементарными преобразованиями системы линейных уравнений называются следующие операции:

1) умножение какого-либо уравнения системы на число, отличное от нуля;

2) прибавление к одному уравнению другого уравнения, умноженного на произвольное число;

3) перестановка местами двух уравнений в системе.

При помощи элементарных преобразований мы можем значительно упростить заданную систему. Решив упрощенную систему, мы найдем тем самым и решение исходной системы.