Метод Гаусса

Метод Гаусса решения систем линейных уравнений состоит в том, что последовательным исключением неизвестных при помощи элементарных преобразований систему приводят к такому виду, чтобы матрица системы оказалась треугольной или трапециевидной. После этого решить систему не представляет труда.

Пусть задана произвольная система линейных уравнений (1). Будем считать, что a₁₁ ¹ 0 (в противном случае можно произвести перестановку уравнений). Исключим сначала неизвестное x₁ из всех уравнений системы (1), кроме первого. Для этого прежде всего разделим обе части первого уравнения на коэффициент a₁₁ ¹ 0; тогда получим новую систему, равносильную данной:

(2)

Умножим теперь первое уравнение системы (2) на –a₂₁ и сложим его почленно со вторым уравнением. Затем умножим первое уравнение системы (2) на –a₃₁ и сложим его с третьим уравнением и так далее. В результате получим новую систему, также равносильную данной:

(3)

Здесь штрихами отмечены коэффициенты при неизвестных и свободные члены, полученные при первом шаге исключения неизвестных по формулам

Допустим, что в системе (3) (в противном случае всегда можно изменить порядок следования уравнений или перенумеровать неизвестные). Разделим теперь второе уравнение системы (3) на коэффициент ; затем умножим второе уравнение полученной системы последовательно на 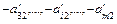и сложим поочередно с каждым соответствующим уравнением системы, кроме первого и второго. Тогда получим систему, равносильную системам (1), (2), (3):

(4)

Далее действия над уравнениями системы (4) будем продолжать аналогично. Если при этом появятся нулевые уравнения, т. е. равенства 0=0, их отбрасывают, поэтому можно считать, что в системе (4) таких уравнений нет. Процесс указанных равносильных преобразований над системой линейных уравнений называется процессом Гаусса.

В результате процесса Гаусса возможны следующие три случая.

1) Если появится уравнение 0 = b, где b ¹ 0, то исходная система несовместна, т. е. решений не имеет.

2) Если система приводится к треугольному виду, то она является определённой, т. е. решение системы существует и единственно.

3) Если система приводится к трапециевидной форме, то она является неопределённой, т. е. имеет бесчисленное множество решений.