Решение.

Задаем систему координат. Проекции на горизонтальную ось всех внешних сил (сил тяжести G_A, G_B, G_C, G_D, реакции опоры N), дей­ствующих на систему, равны нулю (рис. 11.2), а трения между приз­мой D и опорой по условию нет. Применим к системе следствие из теоремы о движении центра масс.

 

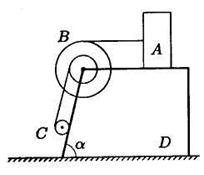
Рис. 11.1 Рис. 11.2

 

1. Абсолютное смещение тел А, В и С представляем как сумму от­носительного смещения, зависящего от величины S относительного смещения груза А, и неизвестного переносного смещения AD, равного абсолютному смещению призмы, относительно которой задавалось смещение S. Обозначаем абсолютные смещения координат центров масс тел системы Δ_А, Δ_B, Δ_C, Δ_D. Направление оси х определяет знаки смещений: налево с минусом, направо с плюсом. Предпола­гаем, что призма сместится направо. Перемещение центра цилиндра С относительно призмы и перемещение груза А связаны так же, как связаны их скорости.

Цилиндр С совершает плоское движение. Абсолютное смещение его центра в проекции на ось х равно Δ_D — S_C cos α, где S_C — сме­щение центра цилиндра вдоль наклонной поверхности призмы. Вы­разим S_C через S. Для этого свяжем скорости груза А и центра масс цилиндра С. Мгновенный центр скоростей цилиндра находится в точке касания призмы, поэтому скорость его центра масс относи­тельно призмы вдвое меньше скорости нити, накручиваемой на обод. Скорость груза А выражаем через угловую скорость блока:

 

.

 

Исключая отсюда , имеем связь скоростей: . Интег­рируя это соотношение при нулевых начальных значениях, получаем искомую зависимость: S_C =0,5Sr/R. Находим выражение абсолют­ных смещений всех тел через Δ_D, и S:

 

.

 

2. Подставляя абсолютные смещения, получаем уравнение

 

,

или

.

 

Призма D переместится вправо на 14.39 см.

 

Задача 11.3.2. Определить дав­ление на подшипник О, если груз 1 опускается с ускорением а₁ (рис. 11.3). Массы тел равны т₁, т₂, т₃, радиусы ступеней блока R и r. Массу нити и сопротивление движению не учитывать. Центр масс блока совпадает с точкой О.

Рис. 11.3

Решение. Определение дав­ления на подшипник О заменим определением реакции подшип­ника, так как эти силы имеют равные величины. Внешними си­лами, действующими на систему, являются силы тяжести и реакции подшип­ника 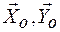. Для определения реакций подшипника воспользуемся теоремой о движении центра масс в проекциях на координатные оси

 

 

В рассматриваемом случае

 

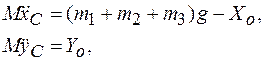
откуда

(11.10)

 

Таким образом, для определения реакций подшипника необхо­димо знать проекции ускорения центра масс системы на координат­ные оси.

По определению центра масс

 

,

 

где проекции ускорений центров масс тел системы на координатные оси

 

 

Здесь учтено, что 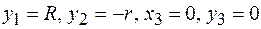; следовательно,

 

.

 

Подставляя последние формулы в (11.10), получаем

 

 

Таким образом, давление на подшипник О определяется по формуле

 

 

в которой слагаемое, подчеркнутое одной линией, равно статиче­скому давлению, а слагаемое, подчеркнутое двойной линией, опре­деляет дополнительное давление, зависящее от движения системы.

 

11.4.Задания Д – 11

 

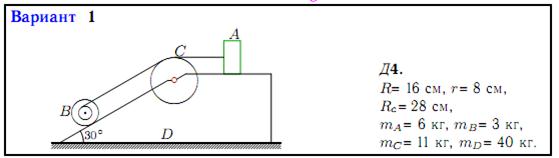
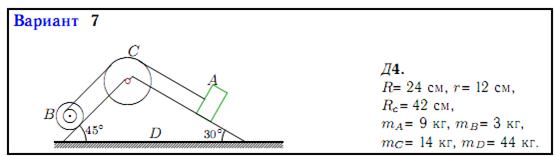
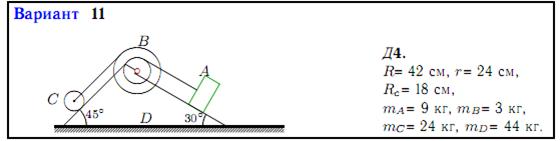
Механизм, состоящий из груза A, блока B (больший радиус R, меньший r) и цилиндра радиуса R_C, установлен на призме D, находящейся на горизонтальной плоскости. Трение между призмой и плоскостью отсутствует. Груз A получает перемещение S = 1 м относительно призмы вдоль ее поверхности влево или (в тех вариантах, где он висит) по вертикали вниз. Куда и на какое расстояние переместится призма?