Кинетическая энергия твердого тела при различном движении.

1. Поступательное движение

 

.

 

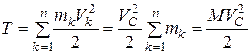2. Вращение тела вокруг неподвижной оси

,

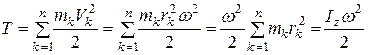где 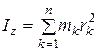- момент инерции тела относительно оси вращения.

 

3. Плоскопараллельное движение

 

,

 

где — момент инерции плоской фигуры относительно оси, проходящей через центр масс.

 

Теорема об изменении кинетической энергии механической системы имеет две формы: дифференциальную и конечную (инте­гральную).

Дифференциальная форма теоремы имеет вид

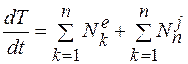, (12.2)

 

производная по времени от кинетической энергии системы равна сумме мощностей всех внешних и внутренних сил, действующих на точки системы.

Соотношение (12.2) можно записать в виде

 

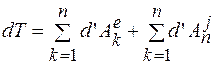, (12.3)

 

дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на точки системы.

Теорема об изменении кинетической энергии в конечной форме имеет вид

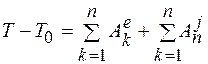. (12.4)

 

Изменение кинетической энергии на конечном перемещении системы из положения, в кото­ром кинетическая энергия равна Т_о, в положение, в котором кинети­ческая энергия равна Т, равно сумме работ всех внешних и внутрен­них сил системы на этом перемещении.

Практическое применение соотношений при решении задач ос­ложняется наличием в их правых частях членов, связанных с внут­ренними силами, которые, как правило, заранее неизвестны. Однако существует широкий класс систем, для которых упомянутые члены можно опустить: это системы, состоящие из совокупности абсолют­но твердых тел, скрепленных между собой идеальными связями (шарниры без трения, нерастяжимые и абсолютно гибкие нити и т.д). Для таких систем (их называют неизменяемыми)

,

 

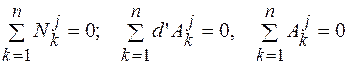и соотношения (12.2)—(12.4) записываются в виде

 

,

,

.

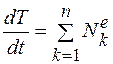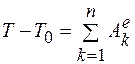Рассмотрим порядок составления дифференциального уравне­ния движения системы с одной степенью свободы с помощью тео­ремы об изменении кинетической энергии в дифференциальной форме:

1. Убедиться в том, что система имеет одну степень свободы.

2. Выбрать координату, относительно которой будет состав­ляться дифференциальное уравнение движения: это, как правило, либо линейная величина (назовем ее для конкретности х), опреде­ляющая положение тела, движущегося поступательно, либо угловая величина (назовем ее 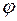, определяющая положение тела, вращаю­щегося вокруг неподвижной оси.

3. Записать теорему об изменении кинетической энергии.

4. Вычислить кинетическую энергию системы как сумму кине­тических энергий тел, входящих в ее состав. На расчетной схеме показать все кинематические характеристики, от которых зависит ки­нетическая энергия системы.

5. Представить кинетическую энергию системы в виде 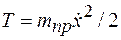, если за координату принята линейная величина, или в виде 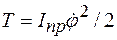, если за координату принята угловая величина. Для этого скорости, входящие в выражение кинетической энергии системы, следует выразить либо через 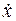, либо через 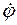. Величины 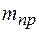и 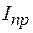называют соответственно приведенной массой и приведен­ным моментом инерции системы.

6. Вычислить производную по времени от кинетической энергии.

7. Изобразить на расчетной схеме внешние силы, действующие на систему. Вычислить сумму мощностей внешних сил.

8. Представить сумму мощностей внешних сил в виде , если за координату принята линейная величина, или в виде 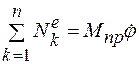, если за координату принята угловая величина.

9. Сформировать дифференциальное уравнение движения. Для этого следует, согласно п. 3, приравнять правые части выражений, полученных в п. 6 и 8, и провести сокращение на производную по времени от координаты, присутствующую в качестве множителя в обеих частях уравнения.

Если решается вторая задача динамики, т.е. определяется за­кон движения системы, то далее следует выполнить следующие действия:

10. Сформулировать начальные условия движения системы.

11. Построить общее решение дифференциального уравнения движения.

12. Определить по начальным условиям постоянные интегриро­вания.

13. Подставив значения постоянных интегрирования в общее решение дифференциального уравнения, найти закон движения системы.

Б. Конечная форма теоремы

Рассмотрим порядок решения задачи, предполагая, что система приходит в движение из состояния покоя:

1. Убедиться в том, что система имеет одну степень свободы.

2. Выбрать координату, с помощью которой будет определяться положение системы, связав выбор с целью задачи: если, например, определяется зависимость скорости тела, совершающего прямоли­нейное поступательное движение, то в качестве координаты прини­мается перемещение тела; если же определяется зависимость угло­вой скорости тела, вращающегося вокруг неподвижной, то в качест­ве координаты принимается угол поворота тела. Координаты следует отсчитывать от начального положения.

3. Записать теорему об изменении кинетической энергии в конечной фор­ме, положив Т₀ =0.

4. Изобразить на рисунке систему в конечном положении. Вы­числить кинетическую энергию системы в конечном положении как сумму кинетических энергий тел, входящих в ее состав. На расчет­ной схеме показать все кинематические характеристики, от которых зависит кинетическая энергия системы.

5. Представить кинетическую энергию системы в виде 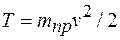, если определяется зависимость v=v(x), или в виде 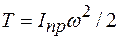, если определяется зависимость . Для этого ско­рости, входящие в выражение кинетической энергии системы, сле­дует выразить либо через v, либо через .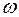

6. Изобразить на расчетной схеме внешние силы, действующие на систему; вычислить сумму работ внешних сил, представив ее либо в виде 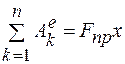, либо в виде .

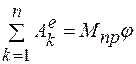7. Приравняв, согласно п. 3, правые части выражений, получен­ных в п. 5 и 6, определить из полученного соотношения искомую зависимость.