Базовые понятия теории и методические рекомендации по решению задач
Дифференциальные уравнения движения голономной механической системы в обобщенных координатах, или уравнения Лагранжа второго рода, имеют вид:
 (14.1)
(14.1)
где Т- кинетическая энергия системы; 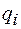 - обобщенные координаты;
- обобщенные координаты; 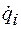 - обобщенные скорости;
- обобщенные скорости; 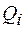 - обобщенные силы; s - число степеней свободы системы.
- обобщенные силы; s - число степеней свободы системы.
При составлении уравнений Лагранжа второго рода обычно используются различные способы вычисления обобщенных сил.
Первый способ основан на определении обобщенной силы 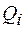 как коэффициента при вариации
как коэффициента при вариации 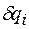 , соответствующей обобщенной координаты
, соответствующей обобщенной координаты 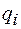 в выражении возможной работы активных сил системы:
в выражении возможной работы активных сил системы:
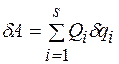 .
.
Для вычисления обобщенной силы 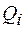 , системе сообщается возможное перемещение
, системе сообщается возможное перемещение 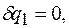
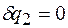 ,...,
,...,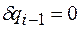 ,
, ,…,
,…,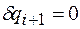 , ...,
, ...,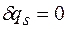 , на котором изменяется только обобщенная координата
, на котором изменяется только обобщенная координата 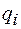 при неизменных других координатах и определяется возможная работа активных сил на этом перемещении:
при неизменных других координатах и определяется возможная работа активных сил на этом перемещении:
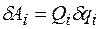 ,
,
откуда
 .
.
Второй способ пригоден в случае, если система находится в потенциальном поле сил:
 ,
,
причем, потенциальная энергия системы должна быть выражена как функция обобщенных координат.
Основное назначение уравнений Лагранжа второго рода - составление дифференциальных уравнений движения механической системы, подчиненной идеальным удерживающим голономным связям. Если среди связей, наложенных на систему, имеются неидеальные, то реакции этих связей следует ввести в число активных сил.
Составление дифференциальных уравнений движения с помощью уравнений Лагранжа второго рода рекомендуется проводить в следующем порядке:
1. Определить число степеней свободы и выбрать обобщенные координаты.
2. Записать уравнения Лагранжа (14.1) с учетом выбранных обобщенных координат.
3. Вычислить кинетическую энергию системы как функцию обобщенных координат и обобщенных скоростей.
4. Найти производные от кинетической энергии, входящие в левую часть уравнений Лагранжа.
5. Найти обобщенные силы.
6. Подставить результаты, полученные в п. 4 и 5, в уравнения п.2. Если в задаче требуется найти уравнения движения системы, то следует проинтегрировать полученную систему дифференциальных уравнений движения, определив постоянные интегрирования по начальным условиям.