Рекомендации по решению задач
Моментом силы 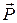 относительно точки Оназывается алгебраическая величина равная произведению модуля силы на ее плечо d относительно этой точки(рис.2.1)
относительно точки Оназывается алгебраическая величина равная произведению модуля силы на ее плечо d относительно этой точки(рис.2.1)
 .
.
Плечом силы относительно точки называется кратчайшее расстояние от этой точки до линии действия силы. В международной системе единиц СИ момент силы измеряется в ньютон-метрах (Н∙м).
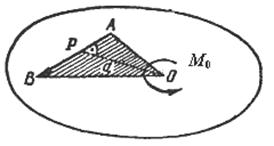
Рис. 2.1
Момент силы относительно точки считается положительным, если сила 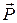 стремится повернуть плоскость чертежа вокруг точки О в сторону, противоположную вращению часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки. Момент силы относительно точки О равен нулю, если линия действия силы проходит через эту точку, т. е. d=0.
стремится повернуть плоскость чертежа вокруг точки О в сторону, противоположную вращению часовой стрелки, и отрицательным, если в сторону вращения часовой стрелки. Момент силы относительно точки О равен нулю, если линия действия силы проходит через эту точку, т. е. d=0.
При переносе точки приложения силы вдоль линии ее действия момент силы относительно данной точки не изменяется.
При решении задач полезно знать теорему Вариньона о моменте равнодействующей плоской системы сил.
Момент равнодействующей силы относительно любой точки на плоскости равен алгебраической сумме моментов составляющих сил относительно той же точки.
 .
.
Система двух равных по модулю, параллельных и противоположно направленных сил 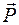 и
и  называется парой сил. Плоскость Q, в которой находятся линии действия сил
называется парой сил. Плоскость Q, в которой находятся линии действия сил 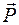 и
и  , называется плоскостью действия пары сил (рис. 2.2).
, называется плоскостью действия пары сил (рис. 2.2).
Кратчайшее расстояние d между линиями действия сил, составляющих пару, называется плечом пары сил.

Рис. 2.2
Пара сил не имеет равнодействующей и является такой системой сил, которую нельзя упростить. Под действием пары сил твердое тело совершает вращение. Количественной характеристикой действия пары сил на твердое тело, указывающей направление вращения тела под действием пары, является алгебраический момент пары.
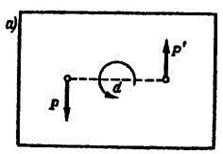



Рис. 2.3
Алгебраическим моментом пары сил называется взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил:
 .
.
Момент пары сил имеет знак плюс, если пара стремится вращать тело против часовой стрелки (рис. 2.3), и выражается в ньютон-метрах (Н∙м).
Пару сил, приложенную к твердому телу, можно охарактеризовать плоскостью действия, моментом пары сил и направлением вращения пары. Все эти характеристики пары сил в пространстве можно выразить одной величиной – векторным моментом пары сил.
Вектор момента 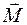 пары
пары  направляют перпендикулярно плоскости действия пары сил в такую сторону, чтобы, смотря навстречу этому вектору, видеть пару сил стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки (рис. 2.4).
направляют перпендикулярно плоскости действия пары сил в такую сторону, чтобы, смотря навстречу этому вектору, видеть пару сил стремящейся вращать плоскость ее действия в сторону, обратную вращению часовой стрелки (рис. 2.4).

Рис. 2.4
Числовое значение вектора момента пары сил совпадает с модулем алгебраического момента пары сил
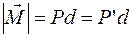 ,
,
где d – плечо пары сил.
Свойства пар сил:
1.Алгебраическая сумма моментов сил, составляющих пару, относительно произвольной точки плоскости не зависит от выбора этой точки и равна моменту пары.
2. Не нарушая состояния твердого тела, пару сил можно переносить в плоскости ее действия.
3. Пары сил, лежащие в одной плоскости, эквивалентны, если их моменты численно равны и одинаковы по знаку.
Это значит, что, не нарушая состояния твердого тела, можно изменять величину плеча либо величину силы, сохраняя при этом неизменным момент пары сил.
Силу 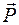 , не изменяя ее действия на твердое тело, можно перенести из точки ее приложения в любой центр приведения О, приложив при этом к телу пару сил с моментом
, не изменяя ее действия на твердое тело, можно перенести из точки ее приложения в любой центр приведения О, приложив при этом к телу пару сил с моментом 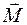 , геометрически равным моменту
, геометрически равным моменту  этой силы относительно центра приведения.
этой силы относительно центра приведения.
Плоская произвольная система сил приводится к главному вектору  и главному моменту
и главному моменту  . Для равновесия плоской произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил равнялись нулю.
. Для равновесия плоской произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил равнялись нулю.
Условия равновесия в векторной форме:
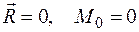 .
.
Для произвольной плоской системы сил можно составить три уравнения равновесия.
Первая форма уравнений равновесия:
1.  .
.
2.  .
.
3.  .
.
Третье уравнение составляют относительно произвольной точки. Лучше всего брать точку, в которой имеется больше неизвестных реакций.
Вторая форма уравнений равновесия:
1.  .
.
2. 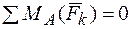 .
.
3.  .
.
При использовании второй формы уравнений равновесия необходимо, чтобы ось х не была перпендикулярна прямой АВ.
Третья форма уравнений равновесия:
1. 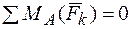 .
.
2.  .
.
3.  .
.
При использовании третьей формы уравнений равновесия необходимо, чтобы точки А, В, С не лежали на одной прямой.