Применение производной
26. Если на некотором промежутке 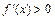 , то на этом промежутке функция
, то на этом промежутке функция 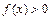 возрастает; если
возрастает; если 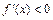 , то функция убывает.
, то функция убывает.
27. Если функция 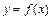 непрерывна в точке
непрерывна в точке 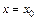 и в левой ее окрестности
и в левой ее окрестности 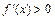 , а в правой
, а в правой 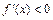 , то в точке
, то в точке 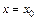 функция имеет максимум; если в левой окрестности
функция имеет максимум; если в левой окрестности 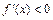 , а в правой
, а в правой 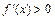 , то в точке
, то в точке 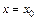 функция имеет минимум.
функция имеет минимум.
28. Если на некотором промежутке 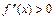 , то на этом промежутке функция
, то на этом промежутке функция  вогнута; если
вогнута; если  , то функция выпукла.
, то функция выпукла.
29. Если функция 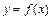 непрерывна в точке
непрерывна в точке 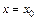 и при переходе через точку вторая производная меняет знак, то точка
и при переходе через точку вторая производная меняет знак, то точка 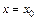 – точка перегиба.
– точка перегиба.
30. Для нахождения наибольшего или наименьшего значения функции 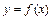 на отрезке
на отрезке 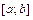 нужно:
нужно:
а) найти критические точки – точки, в которых производная функции 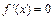 , не существует или равна бесконечности;
, не существует или равна бесконечности;
б) найти значения функции в критических точках, принадлежащие отрезку 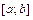 и на концах отрезка;
и на концах отрезка;
в) выбрать среди полученных чисел наибольшее или наименьшее.
31. Для исследования функции 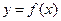 и построения ее графика пользуются следующей схемой:
и построения ее графика пользуются следующей схемой:
а) определяется область определения функции, находятся точки разрыва, определяется их характер, находятся вертикальные асимптоты, если они есть;
б) проверяется четность, нечетность, периодичность графика, поведение его при 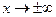 (или на границах области определения, если она ограничена); определяется наличие невертикальных асимптот вида
(или на границах области определения, если она ограничена); определяется наличие невертикальных асимптот вида 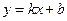 , для чего числа k и b находятся по формулам:
, для чего числа k и b находятся по формулам: 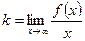 ,
, 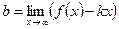 , если оба эти предела существуют и конечны;
, если оба эти предела существуют и конечны;
в) находится производная 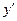 , определяются интервалы возрастания
, определяются интервалы возрастания  , убывания
, убывания 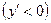 и критические точки (
и критические точки ( или не существует) функции, находятся экстремумы;
или не существует) функции, находятся экстремумы;
г) находится вторая производная 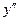 , определяются интервалы выпуклости вверх
, определяются интервалы выпуклости вверх 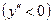 , выпуклости вниз
, выпуклости вниз 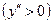 и точки перегиба графика;
и точки перегиба графика;
д) если необходимо, находятся дополнительные точки.
Сведя всю полученную информацию в таблицу, строят график функции 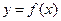 .
.