Касательная плоскость и нормаль к поверхности
4. Частные производные 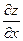 ,
, 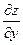 функции двух переменных
функции двух переменных  находятся по обычным правилам и формулам дифференцирования по каждой из переменной при фиксированном значении второй переменной. Например:
находятся по обычным правилам и формулам дифференцирования по каждой из переменной при фиксированном значении второй переменной. Например: 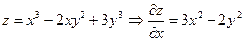 ;
;  .
.
5. Если поверхность задана явно функцией  , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 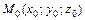 :
: 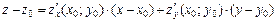 ; уравнение нормали в точке
; уравнение нормали в точке 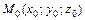 :
: 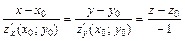 .
.
6. Если поверхность задана неявно уравнением 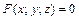 , то уравнение касательной плоскости в точке
, то уравнение касательной плоскости в точке 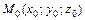 :
: 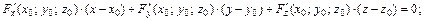 уравнение нормали в точке
уравнение нормали в точке 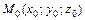 :
: 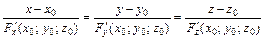 .
.
7. Полный дифференциал функции  находится по формуле:
находится по формуле: 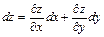 . Дифференциал второго порядка равен:
. Дифференциал второго порядка равен: 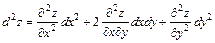 .
.
8. Если дифференциалы 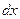 и
и  независимых переменных достаточно малы, дифференциал функции приближенно равен ее приращению:
независимых переменных достаточно малы, дифференциал функции приближенно равен ее приращению: 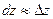 . Отсюда следует, что приближенное значение
. Отсюда следует, что приближенное значение 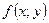 в точке
в точке 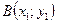 можно найти по формуле:
можно найти по формуле: 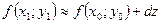 , где
, где  ,
,  , а значения частных производных вычисляются в точке
, а значения частных производных вычисляются в точке 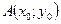 . Если обозначить
. Если обозначить 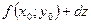 через
через 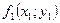 , то абсолютная погрешность
, то абсолютная погрешность  , относительная погрешность
, относительная погрешность  .
.
9. Производная функции  по направлению вектора
по направлению вектора  вычисляется по формуле:
вычисляется по формуле:  .
.
10. Градиент функции  есть вектор с координатами
есть вектор с координатами 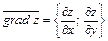 .
.