Определенный интеграл

1. Пусть на отрезке [a; b] задана функция f(x). Произвольным образом разобьем отрезок [a; b] на n частей точками a = x₀ <x₁ < x₂ < … <
< x_k–1 < x_k < … <x_n = b. Обозначим через Dx_k = xk – x_k–1 – длину k-го отрезка. На каждом отрезке [x_k–1; x_k] возьмем произвольно точку x_k и вычислим в ней значение функции f(x_k). Найдем все произведения f(x_k)Dx_k и составим интегральную сумму 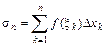. Если существует конечный предел интегральной суммы при n → ¥, не зависящий ни от способа разбиения отрезка [a; b] на части, ни от выбора точек x_k, то этот предел называется определенным интегралом от функции f(x) на отрезке [a; b] и обозначается символом .

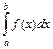2. – формула Ньютона-Лейбница.

3. – формула интегрирования по частям.

4. Геометрический смысл определенного интеграла: интеграл 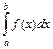численно равен площади криволинейной трапеции, ограниченной слева и справа прямыми и , осью 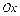и сверху графиком функции 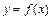(рис. 8).

 

 

 

Рис. 8 Рис. 9