Гауссовская случайная величина
Гауссовская (нормальная) СВ  имеет плотность вероятности
имеет плотность вероятности
 . (15)
. (15)
Здесь 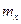 – среднее значение,
– среднее значение, 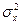 – дисперсия СВ
– дисперсия СВ  . Используя метод обратных функций, можно показать, что значение СВ
. Используя метод обратных функций, можно показать, что значение СВ  вычисляется по формуле
вычисляется по формуле
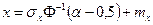 ,
,
где  – обратная функция по отношению к функции Лапласа
– обратная функция по отношению к функции Лапласа  , определенной выражением (7).
, определенной выражением (7).
Однако этот алгоритм на практике не применяют из-за больших затрат машинного времени. Это связано с тем, что при использовании ММК необходимо получать достаточно много значений СВ для вычисления результата с приемлемой точностью. Поэтому распространен другой алгоритм, позволяющий получать сразу два независимых значения гауссовской СВ 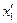 и
и 
с нулевыми средними и  :
:
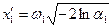
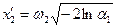
где 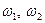 − координаты изотропного вектора
− координаты изотропного вектора  на плоскости. Это означает, что точка
на плоскости. Это означает, что точка 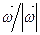 имеет равномерное распределение на окружности с единичным радиусом. Моделирование
имеет равномерное распределение на окружности с единичным радиусом. Моделирование 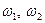 :
:
1) 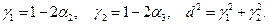
2) если 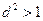 , то повторяем 1) и т. д., иначе
, то повторяем 1) и т. д., иначе
3) 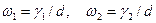 .
.
Заданные значения 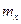 и
и  можно учесть с помощью линейного преобразования
можно учесть с помощью линейного преобразования
 . (16)
. (16)
Другой способ моделирования гауссовской СВ основан на центральной предельной теореме, согласно которой сумма большого числа независимых СВ имеет приближенно гауссовское распределение. Чем больше слагаемых, тем точнее аппроксимация распределения суммы гауссовской плотностью вероятности. Например, сумма
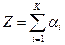
уже при значении 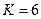 с хорошей степенью точности может считаться гауссовской СВ, пригодной для решения многих прикладных задач. Так как
с хорошей степенью точности может считаться гауссовской СВ, пригодной для решения многих прикладных задач. Так как  и
и 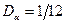 , то СВ
, то СВ  необходимо пронормировать
необходимо пронормировать
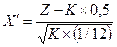 . (17)
. (17)
В результате получим СВ 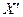 с нулевым средним и единичной дисперсией. Далее необходимо выполнить линейное преобразование (16) для перехода к СВ
с нулевым средним и единичной дисперсией. Далее необходимо выполнить линейное преобразование (16) для перехода к СВ  с заданными значениями среднего и дисперсии.
с заданными значениями среднего и дисперсии.