Определение.

Если булева алгебра M - двухэлементна (т. е. содержит только Ë и Î), то булевы функции называются двоичными функциями.

Если в двухэлементной булевой алгебре элементы Ë и Î интерпретировать как "включено" и "выключено", то двоичные функции называются переключательными функциями. При такой интерпретации Ë и Î обозначаются соответственно через 1 и 0.

Если M = {И, Л} - булева алгебра значений истинности, то булевы функции являются функциями истинности или функциями логики высказываний.

Переключательные функции одной переменной имеют вид

f: {0,1} à {0,1},

и может быть только четыре различных одноместных переключательных функций:

0: x à 0;

1: x à 1;

id : x à x , тождественная функция;

neg : x à Øx, функция отрицания.

Всякую переключательную функцию от n переменных можно задать таблицей из 2ⁿ строк, в которой в каждой строке записывают одну из оценок списка переменных, принимающих значение 0 или 1. Например, для n=3 переключательную функцию можно задать табл. 9

 

Таблица 9

X1	X2	X3	f(X1,X2,X3)
			f(1,1,1)
			f(1,1,0)
			f(1,0,1)
			f(1,0,0)
			f(0,1,1)
			f(0,1,0)
			f(0,0,1)
			f(0,0,0)

 

Так как длина каждого столбца равна 2ⁿ, а различных столбцов из 0 и 1 длины 2ⁿ имеется 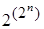, то существует точно 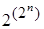переключательных функций от n переменных. В частности, при n=2 имеем 16 различных переключательных функций.

Вопрос: Нельзя ли свести все переключательные функции к какому-нибудь меньшему числу "базисных" переключательных функций?

Ответ: это возможно. Например, можно все переключательные функции представить как композицию только трех функций:

(двуместная конъюнкция) Ù : (x₁, x₂) à x₁Ù x₂ ;

(двуместная дизъюнкция) Ú : (x₁, x₂) à x₁Úx₂;

(одноместная функция отрицания) Ø : x à Øх.

Лемма 3.1. Для всякой n-местной переключательной функции f выполняется соотношение

f(a₁, a₂,…, a_i-1, a_i, a_i+1,…, a_n) =

(a_iÙf(a₁, a₂,…, a_i-1, 1, a_i+1,…, a_n)Ú (Øa_iÙf(a₁, a₂,…, a_i-1, 0, a_i+1,…, a_n).

Для доказательства рассмотрим два случая.

Пусть a_i=1, тогда Øa_i=0. Правая часть доказываемого соотношения равна (1Ùf(a₁, a₂,…, a_i-1, 1, a_i+1,…, a_n)Ú (0Ùf(a₁, a₂,…, a_i-1, 0, a_i+1,…, a_n). Первый член в дизъюнкции равен f(a₁, a₂,…, a_i-1, 1, a_i+1,…, a_n), а второй 0. Следовательно, правая часть равна f(a₁, a₂,…, a_i-1, 1, a_i+1,…, a_n), но точно такое же значение имеет левая часть.

Пусть a_i=0. Совершенно аналогично получаем, что правая часть равна f(a₁, a₂,…, a_i-1, 0, a_i+1,…, a_n).

Эта лемма позволяет "выносить" переменную a_i за знак переключательной функции. Последовательным применением леммы к a₁, a₂,…, a_n устанавливается

Теорема 3.1 (о булевой нормальной форме). Каждую переключательную функцию можно однозначно представить в следующей (дизъюнктивной) нормальной форме:

f(a₁, a₂,…, a_n) =

(a₁Ùa₂Ù…Ùa_n-1Ùa_nÙf(1,1,…,1,1))

Ú(Ø a₁Ùa₂Ù…Ùa_n-1Ùa_nÙf(0,1,…,1,1))

Ú( a₁ÙØa₂Ù…Ùa_n-1Ùa_nÙf(1,0,…,1,1))

….

Ú( Øa₁ÙØa₂Ù…ÙØa_n-1Ùa_nÙf(0,0,…,0,1))

Ú( Øa₁ÙØa₂Ù…ÙØa_n-1ÙØa_nÙf(0,0,…,0,0)).

Если f(a₁, a₂, …, a_n-1, a_n)=0, то соответствующий член, разумеется, выпадает из представления. Таким образом, всякая переключательная функция представима в виде дизъюнкции k, 0 £ k £ 2^k, членов - так называемых совершенных конъюнкций, каждая совершенная конъюнкция - это n-местная конъюнкция, у которых все аргументы - либо сами переменные, либо их отрицания.

Пример 3.1. Переключательную функцию с таблицей значений

 

a1
a2
a3
f(a1,a2,a3)

 

можно представить в виде

f(a₁,a₂,a₃) = (a₁Ùa₂Ùa₃)Ú(Øa₁ÙØa₂Ùa₃)Ú(Øa₁Ùa₂ÙØa₃)Ú(a₁ÙØa₂ÙØa₃).

Всего имеется 16 двуместных переключательных функций. Они распадаются на следующие группы:

Функция без совершенных конъюнкций

f(x₁,x₂) = 0

Функция со всеми четырьмя совершенными конъюнкциями

f(x₁,x₂) = (x₁Ùx₂)Ú(x₁ÙØx₂)Ú(Øx₁Ùx₂)Ú(Øx₁ÙØx₂) = 1

Четыре функции по одной совершенной конъюнкции

x₁Ùx₂ - конъюнкция

Øx₁ÙØx₂ - функция Пирса

x₁ÙØx₂ = x₁x₂

Øx₁Ùx₂ = x₂x₁

Четыре функции по три совершенных конъюнкции

x₁Úx₂ = (x₁Ùx₂)Ú(x₁ÙØx₂)Ú(Øx₁Ùx₂) - дизъюнкция

x₁|x₂ = (x₁ÙØx₂)Ú(Øx₁Ùx₂)Ú(Øx₁ÙØx₂) - штрих Шеффера

x₁ É x₂ = (x₁Ùx₂)Ú(Øx₁Ùx₂)Ú(Øx₁ÙØx₂)

x₂ É x₁ = (x₁Ùx₂)Ú(x₁ÙØx₂)Ú(Øx₁ÙØx₂)

Шесть функций по две совершенных конъюнкции

x₁ ~ x₂ = (x₁Ùx₂)Ú (Øx₁ÙØx₂) - эквивалентность

x₁ + x₂ = (x₁ÙØx₂)Ú(Øx₁Ùx₂) -симметрическая разность

(x₁Ùx₂)Ú(x₁ÙØx₂)

(Øx₁Ùx₂)Ú(Øx₁ÙØx₂)

(x₁Ùx₂)Ú(Øx₁Ùx₂)

(x₁ÙØx₂)Ú(Øx₁ÙØx₂)

Вопрос о тождественности двух переключательных функций можно решить, приведя их обоих к совершенной дизъюнктивной нормальной форме или преобразуя булевы выражения по законам булевой алгебры.