Переключательные элементы

Пусть имеется "черный ящик" - некоторое устройство, внутренняя структура которого нас не интересует, а известно лишь, что оно имеет n упорядоченных "входов" (например, занумерованных числами от 1 до n) и

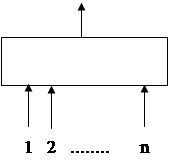один "выход" (рис. 3).

Рис. 3 "Черный ящик"

На каждый из входов могут подаваться два сигнала (например, отсутствие электрического тока или наличие его), которые мы условимся обозначать символами 0 и 1, и при каждом наборе сигналов на входах однозначно определяется сигнал на выходе. Такое устройство назовем переключательным элементом. Ясно, что каждому переключательному элементу соответствует переключательная функция f(x₁, x₂,…, x_n), которая строится следующим образом: входу с номером i (1 £ i £ n) ставится в соответствие переменная x_i и каждому (двоичному) набору значений этих переменных отвечает величина f(x₁, x₂,…, x_n), равная 0 или 1 в зависимости от того, какой сигнал возникает на выходе при подаче на входы переключательного элемента.

Если у нас имеется несколько переключательных элементов, то из них можно получать новые сложные переключательные элементы следующим образом. Один из входов одного переключательного элемента можно соединить с выходом другого переключательного элемента (рис. 4).

Рис. 4 Соединение "выход-вход"

Возникающее при этом устройство можно считать новым переключательным элементом, выходом которого является выход первого элемента (f), а входами все оставшиеся свободными входы первого элемента и входы второго элемента (g).

При таком соединении новому сложному переключательному элементу соответствует переключательная функция, полученная в результате суперпозиции исходных функций. Так, например, для элемента на рис. 4 имеем

h(x₁, y_1, y₂, x₃) = f(x₁, g(y₁, y₂),x₃).

Кроме этой операции можно отождествлять входы функционального элемента (рис. 5). При этом возникает новый переключательный элемент, у которого тот же выход и те же входы, за исключением отождествленных, которые теперь считаются одним входом. Для этого элемента соответствующая переключательная функция строится из первоначальной:

h(x₁, x₂, x₃) = f(x₁, x₂, x₂, x₂, x₃).

 

Рис. 5 Соединение "отождествление входов"

 

Можно использовать несколько соединений указанных выше двух типов. В этом случае получается сложный переключательный элемент или может получиться более сложное соединение, когда отождествляются некоторые входы различных переключательных элементов (рис. 6). В последнем случае такое соединение называется переключательной (комбинационной схемой).

Рис. 6 Комбинационная схема

Комбинационным схемам соответствует уже несколько переключательных функций (своя для каждого внешнего выхода), составленных с помощью суперпозиции. Для рис.6 получаем две переключательные функции {h, t}:

h(x₁, x₂, x₃, x₄, x₅, x₆) = f(x₁, g(x₂, x₃), x₄),

t(x₁, x₂, x₃, x₄, x₅, x₆) = p(x₄, x₅, x₅, x₅, x₆).

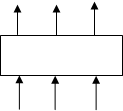Комбинационная схема изображается уже черным ящиком с несколькими выходами (рис. 7)

Рис. 7 Комбинационная схема

Символические изображения переключательных функций

Для трех переключательных функций: отрицания, конъюнкции и дизъюнкции - вместо прямоугольника используют три особых символических изображения (рис.8). Соответствующие переключательные элементы называются НЕ-элементом, И-элементом и ИЛИ-элементом; о них говорят как о логических элементах.

Символическое изображение
Формула	c = aÙb	c = aÚb	c = Øa
Название	И-элемент	ИЛИ-элемент	НЕ-элемент

Рис.8. Символические изображения для конъюнкции,

дизъюнкции и отрицания

Применение основных операций к переключательным функциям реализуется посредством соответствующего соединения символических изображений. Таким образом, возникают комбинационные схемы (в том числе и со многими выходами), построенные лишь из конъюнкции, дизъюнкции и отрицания. Вместо отрицания на входе конъюнкции или дизъюнкции ставят просто жирную "точку отрицания"; это дает такие картинки, как, например, на рис. 10.

Закон ассоциативности отражает возможность снабжать символические изображения логических элементов более чем двумя входами (рис. 9).

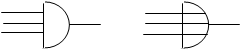Рис.9. И- и ИЛИ-элементы

со многими входами

Рис.10. Символическое изображение функции

Пирса: Ø(aÚb) = ØaÙØb

Пример: полусумматор

Для поразрядного сложения двух двоичных закодированных чисел применяется комбинационная схема, называемая полусумматором, с двумя

перестановочными входами a, b и двумя выходами s и u

s = a + b, u = aÙb.

На рис. 11 представлены две реализации полусумматора, для правой реализации использовано преобразование

a + b = Ø((aÙb)ÚØ(aÚb)).

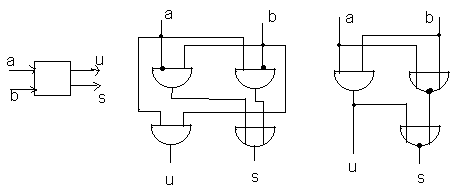Рис. 11. Реализации полусумматора

Не то, что мните вы, природа:

Не слепок, не бездушный лик -

В ней есть душа, в ней есть свобода,

В ней есть любовь, в ней есть язык...

Ф. И. Тютчев