Оцінка дисперсій
Припустимо, що вплив фактора x на вихідний параметр буде відсутній, тобто нуль-гіпотеза про однорідність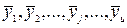 
вірна. Тоді всі серії паралельних спостережень можна розглядати як випадкові вибірки з однієї і тієї ж нормальної сукупності і, адже:
1) не зміщена загальна оцінка дисперсій відновлення s2 по всім u·m спостереженням визначається за виразом
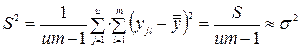(12)
з кількістю ступеней свободи
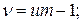
2) вибіркова дисперсія розсіювання «в середині серій», або залишкова оцінка дисперсії відновлення s2 знаходиться як середнє з вибіркових дисперсій по кожній серії окремо
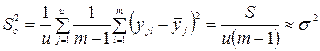(13)
з кількістю ступеней свободи
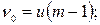
3) вибіркова дисперсія розсіювання між середніми серій є не зміщеною оцінкою дисперсії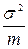 
, з якою нормально розподілені незалежні одна від іншої середні серій:
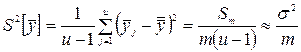(14)
з кількістю ступеней свободи
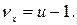
Звідси легко одержуємо третю оцінку дисперсії відновлення, вибіркову дисперсію розсіювання «між серіями»:
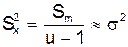(15)
з кількістю ступеней свободи
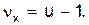
Кількість ступеней свободи перевіряється по співвідношенню
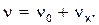
4) В результаті більш глибокого аналізу можна довезти, що S0 і Sx незалежні один від іншого. Зі сказаного очевидно, що через відсутність впливу фактора x вибіркові оцінки S2,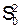 
і Sx однорідні, тому що є оцінками однієї і тієї ж генеральної дисперсії s2.
Припустимо тепер, що вплив фактора x на вихідний параметр істотний, тобто нуль-гіпотеза про однорідність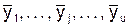 
вірна. Тоді серії паралельних спостережень можна розглядати як випадкові вибірки u незалежних нормально розподілених випадкових величин з однієї і тією же дисперсією (s2 і різними центрами розподілу 
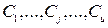і, адже:
1) вибіркова дисперсія s2 характеризує вплив як фактора випадковості, так і фактора x, тобто
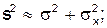(16)
2) оскільки сума S0 не змінюється при заміні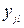 
на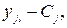 
то вибіркова дисперсія 
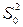також не змінюється і так само є не зміщеною оцінкою для s2, тобто
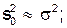(17)
3) оскільки сума Sx враховує не тільки випадкові, але і систематичні розходження між середніми серій і збільшується за рахунок впливу фактора x, то дисперсія 
при цьому також збільшується і перестає бути оцінкою тільки для 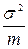, тобто
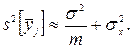
Тому легко одержуємо
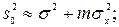(18)
4) незалежність S0 і Sx один від іншого зберігається.
Таким чином, для дисперсії фактора x тепер можна дати дві приблизних оцінки
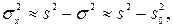(19)
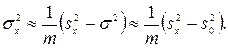(20)
Перша оцінка менш точна через похибки величин S2 і 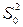. Точність другої вище, тому що дисперсії, які входять в неї, поділені на m.
Виходячи з другого припущення зрозуміло, що при впливі фактора x вибіркові оцінки S2, 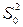, Sx неоднорідні. Отже, зіставляючи ці вибіркові дисперсії, можна прийняти рішення про справедливість першого або другого припущення щодо значимості впливу фактора x (з дисперсією 
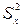) на вихідний параметр. З огляду на точність виразів (19), (20), для оцінки будемо порівнювати дисперсії 
і 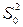.