Геометрическое определение вероятности
Если число исходов некоторого опыта бесконечно, то классическое определение вероятности не может служить характеристикой степени возможности наступления того или иного события. В этом случае пользуются геометрическим подходом к определению вероятности. При этом вероятность события A есть отношение меры A (длины, площади, объема) к мере U пространства элементарных событий.
Геометрическое определение вероятности. Пусть в некоторую область случайным образом бросается точка T, причем все точки области W равноправны в отношении попадания точки T. Тогда за вероятность попадания точки T в область A принимается отношение
,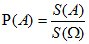
где S(A) и S(W) — геометрические меры (длина, площадь, объем и т.д.) областей A и W соответственно.
1.4Теорема сложения вероятностей формулируется следующим образом.
Вероятность суммы двух несовместимых событий равна сумме вероятностей этих событий:P(A+B)=P(A)+P(B)
Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:
РA (В) = Р (В)
Теорема умножения вероятностей.
Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило:P(AB)=P(A)P(B/A)=P(B)P(A/B)
Доказательство. Докажем теорему для случая, когда опыт имеет конечное число несовместных равновероятных исходов.
Пусть:
·A событие появилось в m исходах опыта;
· B событие появилось в k исходах опыта;
· AB событие появилось в r исходах опыта.
Вероятность события вычислим по классическому определению. Поскольку событие произошло, то всего возможных в этом случае исходов - ; при этом из этих возможных исходов благоприятны событию те исходы, которые составляют событие , т.е. исходов:P(AB)=P(A)P(B/A)
1.5События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.
Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.
Суммой A+B двух событий A и B называют событие, состоящее в появлении события A, или B события , или обоих этих событий.
Суммой нескольких событий называют событие, состоящее в появлении хотя бы одного из этих событий.
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:P(A+B)=P(A)+P(B)
.
Другими словами, вероятность суммы двух несовместных событий равна сумме вероятностей этих.
Следствие. Вероятность появления одного из нескольких попарно несовместных событийA1,A2...An, безразлично какого, равна сумме вероятностей этих событий:P(A1+A2+...+An)=P(A1)+P(A2)+...+P(An)
.
Теорема. Сумма вероятностей попарно несовместных событий , образующих полную группу, равна единице:P(A1)+P(A2)+...+P(An)=1
Следствием правила умножения, и формулы полной вероятности является теорема гипотез или формула Байеса.
По условиям опыта известно, что гипотезы [image] несовместны, образуют полную группу событий:
[image] Ø при [image] и [image].
Вероятности гипотез до опыта (так называемые «априорные вероятности») известны и равны
[image]; [image]
Предположим, что опыт произведен и в результате появилось событие A. Спрашивается, как нужно пересмотреть вероятность гипотез с учетом этого факта, или, другими словами, какова вероятность того, что наступлению события A предшествовала гипотеза [image] (послеопытные вероятности называются апостериорными):
[image].
Вероятность наступления события A совместно с гипотезой Hk определяется с использованием теоремы умножения вероятностей:
P(AÇHk)=P(Hk)×P(A/Hk)=P(A)×P(Hk/A). (3.6)
Таким образом, можно записать:
P (Hk/A) =P (Hk) ×P (A/Hk)/P (A). (3.7)
С использованием формулы полной вероятности
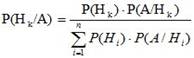 (3.8)
(3.8)
Формула (3.8) называется формулой Байеса. Она позволяет пересчитывать вероятности гипотез в свете новой информации, состоящей в том, что опыт дал результат А