Уравнения функционирования электродвигателя постоянного тока с независимым возбуждением

 

Математическая модель, которая описывает функционирование электродвигателя постоянного тока с независимым возбуждением, может быть получена в виде следующих уравнений.

Уравнение баланса ЭДС:

 

, (30)

 

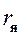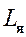где , и 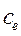– активное сопротивление и индуктивность якорной обмотки и конструктивный параметр электродвигателя, соответственно; , , , – напряжение, ток, поток в магнитном зазоре и скорость вращения якоря электродвигателя, соответственно. Второе слагаемое в правой части (30) 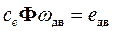принято называть противо-ЭДС, так как это слагаемое имеет размерность ЭДС и вычитается из приложенного к якорю двигателя напряжения .

Отметим, что уравнение (30) фактически является вариантом закона Ома, так как 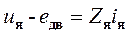, где 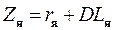– общее (активное и реактивное, т.е. омическое и индуктивное) сопротивление якоря электродвигателя.

 

Уравнение баланса моментов, соответствующее второму закону Ньютона для вращательного движения:

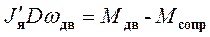, (31)

где – параметр, равный приведенному к валу двигателя моменту инерции всех вращающихся частей. ; 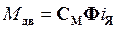– электромагнитный момент, развиваемый двигателем; 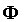– магнитный поток обмотки возбуждения; 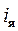– ток в цепи якоря; 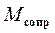– момент всех сопротивлений на валу двигателя, включая приведенные; – конструктивный параметр двигателя.

 

Таким образом, математическая модель электродвигателя в общем случае с учетом принятых обозначений может быть записана в виде системы нелинейных дифференциальных уравнений, если их разрешить относительно производных, т.е. представить в форме Коши:

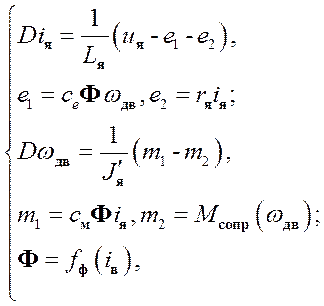(32)

где 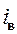– ток в обмотке возбуждения двигателя.

Математическая модель (32) может быть представлена и в виде структурной схемы рис. 7.

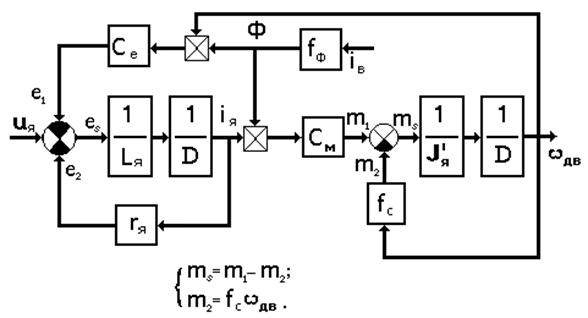Рис. 7. Общая структурная схема двигателя постоянного тока, соответствующая нелинейной математической модели (31). Символ представляет собой операцию умножения переменных.

 

Возможность применения для исследований функционирования исполнительного двигателя и всей простейшей динамической системы управления уравнений (32) ограничена из-за наличия следующих нелинейностей (см. рис. 7):

 

1) двух нелинейностей в виде произведения переменных в слагаемых , ;

2) нелинейной зависимости от относительной скорости момента сил сухого трения (23);

3) нелинейной зависимости магнитного потока от тока возбуждения двигателя .

 

В то же время на первом этапе обычно решаются такие важнейшие вопросы функционирования систем, как их устойчивость (устойчивость системы “в малом”). Для этого следует рассматривать линейное приближение уравнений (32), получаемое в результате операций линеаризации. На рассматриваемом примере покажем некоторые простейшие приемы такой линеаризации.