Простейшие приемы линеаризации математических моделей
В нашем случае имеются две разновидности нелинейностей: гладкие или линеаризуемые относительно некоторой “рабочей точки” и нелинейные характеристики, имеющие разрывы непрерывности первого или второго рода, которые принято считать нелинеаризуемыми. К этому типу нелинейностей может быть отнесена зависимость момента “сухого” трения от относительной скорости вращения. Однако если предположить, что относительная скорость, например, ротора электродвигателя подчиняется гармоническому закону, то такая линеаризация возможна. Для этого вначале определим эквивалентный синусный режим, функционирование в котором равнозначно функционированию в заданном произвольном режиме.
Пусть исходными данными на проектирование простейшей динамической системы управления предусмотрены, как показано в подразделе 3.1, заданная максимальная скорость вращения объекта 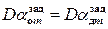 и заданное максимальное ускорение объекта
и заданное максимальное ускорение объекта 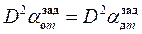 .
.
Введем в рассмотрение эквивалентный синусный режим:
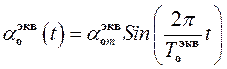 , (33)
, (33)
для которого справедливо равенство амплитуд скорости и ускорения, соответственно:
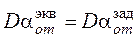 , (34)
, (34)
 . (35)
. (35)
Эквивалентный синусный режим (33) можно считать определенным, если с учетом (34) и (35) найдены амплитуда  и период
и период 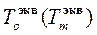 . Для этого достаточно дважды продифференцировать уравнение (33) по времени, что дает следующие выражения:
. Для этого достаточно дважды продифференцировать уравнение (33) по времени, что дает следующие выражения:
 (36)
(36)
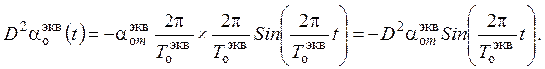 (37)
(37)
Таким образом, с учетом (34) и (35) из (36) и (37) получаем
 , (38)
, (38)
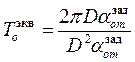 . (39)
. (39)
Очевидно, что при эквивалентном синусном режиме (33) исполнительный двигатель работает также в эквивалентном синусном режиме:
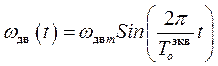 , (40)
, (40)
где 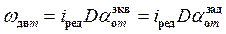 , причем сдвиг фазы на
, причем сдвиг фазы на 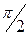 не учитывается, так как начало отсчета времени при определении функции (40) может быть выбрано произвольно.
не учитывается, так как начало отсчета времени при определении функции (40) может быть выбрано произвольно.
Теперь покажем, как для такого эквивалентного синусного режима можно произвести линеаризацию момента “сухого” трения.
Допустим, что рассматриваемая динамическая система управления функционирует при подаче на ее вход гармонического сигнала (33). В этом случае скорость вращения исполнительного двигателя с учетом (40) можно записать в виде гармонической функции. А так как в рассматриваемом случае динамическая система управления работает на неподвижном основании, т.е. 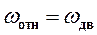 , то зависимость момента трения на валу объекта (23) и соответствующая зависимость от времени момента трения на оси двигателя представит собой нечетную периодическую функцию (рис. 8).
, то зависимость момента трения на валу объекта (23) и соответствующая зависимость от времени момента трения на оси двигателя представит собой нечетную периодическую функцию (рис. 8).
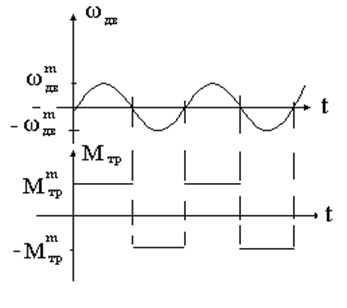
Рис. 8. Линеаризация момента “сухого” трения
Но и в том, и в другом случае такая функция может быть разложена в ряд Фурье:
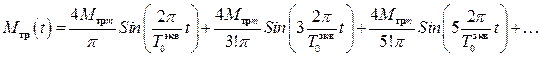 (41)
(41)
Ограничимся только первой гармоникой разложения (41):
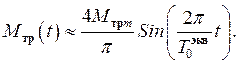 (42)
(42)
Из (40) видно, что
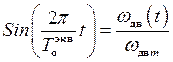 . (43)
. (43)
Следовательно, в первом приближении нелинейная зависимость момента “сухого” трения (23) может быть заменена линейной зависимостью момента эквивалентного “вязкого” трения:
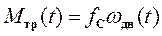 , (44)
, (44)
где 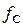 – коэффициент эквивалентного “вязкого” трения, равный:
– коэффициент эквивалентного “вязкого” трения, равный:
 . (45)
. (45)
Проведенная операция представляет собой вариант практического применения известного метода гармонической линеаризации динамических систем управления.