ФОРМУЛИ ТРАПЕЦІЇ.
В формули (1), (2) підставимо 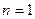 , тоді з формули (2) будемо мати:
, тоді з формули (2) будемо мати:
 ,
,  . Тому
. Тому 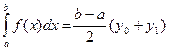 (1)- формула трапецій.
(1)- формула трапецій.
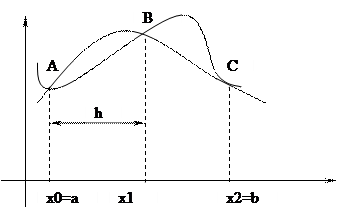
Геометрична інтерпретація:


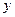




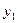


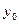
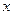
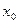
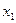
Оцінимо похибку:
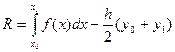
Нехай  - неперервні на
- неперервні на  , запишемо
, запишемо  .
.
Зауважимо, що 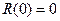 .
.
 ,
,
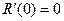 .
.
 .
.
Проінтегруємо послідовно отримані похідні.
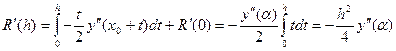 ,
,
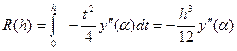 .
.
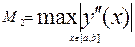 .
.
Тоді 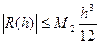 . (2)
. (2)
Поділивши відрізок  на
на 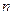 частин точками
частин точками 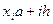 ,
, 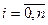 ,
, 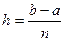 . Застосувавши формулу (1) на кожному з цих відрізків отримаємо :
. Застосувавши формулу (1) на кожному з цих відрізків отримаємо :  (3)- узагальнена формула трапецій.
(3)- узагальнена формула трапецій.
Похибка формули (3) буде рівна сумі похибок на кожному з відрізків.
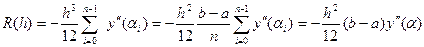 ,
,
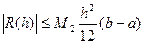
§14
КВАДРАТУРНІ ФОРМУЛИ СІМПСОНА
 У формулу (1) §12 підставимо
У формулу (1) §12 підставимо 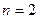 , отримаємо:
, отримаємо: 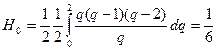 ,
, 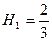 ,
,  . Тоді з формули (1) §12 маємо:
. Тоді з формули (1) §12 маємо:  (1)- квадратурні формули Сімпсона.
(1)- квадратурні формули Сімпсона.
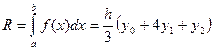 ,
,
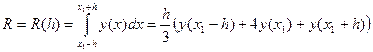 .
.
Обчислимо 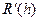 ,
, 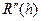 ,
, ,
, 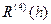 і про інтегрувавши як в попередньому §, отримаємо:
і про інтегрувавши як в попередньому §, отримаємо: 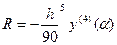 ,
, 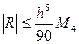 .
.
Розбивши відрізок  на
на  рівних частин точками
рівних частин точками  ,
, 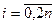 ,
, 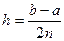 і застосувавши формулу (1) на відповідних парах відрізків отримаємо:
і застосувавши формулу (1) на відповідних парах відрізків отримаємо:
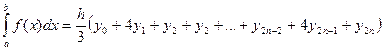 (3)- узагальнена формула Сімпсона.
(3)- узагальнена формула Сімпсона.
Похибка останньої формули буде дорівнювати сумі похибок на відповідних парах відрізків:  ,
, 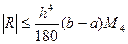 , де
, де 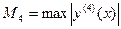 .
.
Для практичної оцінки точності використовують так званий метод подвійного підрахунку.
Нехай похідна змінюється повільно і пропорційно до кроку  в деякому сегменті
в деякому сегменті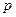 . Обчислимо скориставшись квадратурною формулою інтеграл з кроком
. Обчислимо скориставшись квадратурною формулою інтеграл з кроком  і
і 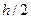 :
:
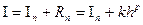 ,
,
 ,
,
віднявши їх одержимо: 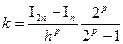
 (4)
(4)
для кожної квадратурної формули значення різне.