НАБЛИЖЕННЯ ЧИСЕЛ. ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ

 

Розділ 1

НАБЛИЖЕННЯ ЧИСЕЛ

 

§1

ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ

 

Означення: задача називається стійкою за вхідними даними, якщо її розв’язок неперервно залежить від вхідних даних. Тобто, якщо малому приросту вхідної величини відповідає малий приріст вихідної. Якщо ця умова не виконується то задача не стійка.

Означення: задача називається коректно поставленою, якщо для будь-яких вхідних даних з деякого класу існує єдиний і стійкий розв’язок.

 

§2

АБСОЛЮТНА І ВІДНОСНА ПОХИБКИ. ПРИЧИНИ ВИНИКНЕННЯ ПОХИБОК

Нехай задане дійсне точне число А. Число а називається наближеним числом до А, якщо воно мало відрізняється від А і може замінити його в… Якщо а<А - наближене з недостачею. Якщо а>А – наближене з надлишком.

ПОХИБКИ АРИФМЕТИЧНИХ ДІЙ

Теорема: гранична абсолютна похибка алгебраїчної суми кількох наближених чисел = сумі граничних абсолютних похибок цих чисел.

Доведення

Доведення

Наслідок: за граничну абсолютну похибку приймають величину:

§4

ЗАГАЛЬНА ПОХИБКА ДЛЯ ФОРМУЛИ

  Нехай задана система величин . Задані похибки . Задана функція. Мета:… . Як правило невеликі, тому другим і вищими їх ступенями можна знехтувати, тоді

НАБЛИЖЕНІ РОЗВ’ЯЗКИ РІВНЯНЬ ТА ЇХ СИСТЕМ

 

§1

ІТЕРАЦІЙНІ МЕТОДИ РОЗВ’ЯЗУВАННЯ РІВНЯНЬ. ПРИНЦИП СТИСКУЮЧИХ ВІДОБРАЖЕНЬ В МЕТРИЧНОМУ ПРОСТОРІ.

Нехай дано рівняння (1). Суть полягає в наступному: нехай в деякій достатньо малій області Д існує єдиний розв’язок рівняння (1). Вибираємо в цій… Означення: метричним простором прийнято називати впорядковану пару , Х -… Означення:Послідовність точок називається фундаментальною, якщо

§2

ВІДОКРЕМЛЕННЯ КОРЕНІВ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ

 

Нехай задано рівняння (1) , де 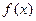визначена і неперервна на деякому скінченному чи нескінченному інтервалі.

Означення: корінь 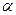рівняння (1) називається відокремленим, якщо існує деякий окіл точки 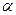в якому не має інших коренів.(для кожного рівняння вказати проміжок, що містить лише один розв’язок)

Задача знаходження наближеного розв’язку рівняння (1) поділяється на два етапи:

1. Відокремлення коренів – виділення якомога вужчих інтервалів в кожному з яких є лише один корінь.
2. Уточнення кореня – зведення його до необмеженого ступеня тосності.

Для відокремлення коренів корисними є твердження:

1. Якщо неперервна функція 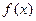на кінцях приймає значення різних знаків, тобто , то на є принаймі один нуль цієї функції. Якщо похідна зберігає знак, то такий нуль єдиний.

2. 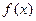є многочлен степеня m, то рівняння (1) не може мати більше ніж m коренів.

Наприклад: Відокремити корені рівняння

 

Визначити кількість коренів зростає на всій числовій осі. Оскільки . , то корінь единий. Запишемо

 

 

 

 

§3

МЕТОД ПОДІЛУ ВІДРІЗКА ПОПОЛАМ

  Нахай задане рівняння . Нехай неперервна на і приймає на кінцях відрізка…

Доведення

За теоремою Лагранжа.

#

 

§4

УТОЧНЕННЯ КОРЕНІВ РІВНЯННЯ МЕТОДОМ ХОРД

Нехай дано рівняння . Залишимо в силі припущення попереднього параграфа. Розглянемо геометричну ітерацію методом хорд.  

Доведення

Підставимо :. Запишемо для f(x) формулу Тейлора і обмежимося 3-ма доданками, тобі:. Підставивши в останню рівність x=c, отримаємо: , оскільки при :…    

Доведення

  Для оцінки точності користуються точністю

§6

МЕТОД ПРОСТОЇ ІТЕРАЦІЇ ДЛЯ РІВНЯННЯ З ОДНІЄЮ ЗМІННОЮ

Якщо послідовність збігається до числа , то перейшовши в (3) отримаємо:є розв’язком (2), а отже (1). Виникають деякі запитання: 1) Які умови повинна задовольняти функція f(x), щоб послідовність (3) була збіжна

Доведення

...

Метод Гауса

Найпростішим методом розв’язування систем лінійних алгебраїчних рівнянь є метод послідовного включення змінних, або метод Гауса. Є кілька… Обмежимося розглядом системи трьох рівнянь з трьома змінними (1)

§8

МЕТОД ПРОСТОЇ ІТЕРАЦІЇ РОЗВ’ЯЗУВАННЯ СИСТЕМИ ЛІНІЙНИХ, АЛГЕБРАЇЧНИХ РІВНЯНЬ

Або (2). Розв’яжемо кожне і-те рівняння відносно змінної . (3), або (4). Виберемо початкове наближення і побудуємо послідовність за формулою (5).

§9

ІТЕРАЦІЙНИЙ МЕТОД ЗЕЙДЕЛЯ

 

Даний метод це модифікований метод простої ітерації.

Нехай задана зведена лінійна система: (1). Виберемо деяке початкове наближення вважаючи, що n – те наближення відоме, будемо шукати (n+1) наближення за таким принципом: .

Як правило метод Зейделя дає кращу збіжність, ніж метод простої ітерації. Бувають випадки коли метод Зейделя збіжний, а метод простої ітерації розбіжний і навпаки.

 

 

§10

ДОСТАТНІ УМОВИ ЗБІЖНОСТІ ІТЕРАЦІЙНИХ ПРОЦЕСІВ

 

Нехай маємо лінійну систему .(1)

Означення: нормою матриці називається додатнє число, яке задовольняє наступні умови:

ü , ,

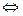
ü , ,

ü ,

ü .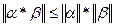

Означення: норму матриці називають канонічною, якщо крім вище перерахованих умов виконуються умови:

ü ,

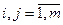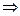
ü , де .

Найчастіше користуються наступними трьома нормами:

,

,

.

Теорема: процес ітерації для системи (1) збігається до єдиного розв’язку, якщо для деякої канонічної норми матриці виконується умова .

Доведення

Виберемо деяке початкове наближення і будуємо послідовність за формулою: ,

, …,.(2) Оскільки , то .

- формула з теорії матричних рядів. Перейшовши до границі в (2) будемо мати: , , - довели, що границя існує, а вона єдина. Теорема доведена.

 

 

§11

ОЦІНКА ПОХИБКИ НАБЛИЖЕНЬ ПРОЦЕСУ ІТЕРАЦІЇ.

Шукають модуль різниці між попереднім і наступним і він має бути меншим за . Нехай задано два послідовні наближення (1) Візьмемо довільне натуральне число р: (2)

§12

МЕТОД КВАДРАТНИХ КОРЕНІВ

 

Нехай задана система рівнянь (1), де - симетрична, тобто для всіх .

Етап: прямий хід.

Всі елементи матриці А відомі, а невідомі елементи. Перемножимо ці матриці:

§13

МЕТОДИ РОЗВ’ЯЗУВАННЯ НЕЛІНІЙНИХ СИСТЕМ

Нехай задана система рівнянь: (1)  

§2

ІНТЕРПОЛЯЦІЙНА ФОРМУЛА ЛАГРАНЖА.

 

На відрізку [a;b] задана система точок і задано значення функції 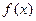в цих точках (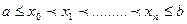, , 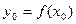,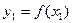…..,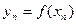). (1)

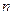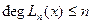Потрібно побудувати поліном степеня не вище , , такий що: ,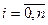.(2)

Спочатку побудуємо поліном , такий що (3). Оскільки на [a;b] згаданий поліном має 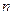нулів, тому цей поліном можна записати у вигляді: .

Підставивши , отримаємо:

. (4)

Знайденні підставимо в (3)

Тоді :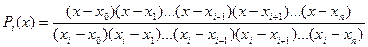. (5)

Будуємо многочлен (6)

або

.(7)

Очевидно, що степінь цього многочлена Лагранжа .

, .

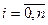Формулу (7) можна записати в компактному вигляді:

,

.

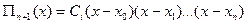Підставивши , отримаємо:

.

Врахувавши останні позначення, отримаємо:

.

 

При 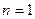многочлен Лагранжа - пряма, яка проходить через точки ,

.

Приклад: для функції побудувати многочлен Лагранжа, взявши вузли інтерполяції , ,.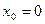

 

 

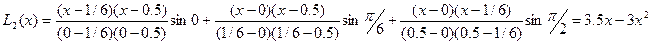
§3

КОЕФІЦІЄНТИ ЛАГРАНЖА. ОЦІНКА ПОХИБКИ ІНТЕРПОЛЯЦІЇ.

Вираз (1) називається коефіцієнтами Лагранжа. Тоді многочлен Лагранжа набере вигляду: (2). Зауважимо, що форма коефіцієнтів Лагранжа інваріантна… У випадку рівновіддалених вузлів інтерполяції вираз для коефіцієнтів Лагранжа… Нехай , , ,…,,- деякий крок.

§4

CКІНЧЕННІ РІЗНИЦІ

Нехай задана функція . Позначимо - скінченну величину приросту аргументу. Означення: вираз (1) називається першою скінченною різницею функції . Означення: скінченною різницею порядку функції називають величину ,

Доведення

Якщо функція задана табличними значеннями , точки - рівновіддалені, , то скінченні різниці зручно записувати у вигляді таблиць. Розглянемо це на прикладі: скласти горизонтальну таблицю різниць функції ,… 7. . Скінчена різниця виражена через послідовність значень функції.

§6

ПЕРША ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА.

 

Нехай задана таблиця значень функції 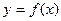, тобто дано, що , , 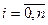. Поставимо завдання знайти поліном : і для всіх 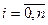. Остання умова еквівалентна тому, що .

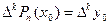Многочлен будемо шукати у вигляді: (1)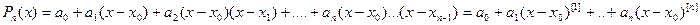В дану рівність підставимо 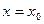: .(2)

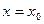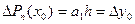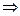
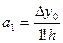Обчислимо першу скінчену різницю: , в дану рівність підставимо : (3) . , підставивши 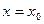, отримаємо: ,

.(4)

В загальному випадку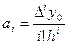.(5)

Формули (2), (3), (4), (5) підставимо в (1), отримаємо:

(6)- перший інтерполяційний поліном Ньютона.

,

.

Для використання на практиці формулу (6) спрощують. Покладемо: 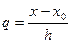- кількість кроків, яка необхідна для того, щоб від точки 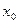перейти до точки .

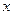Тоді . З (6) будемо мати: .

Зауваження: якщо задана необмежена таблиця значень функції, то число 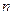вибирають так, щоб різниця була сталою з заданою точністю. Першу інтерполяційну формулу Ньютона зручно використовувати для інтерполяції та екстраполяції функції, коли .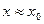

Для оцінки похибки користуються формулою: , де

Наприклад: знайти інтерполяційний поліном Ньютона для функції на відрізку , взявши .

 

x	y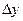
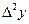
3.5	33.115	1.698	0.087	0.005
3.55	34.813	1.785	0.092	0.003
3.6	36.598	1.877	0.095
3.65	38.475	1.972
3.7	40.441

Бачимо, що треті різниці дуже мало відрізняються, беремо .

 

§7

ДРУГА ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА.

 

При всіх умовах попереднього параграфа многочлен будемо шукати у вигляді: .(1)

Поклавши в (1) , будемо мати: 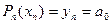.(2) Взявши різницю і поклавши : 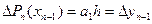, .(3) Взявши другу різницю і підставивши , отримаємо: , (4) і т. д.

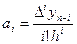
Підставимо знайдені коефіцієнти в рівність (1):

- друга інтерполяційна формула Ньютона.

Позначимо: ,

,

.

Тому .

Зауваження: другу інтерполяційну формулу Ньютона зручно використовувати для інтерполяції та екстраполяції функції у випадку, коли 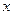близьке до .

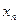Для оцінки похибки використовують формулу: .

Наприклад: маючи таблицю значень функції в межах від до з кроком знайти значення , .

 

 

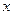
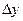
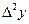
	0.2588	0.0832	-0.0026	-0.0006
	0.3420	0.0800. 0.0806	-0.0032	-0.0006
	0.4226	0.0774	-0.0038	-0.0006
	0.5	0.0736	-0.0044	-0.0006
	0.5736	0.0692	-0.0049	-0.0006
	0.6428	0.0643	-0.0054	-0.0005
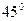
	0.7071	0.0589	-0.0057
	0.7660	0.0532
	0.8192

.

 

.

 

 

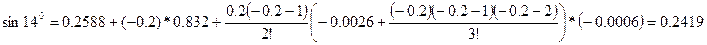§8

ПОСТАНОВКА ЗАДАЧІ ЧИСЕЛЬНОГО ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЇ.

 

Якщо функція f(x) задана таблично або складним аналітичним виразом, то для знаходження її похідних використовують чисельне диференціювання. Для цього на , який поділений на частини точками 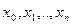будують інтерполяційну функцію 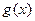, а далі вважають, що , …, при цьому похибка , .

Якщо в околі деякої точки 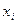виконується, то це не означає, що.

Операція наближеного диференціювання менш точна ніж інтерпуляція.

 

Менше наближення чим більш співпадають дотичні. Невелика різниця між значеннями f(x) і g(x) в точці , зовсім не гарантує такоїж невеликої різниці між значеннями похідних цих функцій.

 

§9

ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ ІНТЕРПОЛЬОВАНИХ

МНОГОЧЛЕНАМИ НЬЮТОНА.

Врахувавши, що похідна:

§10

ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ ІНТЕРПОЛЬОВАНИХ МНОГОЧЛЕНАМИ ЛАГРАНЖА.

 

Залишимо в силі умови попереднього параграфа. Замінимо функцію 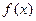інтерполяційним многочленом:

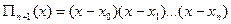, поділимо кожну дужку на і домножимо на .

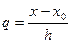
тоді ,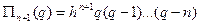

,

підставимо .

Тоді 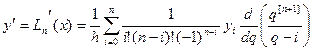. Похибка у випадку многочлена Лагранжа рівна: ,

.

У випадку, коли , тоді .

Зауваження: часто похибка, яка виникає при обчисленні похідних може набагато перевищувати похибку задання самої функції(навіть може зростати до ).

Наприклад:

 

§11

ЗАДАЧА ЧИСЕЛЬНОГО ІНТЕГРУВАННЯ ФУНКЦІЇ. ФОРМУЛИ ПРЯМОКУТНИКІВ.

Однією з найпростіших квадратурних формул є формула прямокутників.                         …

§12

КВАДРАТУРНІ ФОРМУЛИ НЬЮТОНА-КОТЕСА.

, . (1)- формула Ньютона-Котеса (2)- коефіцієнти Котеса.

§13

ФОРМУЛИ ТРАПЕЦІЇ.

, . Тому (1)- формула трапецій. Геометрична інтерпретація:  

§15

КУСКОВО-КУБІЧНА СПЛАЙН ІНТЕРПОЛЯЦІЯ.

Найчастіше використовують випадок . Нехай на задана неперервна функція , задане розбиття відрізка точками: , для всіх . Кубічним сплайном, який наближає дану функцію будемо називати функцію , яка… а) на кожному з відрізків ;

§16

ДЕЯКІ ВІДОМОСТІ ПРО РІЗНИЦЕВІ РІВНЯННЯ.

Означення: Різницевим рівнянням називається рівняння відносно функції дискретної змінної.

(1) Відмітимо, що це рівняння називається лінійним різницевим рівнянням к-того… Означення: Рівняння (2) називається лінійним однорідним різницевим рівнянням.

§17

МНОГОЧЛЕНИ ЧЕБИШЕВА.

 

- позначаються, . Задаються наступними рівностями: , , 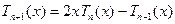. (1) Використовуючи рекурентні формули (1), отримаємо: , .

Відмітимо, що коефіцієнт біля в многочлена дорівнює , всі многочлени з індексами - парні, з індексами - непарні.

Відомо, що ,

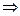
Позначимо .

Отримаємо: .(2)

Порівнюючи (1) і (2) бачимо, що функція 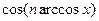задовольняє рекурентне співвідношення (1). Початкові умови: , . Таким чином:

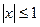(3). З даної рівності випливає, що при . (4)

Зауваження: нерівність (4) не буде справедливою при всіх 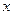. Якщо , то , а 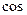такого числа не завжди менше 1.

Рекурентне співвідношення (1) є різницевим рівнянням. Позначимо , тоді отримаємо характеристичне рівняння:

Якщо 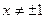, то корені прості, а тому . Замість 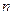підставимо 1, отримаємо: або .

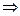
Тому . (5) – многочлен Чебишева

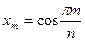Зауваження: з нерівностей (4) випливає, що многочлени Чебишева набувають значення тоді, коли , , , , де .

Означення:Многочлен називають многочленом, який найменше відхиляється від нуля. Таке означення пояснюється наступною теоремою:

Теорема: Якщо з старшим коефіцієнтом рівним одиниці, то .

Теорема доводиться методом від супротивного .

Заміною змінної проміжок переводимо взаємно однозначно в проміжок . Тоді многочлен з старшим коефіцієнтом називається многочленом Чебишева на . Аналогічно як ми робили для , можна побудувати многочлен, який найменше відхиляється на .

Цей многочлен запишеться: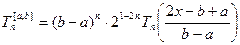

Розглянемо значення многочленна

Отримали, що многочлен степеня n-1 має n нулів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.

 

§18

НАБЛИЖЕННЯ ФУНКЦІЙ В ЛІНІЙНОМУ НОРМОВАНОМУ ПРОСТОРІ. УМОВИ ІСНУВАННЯ ТА ЄДНОСТІ ЕЛЕМЕНТА НАЙКРАЩОГО НАБЛИЖЕННЯ.

Означення:довільний елемент для якого виконується умова (*) називається елементом найкращого наближення для функції Теорема 1:Для в множині існує елемент найкращого наближення, множина таких… Зауваження: елемент найкращого наближення не обов’язково один. Наприклад, розглянемо простір векторів з нормою .…

§19

СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ ФУНКЦІЙ.

N.1 НАБЛИЖЕННЯ АЛГЕБРАЇЧНИМИ МНОГОЧЛЕНАМИ.

Для довільних функцій скалярний добуток задамо так: . Легко перевірити, що всі аксіоми скалярного добутку тут виконуються, якщо дві функції, які… Означення: Найкраще наближення в просторі називається найкращим… В якості лінійно-незалежної системи візьмемо функції: , елемент найкращого наближення будемо шукати в множині…

N. 2 ДИСКРЕТНЕ СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ.

Многочлен найкращого наближення шукаємо у вигляді: . Відповідно до загальної теорії для знаходження цього многочлена потрібно… З врахуванням ортогональності

N.3 СЕРЕДНЬОКВАДРАТИЧНЕ НАБЛИЖЕННЯ ТРИГОНОМЕТРИЧНИМИ МНОГОЧЛЕНАМИ.

  §21 НАЙКРАЩЕ РІВНОМІРНЕ НАБЛИЖЕННЯ. ТЕОРЕМА ЧЕБИШЕВА

Доведення

де підберемо так щоб

§21

ТЕОРЕМА ВЕЄРШТРАСА

 

Лема1: Справедлива рівність:

Доведення

Оскільки 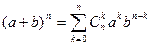а=х, b=(1-х)

 

Лема2: Справедлива рівність:

 

Доведення Леми

Маємо суму

Згідно Леми1:

Тоді: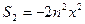

Далі:

Тоді

 

Теорема: Нехай f(x) неперервна на [a,b], тоді для ">0, існує :

 

Доведення Теореми

Розглянемо многочлен Бернштейна: (1) Покажемо, що при великих n він задовольняє умови теореми.

Тригонометричні многочлени найкращого наближення.

Теорема: (ІІ Теорема Веєрштраса): Якщо f(x) неперервна, періодична з періодом…

Побудова алгебраїчних многочленів

Найкращого наближення.

Ефективних способів точної побудови многочлена найкращого наближення до даної функції не існує. Тому розглянемо чисельні методи розв‘язку цієї… Зробимо деякі розрахунки які покажуть нам алгоритм побудови многочлена…  

Розділ 4

Метод Ейлера.

Вибираємо досить малий крок h, і будуємо систему рівновіддалених точок: , Інтервальну криву яка є розв‘язком рівняння (1) і проходить через точку , замінюємо ламаною . З вершинами ланки якої в…

Модифікації методу Ейлера.

Дано , (1) Задано систему точок 1) Знаходимо т і

Методи Рунге-Кутта.

Задано диференціальне рівняння: (1) і початкова умова: . Позначимо: Вважатимемо, що має неперервні частинні похідні до деякого порядку , тоді розв‘язок має похідні порядку.

Метод Адамса

(1) Задана система точок:

Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами.

(1) і крайові умови: (2) або (2‘)

Метод прогонки розв’язування крайових задач для звичайних диференціальних рівнянь другого порядку.

Нехай задане диференціальне рівняння: (1) (2)