Означення: Різницевим рівнянням називається рівняння відносно функції дискретної змінної.
Розглянемо найпростіший випадок одного лінійного рівняння відносно невідомої функції одного цілочисельного аргументу.
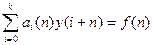 (1)
(1)
Відмітимо, що це рівняння називається лінійним різницевим рівнянням к-того порядку. Воно є дискретним аналогом лінійного диференціального рівняння порядку k рівняння: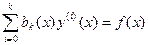 .
.
Означення: Рівняння  (2) називається лінійним однорідним різницевим рівнянням.
(2) називається лінійним однорідним різницевим рівнянням.
Теорема: Якщо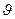 є деякий частинний розв’язок рівняння (1), то
є деякий частинний розв’язок рівняння (1), то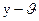 є розв’язком однорідного рівняння (2).
є розв’язком однорідного рівняння (2).
Означення:Система 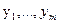 розв’язок рівняння (2) називається лінійно незалежною, якщо з того, що
розв’язок рівняння (2) називається лінійно незалежною, якщо з того, що 
Теорема: Якщо деякі функції  є розв’язком однорідного рівняння (2), то лінійна комбінація
є розв’язком однорідного рівняння (2), то лінійна комбінація 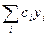 теж є розв’язком рівняння (2)
теж є розв’язком рівняння (2)
Мають місце наступні твердження:
1. Загальний розв’язок неоднорідного рівняння дорівнює сумі його частинного розв’язку і загального розв’язку відповідного однорідного рівняння.
2. Якщо функції  є розв’язками однорідного рівняння (2), то
є розв’язками однорідного рівняння (2), то 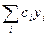 теж є розв’ язком рівняння (2).
теж є розв’ язком рівняння (2).
3. Якщо 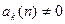 , то загальний розв’ язок рівняння (2) можна записати у вигляді:
, то загальний розв’ язок рівняння (2) можна записати у вигляді: 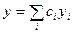 , де
, де  - лінійно-незалежні розв’ язки рівняння (2).
- лінійно-незалежні розв’ язки рівняння (2).
Означення: Якщо в рівняннях (1) і (2) коефіцієнти 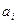 не залежать від
не залежать від 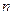 , то такі рівняння називаються рівняннями з сталими коефіцієнтами.
, то такі рівняння називаються рівняннями з сталими коефіцієнтами.
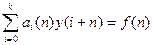 (
(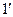 )
)
 (
( )
)
розв’ язок рівняння (2) будемо шукати у вигляді: 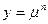 . Тобто
. Тобто 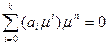 .
.
Бачимо, що кожному кореню рівняння 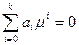 відповідає частинний розв’ язок рівняння (
відповідає частинний розв’ язок рівняння ( ), а саме
), а саме 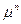 . Якщо всі корені характеристичного рівняння прості, то маємо к-різних розв’язків. Якщо деякий корінь має кратність
. Якщо всі корені характеристичного рівняння прості, то маємо к-різних розв’язків. Якщо деякий корінь має кратність 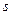 , то йому відповідають розв’язки:
, то йому відповідають розв’язки: 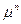 ,
, 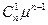 , …,
, …,
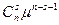 .
.