НАБЛИЖЕННЯ ФУНКЦІЙ В ЛІНІЙНОМУ НОРМОВАНОМУ ПРОСТОРІ. УМОВИ ІСНУВАННЯ ТА ЄДНОСТІ ЕЛЕМЕНТА НАЙКРАЩОГО НАБЛИЖЕННЯ.
Нехай 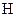 - лінійний нормований простір,
- лінійний нормований простір, 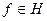 ,
, 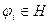 -лінійно-незалежні елементи. Через
-лінійно-незалежні елементи. Через 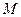 позначимо лінійний підпростір узагальнених многочленів виду
позначимо лінійний підпростір узагальнених многочленів виду 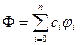 , де
, де  . Множина
. Множина 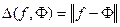 , де
, де  , обмежена знизу наприклад нулем. Тому існує
, обмежена знизу наприклад нулем. Тому існує 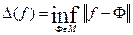 - найкраще наближення. Виникає питання чи в множині
- найкраще наближення. Виникає питання чи в множині 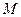 існує елемент
існує елемент  :
: 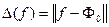 (*). Якщо такий елемент існує, то його називають елементом найкращого наближення функції
(*). Якщо такий елемент існує, то його називають елементом найкращого наближення функції 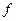 многочленами з множини
многочленами з множини 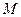 .
.
Означення:довільний елемент 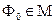 для якого виконується умова (*) називається елементом найкращого наближення для функції
для якого виконується умова (*) називається елементом найкращого наближення для функції 
Теорема 1:Для 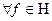 в множині
в множині 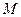 існує елемент найкращого наближення, множина таких елементів опукла.
існує елемент найкращого наближення, множина таких елементів опукла.
Зауваження: елемент найкращого наближення не обов’язково один. Наприклад, розглянемо простір 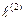 векторів
векторів 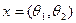 з нормою
з нормою  . Візьмемо точку
. Візьмемо точку 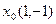 і візьмемо одновимірний підпростір
і візьмемо одновимірний підпростір  з базисними векторами
з базисними векторами 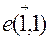 . Очевидно, що
. Очевидно, що  при
при 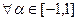 . Таким чином маєм нескінченну множину елементів найкращого наближення.
. Таким чином маєм нескінченну множину елементів найкращого наближення.
Теорема 2: Якщо простір 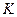 строго – нормований, то елемент найкращого наближення єдиний.
строго – нормований, то елемент найкращого наближення єдиний.
Теорема 3: (характеристика елемента найкращого наближення) Якщо в множині 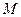 існує елемент
існує елемент 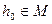 - елемент найкращого наближення для функції
- елемент найкращого наближення для функції 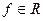 , то тоді для
, то тоді для 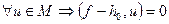 .
.
Теорема 4: Якщо 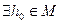 :
: 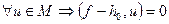 , то
, то  - елемент найкращого наближення для функції f многочленна М.
- елемент найкращого наближення для функції f многочленна М.
Як побудувати елемент найкращого наближення в просторі з скалярним добутком?
Нехай 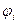 ,
, 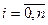 - лінійно-незалежні елементи. Комбінації
- лінійно-незалежні елементи. Комбінації 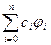 утворюють лінійний простір. Якщо деякий елемент
утворюють лінійний простір. Якщо деякий елемент 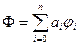 є елементом найкращого наближення для функції
є елементом найкращого наближення для функції 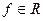 , то згідно з теоремою 3 різниця
, то згідно з теоремою 3 різниця  ортогональна до всіх елементів підпростору
ортогональна до всіх елементів підпростору 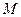 , в тому числі й до елементів
, в тому числі й до елементів 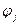 ,
, 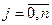 . Тобто
. Тобто 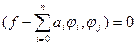 (1) для
(1) для  . Оскільки елемент найкращого наближення існує, то система (1) має розв’язок. Користуючись теоремою 4 можна довести, що
. Оскільки елемент найкращого наближення існує, то система (1) має розв’язок. Користуючись теоремою 4 можна довести, що 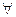 розв’язок системи (1) є елементом найкращого наближення функції
розв’язок системи (1) є елементом найкращого наближення функції 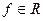 . Методом від супротивного можна довести, що такий елемент єдиний. Таким чином в просторі з скалярним добутком відшукання елемента найкращого наближення виду
. Методом від супротивного можна довести, що такий елемент єдиний. Таким чином в просторі з скалярним добутком відшукання елемента найкращого наближення виду 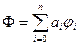 зводиться до розв’язання системи лінійних алгебраїчних рівнянь (1), яку зручніше записати у вигляді:
зводиться до розв’язання системи лінійних алгебраїчних рівнянь (1), яку зручніше записати у вигляді:  ,
, 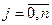 . (2)
. (2)