Решение игр 2хn, mх2.
Рассмотрим сначала игру 2´n с платежной матрицей
.
Будем предполагать, что седловой точки матрица A не имеет. Произвольную смешанную стратегию игрока 1 представим в виде 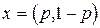 , где
, где 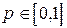 . Если игрок 1 применяет смешанную стратегию x, а игрок 2 — свою j–ю чистую стратегию, то выигрыш игрока 1, очевидно, равен , то есть линейно зависит от p.
. Если игрок 1 применяет смешанную стратегию x, а игрок 2 — свою j–ю чистую стратегию, то выигрыш игрока 1, очевидно, равен , то есть линейно зависит от p.
По теореме
.
Исходя из этого соотношения, с помощью простых геометрических построений легко найти решение игры:
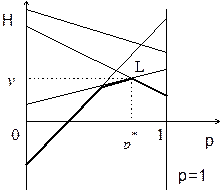 Рис. 1.
Рис. 1.
|
- строим графики функций 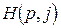 для
для 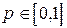 . Получим n прямых (см. рис. 1). Эти прямые удобно строить по двум точкам —
. Получим n прямых (см. рис. 1). Эти прямые удобно строить по двум точкам —  и
и 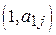 . Первая из них находится на оси ординат H, вторая — на оси
. Первая из них находится на оси ординат H, вторая — на оси  ;
;
- строим график функции
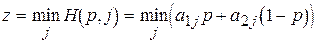 —
—
нижнюю огибающую всех прямых, соответствующих стратегиям игрока 2. Значения этой функции, соответствуют выигрышу игрока 1, когда он применяет стратегию 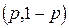 , а противник действует наихудшим для него образом. На рис. 1 нижняя огибающая выделена жирной линией;
, а противник действует наихудшим для него образом. На рис. 1 нижняя огибающая выделена жирной линией;
- наивысшая точка нижней огибающей (точка L на рис. 1) соответствует тому значению p, при котором достигается
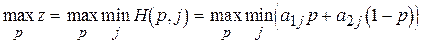 .
.
Поэтому ордината точки L является значением игры, а ее абсцисса — первой компонентой оптимальной смешанной стратегии игрока 1: 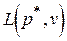 .Если же таких высших точек будет более одной, т.е. огибающая будет иметь наивысший огибающий участок, то у игрока 1 существует бесконечное множество оптимальных смешанных стратегий, первые компоненты которых соответствуют абсциссам точек этого горизонтального участка.
.Если же таких высших точек будет более одной, т.е. огибающая будет иметь наивысший огибающий участок, то у игрока 1 существует бесконечное множество оптимальных смешанных стратегий, первые компоненты которых соответствуют абсциссам точек этого горизонтального участка.
Описанное построение позволяет исходную игру 2´n свести к игре 2´2. Так как матрица игры не имеет седловой точки, то 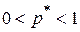 и в точке L пересекается не менее двух прямых с противоположным наклоном. Пусть
и в точке L пересекается не менее двух прямых с противоположным наклоном. Пусть 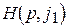 и
и 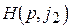 такие прямые. Интуитивно ясно, что игрок 2, пользуясь только двумя стратегиями
такие прямые. Интуитивно ясно, что игрок 2, пользуясь только двумя стратегиями 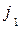 и
и 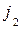 , может не дать игроку 1 выиграть больше, чем v. Таким образом, оптимальное поведение в игре 2´2:
, может не дать игроку 1 выиграть больше, чем v. Таким образом, оптимальное поведение в игре 2´2:
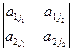
является оптимальным и в исходной игре 2´n. Решение игры легко получить по формулам для игр 2х2.
В случае, когда нижняя огибающая имеет верхний горизонтальный участок, соответствующий чистой стратегии 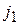 , то
, то 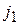 будет единственной чистой оптимальной стратегией игрока 2.
будет единственной чистой оптимальной стратегией игрока 2.
Пусть теперь две чистые стратегии имеет игрок 2, а игрок 1 — произвольное их число. Матрица такой игры имеет вид:
| Рис. 2. |
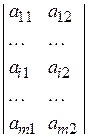 .
.
 Анализ этой игры выполняется аналогично предыдущему случаю. Отличие состоит лишь в том, что теперь, чтобы учесть интересы игрока 2, нужно исходить из соотношения (теорема):
Анализ этой игры выполняется аналогично предыдущему случаю. Отличие состоит лишь в том, что теперь, чтобы учесть интересы игрока 2, нужно исходить из соотношения (теорема):
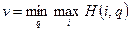 ,
,
где q — первая компонента смешанной стратегии игрока 2, а 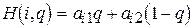 .
.
Для перехода от исходной игры 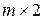 к игре
к игре 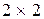 используется точка
используется точка 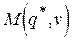 — нижняя точка верхней огибающей семейства прямых
— нижняя точка верхней огибающей семейства прямых 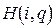 (рис. 2).
(рис. 2).
Пример. Рассматривается задача разработки оптимального плана энергетического строительства в некотором регионе. Предположим, что имеются возможности строительства электростанций четырех типов: 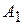 ,
, 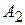 ,
, 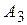 и
и 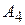 (тепловые, гидравлические и т.д.). Эффективность каждого из четырех типов объектов зависит от разнородных факторов (наводнения, засуха, морозы), а также от цены топлива, расходов на его транспортирование и т. п. Допустим, что можно выделить (по крайней мере, ориентировочно) пять различных случаев, каждый из которых обозначает определенное сочетание факторов, влияющих на возможную эффективность энергетических объектов. Назовем их состояниями природы и обозначим через
(тепловые, гидравлические и т.д.). Эффективность каждого из четырех типов объектов зависит от разнородных факторов (наводнения, засуха, морозы), а также от цены топлива, расходов на его транспортирование и т. п. Допустим, что можно выделить (по крайней мере, ориентировочно) пять различных случаев, каждый из которых обозначает определенное сочетание факторов, влияющих на возможную эффективность энергетических объектов. Назовем их состояниями природы и обозначим через 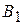 ,
,  ,
, 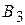 ,
,  и
и 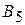 .
.
Экономическая эффективность отдельных типов электростанций изменяется в зависимости от состояния природы в соответствии со следующей таблицей:
| Состояния природы | ||||||
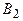
| 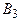
| 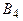
| 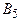
| |||
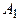
| ||||||
| Типы | 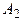
| |||||
| электростанций | 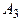
| |||||
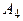
|
Будем рассматривать описанную ситуацию как игровую. Первый игрок (планирующие органы) располагает четырьмя стратегиями (по числу типов электростанций). Второй игрок («природа») действует случайно, но так, что к явлениям природы невозможно применить положения теории вероятностей. У него пять стратегий. В этих условиях табл. является, по существу, игровой матрицей. Ее анализ показывает, что у игрока 1 стратегии 1 и 2 доминируются стратегией 3 и поэтому могут быть исключены из рассмотрения. Приходим к игре с матрицей:
Теперь замечаем, что у игрока 2 стратегия 3 доминируется стратегией 2, а стратегия 2 — стратегией 4. Следовательно, имеет смысл анализировать игру 2´3, задаваемую матрицей:
Пусть 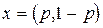 — произвольная смешанная стратегия игрока 1 в этой игре. Найдем функции
— произвольная смешанная стратегия игрока 1 в этой игре. Найдем функции 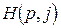 ,
, 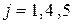 :
:
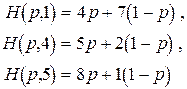
и построим их графики (рис. 3)
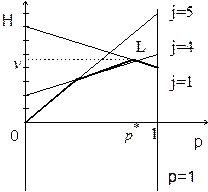 Рис. 3.
Рис. 3.
|
Экстремальная точка L на нижней огибающей (отмечена жирной линией) является пересечением прямых, соответствующих 1–ой и 4–ой стратегиям игрока 2, поэтому рассматриваем игру 2´2:
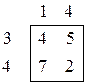
По формулам находим:
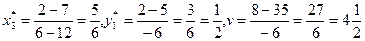 Из полученных результатов формируем решение исходной игры:
Из полученных результатов формируем решение исходной игры:
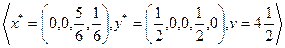 .
.
Таким образом, для обеспечения региона электроэнергией целесообразно ограничиться строительством электростанций типов 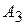 и
и 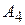 в пропорции
в пропорции 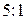 . При этом экономическая эффективность такого решения никогда не будет ниже 4.5; если же учесть, что второй игрок — природа — скорее всего не будет применять своей оптимальной стратегии, то можно рассчитывать на более высокий показатель эффективности.
. При этом экономическая эффективность такого решения никогда не будет ниже 4.5; если же учесть, что второй игрок — природа — скорее всего не будет применять своей оптимальной стратегии, то можно рассчитывать на более высокий показатель эффективности.