Теорема про складання швидкостей
Згідно з рис. 107 в кожному положенні точки має місце векторна рівність
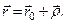 (г)
(г)
Оскільки 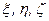 –координати точок
–координати точок  в рухомій системи координат, а
в рухомій системи координат, а 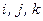 – її орти, то
– її орти, то
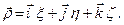 (д)
(д)
Підставляючи (д) в (г), отримаємо
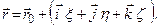
Отриману векторну рівність продиференціюємо за часом. Враховуючи, що 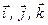 є змінними векторами, отримаємо
є змінними векторами, отримаємо
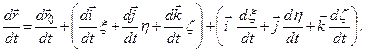 (e)
(e)
Вираз  , враховуючи (д), є не що інше, як похідна за часом від радіуса-вектора
, враховуючи (д), є не що інше, як похідна за часом від радіуса-вектора 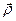 за умови, що
за умови, що  , тобто
, тобто

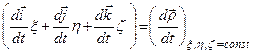 .
.
Аналогічно вираз  є похідною від
є похідною від 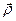 за часом при умові, що
за часом при умові, що 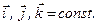
Враховуючи сказане, маємо
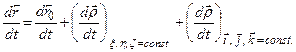 . (є)
. (є)
Оскільки
1)  – це абсолютна швидкість точки
– це абсолютна швидкість точки  (див. формулу (а));
(див. формулу (а));
2) 
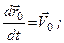
3)  , адже координати точки
, адже координати точки 
 є одночасно і координатами точки
є одночасно і координатами точки  (див. рис. 107), а для точки
(див. рис. 107), а для точки  вони є постійними;
вони є постійними;
4)  – відносна швидкість точки
– відносна швидкість точки  (див. формулу (б)), то рівність (є) набуває вигляду
(див. формулу (б)), то рівність (є) набуває вигляду
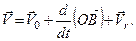
За формулою (2.31)

Швидкість точки  для точки, що здійснює складний рух, є переносною швидкістю
для точки, що здійснює складний рух, є переносною швидкістю 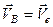 (див. формулу (в)). Остаточно маємо
(див. формулу (в)). Остаточно маємо
 . (2.58)
. (2.58)
Формула (2.58) виражає теорему про складання швидкостей, яка читається так: