рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Предмет теоретичної механіки Теоретична механіка – це одна з дисциплін науки Механіка
Реферат Курсовая Конспект
Предмет теоретичної механіки Теоретична механіка – це одна з дисциплін науки Механіка
Предмет теоретичної механіки Теоретична механіка – це одна з дисциплін науки Механіка - раздел Философия, Предмет Теоретичної Механіки ...
Предмет теоретичної механіки
Теоретична механіка – це одна з дисциплін науки “Механіка”. Саме слово “механіка” грецького походження і в прямому перекладі означає “хитрість”. Цей термін вперше був застосований у ІІІ ст. до н.е. одним з учнів Арістотеля при вив-ченні таких явищ, в яких “менше зусилля перемагає більше”, наприклад, при підніманні вантажу за допомогою важеля.
Механіка – це наука про найпростішу форму руху матерії – механічний рух.
Механічним рухом називається переміщення одного матеріального об’єкта (або його частини) відносно іншого (іншої його частини) в просторі й часі.
Так, наприклад, під час руху автомобіля по дорозі одне тіло (автомобіль) переміщується відносно інших тіл (дерев, будинків), які знаходяться при дорозі. При розтягуванні або стискуванні пружини одна її частина переміщується відносно іншої. Такий рух називається деформацією, вивченням якої займаються такі дисципліни механіки, як опір матеріалів і
теорія пружності.
Теоретична механіка вивчає найбільш загальні закони механічного руху, який визначається переміщенням одного матеріального об’єкта відносно іншого.
Основним завданням теоретичної механіки є пізнання кількісних і якісних закономірностей механічного руху та відображення їх на математичній мові у… Закони, сформульовані теоретичною механікою, є об’єк-тивними. Їх об’єктивність… “Пришвидшення, з яким рухається матеріальна точка, пропорційне діючій силі і обернено пропорційне її масі”.Основні поняття теоретичної механіки
Розглянемо тільки ті поняття, без яких неможливо приступити до вивчення теоретичної механіки і які є загальними для трьох її частин. До таких понять належать поняття матеріальної точки, механічної системи і твердого тіла.
Матеріальна точка – це тіло, розмірами якого в даних умовах (при розв’язанні даної задачі) можна знехтувати.
Поняття матеріальної точки є відносним. Відносність його, по-перше, полягає в тому, що одне і те ж саме тіло при розв’язанні однієї задачі приймають за матеріальну точку, а при розв’язанні іншої – ні. По-друге, при розв’язанні одних задач (наприклад, при дослідженні руху планет навколо Сонця) величезні тіла (планети) приймають за матеріальну точку, а при розв’язанні інших – навіть мікротіла не можна брати за матеріальну точку.
Механічна система – це сукупність матеріальних точок (тіл), положення і рухи яких взаємопов’язані між собою.
Згідно з цим визначенням до механічної системи належать фізичні тіла, механізми і т.д. Однак купа піску (гравію), гурт людей не належать до механічної системи, бо положення і рух окремих частин такої системи переважно не взаємопо-в’язані.
Особливе місце в теоретичній механіці посідає незмінна система.
Незмінною називається механічна система, під час руху якої її елементи, що контактують безпосередньо між собою, зберігають взаємне розміщення один відносно одного.
Частковим, найпростішим, прикладом незмінної системи є абсолютно тверде тіло.
Абсолютно твердим тілом (твердим тілом) називається незмінна механічна система, для якої відстань між будь-якими двома точками залишається незмінною під час її руху.
Поняття про абсолютно тверде тіло є абстракцією. Всі тіла в природі деформуються. Однак в багатьох випадках зміна форми тіла є незначною і при дослідженні руху тіла нею можна знехтувати і розглядати його як абсолютно тверде. В подальшому абсолютно тверде тіло будемо називати просто твердим тілом.
Матеріальна точка, тверде тіло, механічна система є основними матеріальними об’єктами, закони руху яких вивчаються в теоретичній механіці. Кожен з цих об’єктів може перебувати в певному кінематичному стані – у стані спокою або здійснювати деякий рух.
СТАТИКА ТВЕРДОГО ТІЛА
Предмет статики твердого тіла
Статика твердого тіла (статика) – це розділ теоретичної механіки, в якому розглядається перетворення системи сил в еквівалентні їм системи і визначаються умови рівноваги твердих тіл під дією різних систем сил.
Основними завданнями статики є:
1. Перетворення системи сил, що діють на тверде тіло, в системи, їм еквівалентні.
2. Визначення умов рівноваги системи сил, що діють на тверде тіло.
3. Визначення положення центра ваги твердого тіла, системи тіл.
Найголовнішим з цих завдань є визначення умов, яким повинна задовольняти система сил, що діє на тверде тіло, щоб воно знаходилось в рівновазі.
Основні поняття статики
1. Сила – це фізична величина, яка є мірою взаємодії матеріальних об’єктів і вказує на інтенсивність і напрям даної взаємодії. Таке визначення сили не є всеохоплюючим. Не кожну взаємодію (наприклад,… З визначення випливає, що сила – це вектор. Як кожний вектор, сила характеризується точкою прикладання, напрямом і…В’язі та їх реакції
Всі тіла в природі можна поділити на вільні і невільні. Вільним називається тіло, на рух якого в просторі не накладено ніякого обмеження. В противному разі тіло є невільним.
Тіла, які обмежують рух даного матеріального об’єк-та в просторі, називаються в’язями.
Наприклад, рух зошита обмежений площиною парти. Площина парти є в’яззю для зошита. Для парти в’яззю є підлога, яка обмежує її рух і т.д.
Якщо в’язь обмежує рух матеріального об’єкта в просто-рі, то вона з ним взаємодіє. Мірою цієї взаємодії є реакція в’язі.
Реакція в’язі – це сила, з якою в’язь діє на заданий матеріальний об’єкт.
Якщо проаналізувати сказане, то можна сформулювати таке правило:Реакція в’язі напрямлена протилежно напряму, в якому в’язь не дає змоги рухатись тілу.
Дане правило полегшує визначення напрямів реакцій в’язей. Воно також дає можливість визначити напрям реакцій інших в’язей, що не наведені.
Закони механіки, котрі в своїй основі базуються на законах Галілея–Ньютона, встановлені для вільних матеріальних об’єктів. Щоб застосувати ці закони до вивчення руху зв’яза-них матеріальних об’єктів, необхідно застосувати принцип звільнення від в’язей, відповідно до якого
Рух (рівновага) системи не зміниться, якщо відкинути в’язі, що накладені на систему, замінивши їх дію відповідними реакціями.
Цей принцип є однією з аксіом статики.
При розв’язанні задач механіки реакції в’язей зазвичай невідомі. Знаходження реакцій має те практичне значення, що, визначивши їх, ми тим самим визначаємо (згідно з законом дії та протидії) сили тиску на в’язь, тобто отримуємо вихідні дані для розрахунку міцності відповідних частин конструкції.
Вихідні положення (аксіоми) статики
Статика, як і вся теоретична механіка, базується на певних істинах (вихідних положеннях, аксіомах), які є результатом численних спостережень і експериментів і на основі яких шляхом логічних міркувань із застосуванням відповідного математичного апарату будується весь теоретичний курс.
Аксіомами статики є:
Аксіома зрівноваження двох сил.
Дві сили, прикладені до твердого тіла, зрівноважуються тільки в тому випадку, коли вони рівні за модулем і напрямлені по одній прямій у протилежні боки (рис. 14).

Рис. 14
Дану аксіому легко перевірити експериментально і згідно з нею маємо, що умовами зрівноваження двох сил ( і
і  ), котрі діють на тверде тіло, є:
), котрі діють на тверде тіло, є:
а) спільність ліній їх дії;
б) виконання векторної рівності
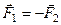 . (1.1)
. (1.1)
Аксіома приєднання і виключення зрівноваженої системи сил.
Стан твердого тіла не порушиться, якщо до системи сил, що діє на нього, приєднати або виключити систему зрівноважених сил.
Справедливість цього твердження випливає з визначення поняття “зрівноважена система сил” (див. § 4).
Наслідок.
Стан твердого тіла не порушиться при перенесенні точки прикладання сил вздовж лінії її дії в будь-яку точку тіла.
Наслідок не є аксіомою і його необхідно довести. Для доведення наслідку розглянемо тверде тіло, на яке в деякій точці  діє сила
діє сила  (рис. 15,а).
(рис. 15,а).
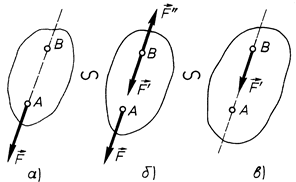
Рис. 15
Візьмемо на лінії дії сили  яку-небудь точку
яку-небудь точку  і прикладемо в цій точці дві сили
і прикладемо в цій точці дві сили 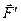 і
і  , які чисельно дорівнюють силі
, які чисельно дорівнюють силі  і задовольняють умові зрівноваження
і задовольняють умові зрівноваження  (рис. 15,б). Таке приєднання у відповідності до аксіоми 2 не порушує стану тіла, тобто система сил
(рис. 15,б). Таке приєднання у відповідності до аксіоми 2 не порушує стану тіла, тобто система сил  буде еквівалентна вихідній системі сил
буде еквівалентна вихідній системі сил  . Оскільки сили
. Оскільки сили  і
і  взаємно зрівноважуються (аксіома 1), їх, не порушуючи стану тіла, можна відкинути і одержимо одну силу
взаємно зрівноважуються (аксіома 1), їх, не порушуючи стану тіла, можна відкинути і одержимо одну силу 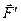 , яка прикладена в точці
, яка прикладена в точці  (рис. 15,в). Оскільки
(рис. 15,в). Оскільки 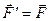 , то можна вважати, що сила
, то можна вважати, що сила 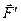 є силою
є силою  , яка перенесена вздовж лінії дії з точки
, яка перенесена вздовж лінії дії з точки  в точку
в точку  . Отже, наслідок доведений.
. Отже, наслідок доведений.
Доведене положення дає можливість, не порушуючи стану абсолютно твердого тіла, переносити сили, прикладені до нього, вздовж їх ліній дії в будь-які точки тіла.
Виходячи з класифікації векторів (вільний, невільний, ковзний), сила в статиці належить до ковзних векторів.
Аксіома дії і протидії (ІІІ-ій закон Ньютона).
Кожна механічна дія супроводжується рівною і про-тилежно напрямленою протидією.
Якщо дію позначити  , а протидію
, а протидію 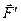 , то третя аксіома виражається такою векторною рівністю:
, то третя аксіома виражається такою векторною рівністю:
 . (1.2)
. (1.2)
Оскільки дія і протидія прикладені до різних матеріальних об’єктів, то векторна рівність (1.2) не означає, що вони взаємно зрівноважені, адже аксіома і не вимагає, щоб сили були прикладені до одного і того ж тіла.
Треба відзначити також, що хоча третя аксіома говорить про механічну взаємодію, вона справедлива для більшості (а, можливо, і для всіх) взаємодій, які є в природі.
Аксіома накладання додаткових в’язей.
Рівновага матеріального об’єкта не порушиться при накладанні на нього додаткових в’язей.
Наприклад, рівновага парти (стола) не порушиться, якщо її ніжки прикріпити до підлоги болтами.
Частковим випадком даної аксіоми є твердження:
Рівновага деформованого тіла не порушиться при його твердінні.
Це твердження часто називають принципом затвердіння.
З цього принципу випливає, що умови рівноваги для твердого тіла є необхідними (але не достатніми!) умовами рівноваги деформованого тіла.
Аксіома паралелограма.
Складання за правилом паралелограма в математиці називається векторною (геометричною) сумою і записується так: . (1.3) Рис. 16 Рис. 17Три непаралельні сили, які діють на тверде тіло в одній площині, зрівноважуються тільки в тому випадку, коли лінії їх дії перетинаються в одній точці.
Доведення. Нехай на тверде тіло в точках  ,
,  ,
, 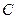 діють три непаралельні сили
діють три непаралельні сили  , які розміщені в площині рисунка (рис. 18, а, де вказані тільки сили
, які розміщені в площині рисунка (рис. 18, а, де вказані тільки сили  і
і  і точки їх прикладання).
і точки їх прикладання).

Рис. 18
Знаходимо точку перетину ліній дій сил  і
і  (точку
(точку  ) і перенесемо дані сили в точку
) і перенесемо дані сили в точку  (адже сила – це ковзний вектор). Згідно з аксіомою 5 знаходимо їх рівнодійну
(адже сила – це ковзний вектор). Згідно з аксіомою 5 знаходимо їх рівнодійну 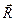 (рис. 18, б). Таким чином, на тверде тіло тепер діють тільки дві сили: знайдена рівнодійна
(рис. 18, б). Таким чином, на тверде тіло тепер діють тільки дві сили: знайдена рівнодійна 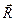 і сила
і сила  , яка ще не вказана на рисунку. Згідно з теоремою, яка доводиться, сили повинні бути зрівноважені, отже (аксіома 1) сили
, яка ще не вказана на рисунку. Згідно з теоремою, яка доводиться, сили повинні бути зрівноважені, отже (аксіома 1) сили 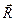 і
і  повинні мати спільну лінію дії, тоді точка прикладання
повинні мати спільну лінію дії, тоді точка прикладання  (точка
(точка 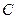 ) знаходиться на лінії дії сили
) знаходиться на лінії дії сили 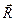 , а саме сила
, а саме сила  діє на тверде тіло, як вказано на рис. 18, в. Таким чином, лінії дії трьох сил перетинаються в одній точці.
діє на тверде тіло, як вказано на рис. 18, в. Таким чином, лінії дії трьох сил перетинаються в одній точці.
Однак треба відзначити, що теорема про три сили є тільки необхідною умовою зрівноваження трьох сил. Її часто використовують для визначення лінії дії реакції в’язі, напрям якої згідно з класифікацією в’язей невідомий.
Приклад. Визначити лінію дії реакції циліндричного шарніра  , навколо якого може обертатись однорідний стрижень
, навколо якого може обертатись однорідний стрижень 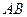 вагою
вагою 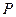 , що опирається на ребро
, що опирається на ребро  (рис. 19, а).
(рис. 19, а).

Рис. 19
Стрижень 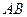 знаходиться в рівновазі. На нього діють тільки три сили: 1) сила ваги
знаходиться в рівновазі. На нього діють тільки три сили: 1) сила ваги 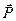 , яка прикладена в середині стрижня і напрямлена по вертикалі вниз; 2) реакція ребра
, яка прикладена в середині стрижня і напрямлена по вертикалі вниз; 2) реакція ребра  –
–  , яка перпендикулярна до поверхні стрижня; 3) реакція шарніра
, яка перпендикулярна до поверхні стрижня; 3) реакція шарніра  –
– 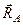 , яка невідома за напрямом. Напрям залежить від дії прикладених сил, тобто є невідомим. Але лінію дії
, яка невідома за напрямом. Напрям залежить від дії прикладених сил, тобто є невідомим. Але лінію дії 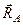 легко визначити за теоремою про три сили. Для цього знаходимо точку перетину ліній дій сил
легко визначити за теоремою про три сили. Для цього знаходимо точку перетину ліній дій сил 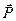 і
і  – точку
– точку  . У відповідності до доведеної теореми реакція
. У відповідності до доведеної теореми реакція 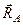 буде напрямлена по прямій
буде напрямлена по прямій  , бо для рівноваги трьох сил необхідно, щоб лінії їх дії перетинались в одній точці. В який бік? Це вже інше питання, на яке поки що відповісти не можемо. Для цього потрібно знати не тільки необхідну, а й достатню умову зрівноваження трьох сил.
, бо для рівноваги трьох сил необхідно, щоб лінії їх дії перетинались в одній точці. В який бік? Це вже інше питання, на яке поки що відповісти не можемо. Для цього потрібно знати не тільки необхідну, а й достатню умову зрівноваження трьох сил.
Розглянуті аксіоми, а також основні поняття статики дають змогу приступити до розв’язання основних задач статики для найпростішої системи сил – системи збіжних сил.
Система збіжних сил
Система збіжних сил – це система сил, лінії дії яких перетинаються в одній точці.
Зведення системи збіжних сил до канонічного вигляду
На основі аксіоми паралелограма сил проведемо послідовне додавання сил (див. рис. 20 в, де для наочності додавання проведено за правилом… (а) (індекс в позначенні рівнодійної відповідає кількості доданих сил).Рис. 20
Канонічним виглядом системи збіжних сил є одна сила (рівнодійна)
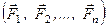
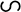
 . (1.5)
. (1.5)
До того ж, як видно з векторної рівності (в), рівнодійна системи збіжних сил дорівнює геометричній сумі всіх сил системи
 . (1.6)
. (1.6)
Векторний багатокутник  (рис. 20 в), отриманий при складанні сил, в теоретичній механіці називається силовим.
(рис. 20 в), отриманий при складанні сил, в теоретичній механіці називається силовим.
На основі векторної рівності (1.6) можна встановити два способи визначення рівнодійної.
Геометричний спосіб визначення рівнодійної.
Щоб геометрично (шляхом однієї побудови) визначити рівнодійну, необхідно скласти всі сили, тобто побудувати силовий багатокутник (рис. 20 г). Зауважимо, що додавання сил можна проводити в будь-якій послідовності. Замикаюча сторона силового багатокутника, яка напрямлена проти його обходу, визначає рівнодійну як за величиною, так і за напрямом (рис. 20 г).
Аналітичний спосіб визначення рівнодійної.
Спроектувавши рівність (1.6) на координатні осі, які вказані на рис. 20 г, отримаємо ; ; . (1.7) Формули (1.7) визначають проекції рівнодійної системи сил на декартові осі координат. В даних формулах , , – проекції…Проекція рівнодійної системи сил на вісь дорівнює алгебраїчній сумі проекцій всіх сил системи на дану вісь.
Оскільки формули (1.7) визначають проекції рівнодійної на три взаємно перпендикулярні осі, то модуль її обчислюється за формулою
 . (1.8)
. (1.8)
Напрям вектора рівнодійної визначається кутами, які утворює вектор з координатними осями. З визначення поняття “проекція на вісь” (див. додаток 2) маємо



 ;
;  ;
;  . (1.9)
. (1.9)
Формули (1.9) визначають напрямні косинуси вектора рівнодійної, а сукупність формул (1.7)–(1.9) аналітично визначає вектор рівнодійної.
Умови і рівняння рівноваги системи збіжних сил
За визначенням зрівноваженої системи сил маємо
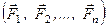
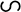
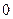 . (а)
. (а)
Для системи збіжних сил (див. 1.5) отримали
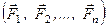
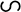
 . (б)
. (б)
Порівнюючи еквівалентності (а) і (б), отримаємо:
Для рівноваги системи збіжних сил необхідно і достатньо, щоб її рівнодійна дорівнювала нулеві
 . (1.10)
. (1.10)
Векторна рівність (1.10) є необхідною і достатньою умовою рівноваги системи збіжних сил. З даної умови випливає:
Геометрична умова рівноваги.
Як відомо, рівнодійна – це замикаюча сторона силового багатокутника (рис. 20 г). Отже, умова (1.10) буде виконуватись тільки тоді, коли остання вершина силового багатокутника суміститься з першою вершиною, тобто силовий багатокутник буде замкнутим.
Таким чином,
Необхідною і достатньою умовою рівноваги системи збіжних сил (рис. 20 в) є замкнутість її силового багатокутника (рис. 20 є).
Аналітичні умови рівноваги. Рівняння рівноваги.
Згідно з формулою (1.8), котра визначає модуль рівнодійної, умова (1.10) буде виконуватись тільки тоді, коли  ,
, 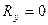 ,
,  , а це означає (див. формулу 1.7), що
, а це означає (див. формулу 1.7), що
Для рівноваги системи збіжних сил необхідно і достатньо, щоб суми проекцій цих сил на три взаємно перпендикулярні осі дорівнювали нулеві
 ;
;  ;
;  . (1.11)
. (1.11)
Очевидно, для плоскої системи збіжних сил матимемо
 ;
;  . (1.12)
. (1.12)
Таким чином, для системи збіжних сил умова рівноваги (1.10) має дві форми: геометричну – це замкнутий силовий багатокутник і аналітичну – це виконання рівності (1.11). Отже, задачі на рівновагу системи збіжних сил можна розв’язу-вати двома способами – геометрично і аналітично. Перший спосіб зручний для плоскої системи збіжних сил.
Аналітичні умови рівноваги (1.11) чи (1.12) розписані для конкретної задачі, в які входять невідомі параметри (реакції в’язей, активні сили, відстані, кути і т. ін.), називаються рівняннями рівноваги.
Алгоритм розв’язання задач на рівновагу
Всі задачі на рівновагу матеріального об’єкта, незважаючи на те, яка система діє на нього, бажано розв’язувати за таким алгоритмом.
1. Виділити матеріальний об’єкт (точку, тверде тіло, систему твердих тіл), рівновага якого буде розглядатись.
2. До виділеного матеріального об’єкта прикласти всі активні сили.
3. Користуючись принципом звільнення від в’язей, відкинути в’язі, які накладені на виділений об’єкт, замінивши їх дію відповідними реакціями.
4. Залежно від отриманої системи сил вибрати відповідні умови рівноваги.
5. Скласти рівняння рівноваги.
6. З отриманих рівнянь знайти шукані величини.
(Див. додаток 3, в якому розглянуті відповідні приклади.)
Питання для самоконтролю
1. Яка система сил називається збіжною?
2. До якого канонічного вигляду зводиться збіжна система сил?
3. Сформулюйте необхідну і достатню умову рівноваги збіжної системи сил.
4. Запишіть аналітичні умови рівноваги просторової системи збіжних сил.
5. Сформулюйте геометричну умову рівноваги системи збіжних сил.
6. Запишіть аналітичні умови рівноваги плоскої системи збіжних сил.
7. Сформулюйте теорему про три сили.
8. За теоремою про три сили вкажіть лінію реакції циліндричного шарніра  (рис. А).
(рис. А).
9. Визначіть величину рівнодійної двох рівних за модулем сил  Н, які прикладені до однієї точки, утворюючи між собою кут 60°.
Н, які прикладені до однієї точки, утворюючи між собою кут 60°.
10. Визначіть величину і напрям рівнодійної системи сил (рис. Б), якщо  Н,
Н,  Н.
Н.
11. Для системи збіжних сил  ,
, 
 ,
,  визначіть величину і напрям рівнодійної.
визначіть величину і напрям рівнодійної.
 Рис. А
Рис. А
|  Рис. Б
Рис. Б
|
12. Кут між силами 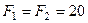 Н, які прикладені до однієї точки, дорівнює 120°. Визначіть модуль сили
Н, які прикладені до однієї точки, дорівнює 120°. Визначіть модуль сили  , яка зрівноважить задані сили.
, яка зрівноважить задані сили.
13. Вздовж діагоналі куба діє сил 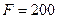 Н. Визначіть її проекції на координатні осі, початок яких знаходиться в точці прикладання сили і які напрямлені вздовж ребер куба.
Н. Визначіть її проекції на координатні осі, початок яких знаходиться в точці прикладання сили і які напрямлені вздовж ребер куба.
Теорія моменту сил
Практика підказує, що коли силу прикласти до твердого тіла, котре має закріплену точку або вісь обертання, то під дією даної сили тіло почне обертатись. Обертальна дія сили на тіло характеризується її моментом, а тому введемо нові поняття: момент сили відносно точки, момент сили відносно осі.
Момент сили відносно точки
Нехай нам задано силу  , яка прикладена в точці
, яка прикладена в точці  , і якась інша точка
, і якась інша точка  , котра не знаходиться на лінії дії сили (рис. 21, а).
, котра не знаходиться на лінії дії сили (рис. 21, а).
Введемо поняття алгебраїчного і векторного моменту сили  відносно точки
відносно точки  .
.
Алгебраїчним моментом сили відносно точки назива-ється добуток, взятий з відповідним знаком, модуля сили на її плече.
Якщо позначити момент сили відносно точки , то згідно з визначенням і рис. 21, б маємо . (1.13) Формула (1.13) визначає момент сили відносно точки. Як в даній формулі вибираються знаки? Кожна наука цей знак вибирає…Рис. 21
З’єднаємо точку  з початком і кінцем вектора сили
з початком і кінцем вектора сили  . Отримаємо трикутник
. Отримаємо трикутник  . Оскільки
. Оскільки  , а
, а 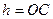 , то
, то  . Отже,
. Отже,
Момент сили відносно точки чисельно дорівнює подвійній площі трикутника, вершинами якого є точка і початок та кінець сили
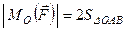 . (1.14)
. (1.14)
Формула (1.13), яка визначає момент сили відносно точки, має суттєвий недолік – вона не враховує положення площини трикутника  (рис. 21, г), від якого залежить обертальна дія сили. Адже, як показує детальний аналіз, під дією сили
(рис. 21, г), від якого залежить обертальна дія сили. Адже, як показує детальний аналіз, під дією сили  (рис. 21, д) тіло фактично намагається повернутись навколо осі, яка перпендикулярна до площини, що проходить через силу і точку. Отже, щоб повністю охарактеризувати дію сили на тверде тіло, яке має закріплену точку, бажано для визначення моменту сили відносно точки мати формулу, яка враховувала б величину сили, її плече (це враховує формула 1.13) і яка вказувала б вісь, навколо якої намагається повернутися тіло.
(рис. 21, д) тіло фактично намагається повернутись навколо осі, яка перпендикулярна до площини, що проходить через силу і точку. Отже, щоб повністю охарактеризувати дію сили на тверде тіло, яке має закріплену точку, бажано для визначення моменту сили відносно точки мати формулу, яка враховувала б величину сили, її плече (це враховує формула 1.13) і яка вказувала б вісь, навколо якої намагається повернутися тіло.
А тому введемо поняття векторного моменту (вектор-моменту) сили відносно точки.
Векторний момент сили відносно точки – це вектор, перпендикулярний до площини, котра проходить через силу і точку, і напрямлений в бік, звідки видно, що сила намагається повернути тіло проти руху годинникової стрілки (рис. 21, е).
Величина цього вектора дорівнює
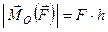 .
.
Легко отримати формулу, яка визначає вектор моменту сили 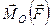 відносно точки. Для цього проведемо вектор
відносно точки. Для цього проведемо вектор 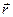 (див. рис. 21, є) з центра
(див. рис. 21, є) з центра  в точку
в точку  , в якій прикладено силу
, в якій прикладено силу  . Цей вектор, який визначає положення однієї точки відносно другої, надалі будемо називати радіус-вектором. З трикутника
. Цей вектор, який визначає положення однієї точки відносно другої, надалі будемо називати радіус-вектором. З трикутника 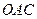 (рис. 21, є) видно, що
(рис. 21, є) видно, що
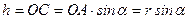 .
.
Тоді
 . (а)
. (а)
Враховуючи, що  і
і 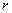 – модулі відповідних векторів, а
– модулі відповідних векторів, а 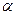 – кут між ними, формула (а) визначає модуль векторного добутку векторів
– кут між ними, формула (а) визначає модуль векторного добутку векторів  і
і 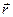 , тобто
, тобто
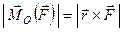 . (б)
. (б)
Порядок перемноження векторів у формулі (б) вибрано на основі властивостей векторного добутку. Відкинувши в формулі (б) модуль, отримаємо формулу, яка визначає вектор моменту сили відносно точки і враховує всі фактори, від яких залежить обертальна дія сили: величину сили, її точку прикладання, положення сили відносно точки
 . (1.15)
. (1.15)
Отже,
Вектор моменту сили відносно точки (центра) геометрично дорівнює векторному добутку радіуса-вектора точки прикладання сили відносно центра на вектор сили.
Алгебраїчним моментом сили відносно точки користуються при дії на механічну систему плоскої системи сил, векторним – у випадку дії просторової системи сил.
Момент сили відносно осі
Момент сили відносно осі – це алгебраїчна величина, яка дорівнює алгебраїчному моменту проекції сили на площину, перпендикулярну до осі, відносно точки перетину осі з площиною: .
Отже, щоб визначити момент сили  відносно осі
відносно осі  (рис. 22, а), необхідно:
(рис. 22, а), необхідно:
1. Провести площину, перпендикулярну до осі (на рис. 22, б такою площиною є площина 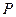 , а точка
, а точка  – це точка перетину осі з площиною).
– це точка перетину осі з площиною).

Рис. 22
2. Вектор сили  спроектувати на задану площину. Як відомо (див. додаток 1), проекція сили на площину – це вектор. В даному випадку (рис. 22, б) – це вектор
спроектувати на задану площину. Як відомо (див. додаток 1), проекція сили на площину – це вектор. В даному випадку (рис. 22, б) – це вектор  .
.
3. Отриману проекцію 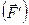 помножити на найкоротшу відстань від точки перетину осі з площиною до лінії дії цієї проекції і вибрати відповідний знак
помножити на найкоротшу відстань від точки перетину осі з площиною до лінії дії цієї проекції і вибрати відповідний знак
 . (1.16)
. (1.16)
Знак вибирається згідно з означенням алгебраїчного моменту сили 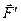 або з таких міркувань: якщо, дивлячись з кінця осі, спостерігач бачить намагання сили повернути площину проти руху годинникової стрілки, то береться знак “+”; в протилежному випадку – знак “–“. В нашому випадку (рис. 22) треба брати знак “+”.
або з таких міркувань: якщо, дивлячись з кінця осі, спостерігач бачить намагання сили повернути площину проти руху годинникової стрілки, то береться знак “+”; в протилежному випадку – знак “–“. В нашому випадку (рис. 22) треба брати знак “+”.
З формули (1.16) випливає, що момент сили відносно осі дорівнює нулеві в двох випадках:
1)  , а це буде тоді, коли сила паралельна до осі (рис. 23, а);
, а це буде тоді, коли сила паралельна до осі (рис. 23, а);
2)  – лінія дії сили проходить через вісь (рис. 23, б).
– лінія дії сили проходить через вісь (рис. 23, б).
Треба також відзначити, що момент сили відносно осі – це скалярна величина, яка графічно зображується у вигляді відрізка, котрий відкладається вздовж осі. Якщо 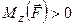 , то цей відрізок відкладається в додатному напрямі осі (рис. 23, в), при
, то цей відрізок відкладається в додатному напрямі осі (рис. 23, в), при  – у від’ємному її напрямі (рис. 23, г).
– у від’ємному її напрямі (рис. 23, г).

Рис. 23
Оскільки( див. рис. 22, в)  є основою трикутника
є основою трикутника 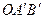 , а
, а 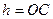 – його висота, то
– його висота, то  і отримуємо
і отримуємо
 , (1.17)
, (1.17)
Момент сили відносно осі чисельно дорівнює подвійній площі трикутника, вершинами якого є початок і кінець вектора проекції сили на площину, перпендикулярну до осі, і точка перетину осі з пло-щиною (рис. 22, в).
Залежність між моментом сили відносно точки і моментом сили відносно осі, яка проходить через цю точку
. (а)Рис. 24
Вказуємо цей вектор на рисунку (див. рис. 24, б). Тепер визначимо момент сили  відносно осі. Для цього силу
відносно осі. Для цього силу  спроектуємо на площину
спроектуємо на площину 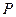 , яка проходить через точку
, яка проходить через точку  перпендикулярно до осі
перпендикулярно до осі  . Отримаємо вектор
. Отримаємо вектор 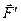 . Як було встановлено, момент сили відносно осі – це скалярна величина, яка чисельно визначається за формулою (див. 1.17)
. Як було встановлено, момент сили відносно осі – це скалярна величина, яка чисельно визначається за формулою (див. 1.17)
 . (б)
. (б)
З рисунка 24, б видно, що трикутник 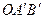 є проекцією трикутника
є проекцією трикутника  на площину
на площину 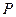 . З математики відомо, що площа проекції плоскої фігури на площину
. З математики відомо, що площа проекції плоскої фігури на площину  дорівнює площі фігури
дорівнює площі фігури  , помноженій на косинус кута між площинами фігури і проекції, тобто
, помноженій на косинус кута між площинами фігури і проекції, тобто
 . (в)
. (в)
Застосувавши рівність (в) до трикутників 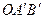 і
і  і помноживши обидві її частини на 2, дістанемо
і помноживши обидві її частини на 2, дістанемо
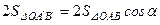 ,
,
або
 . (г)
. (г)
В отриманій залежності 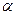 – це кут між площинами трикутників
– це кут між площинами трикутників  і
і 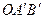 . Але кут між двома площинами дорівнює гострому куту між перпендикулярами до цих площин.
. Але кут між двома площинами дорівнює гострому куту між перпендикулярами до цих площин.
Якщо ввести кут між векторним моментом 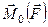 і додатним напрямом осі
і додатним напрямом осі  , то з врахуванням формули (г) можна записати
, то з врахуванням формули (г) можна записати

 . (1.18)
. (1.18)
Рівність (1.18) дає залежність між моментом сили відносно точки і моментом сили відносно осі, котра проходить через задану точку, згідно з якою маємо:
Момент сили відносно осі дорівнює проекції вектора моменту сили відносно точки, що знаходиться на осі, на задану вісь.
Отже, ми отримали ще один спосіб визначення моменту сили відносно осі. Згідно з цим способом, необхідно визначити вектор моменту сили відносно будь-якої точки даної осі і отриманий вектор спроектувати на цю вісь. Даний спосіб в практиці майже не використовується, бо момент сили відносно осі найлегше визначити за формулою (1.16). Зате в теоретичному курсі він часто використовується.
Аналітичне визначення моменту сили відносно довільної точки
.Рис. 25
З векторної алгебри відомо, що кожний векторний добуток можна представити у вигляді визначника. В нашому випадку
 .
.
Розкривши визначник за елементами першого рядка, отримаємо
 , (а)
, (а)
де 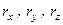 – проекції радіус-вектора
– проекції радіус-вектора 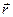 на координатні осі.
на координатні осі.
Згідно з рис. 25 маємо 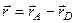 , отже
, отже
 (б)
(б)
Сам вектор  можна розкласти вздовж осей координат
можна розкласти вздовж осей координат
 . (в)
. (в)
Співставляючи рівності (а) і (в) і враховуючи (б), отримаємо
 , (1.19)
, (1.19)
Формули (1.19) визначають проекції на декартові осі координат вектора моменту сили відносно точки  .
.
Знаючи проекції, за формулою
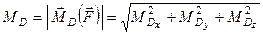 (1.20)
(1.20)
легко обчислюється модуль вектора моменту відносно точки  . Напрямні косинуси вектора
. Напрямні косинуси вектора  дорівнюють
дорівнюють


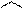
 (1.21)
(1.21)
Отримані формули (1.19)–(1.21) аналітично визначають вектор моменту сили відносно довільної точки  з координатами
з координатами  . Якщо точка
. Якщо точка  збігається з початком координат
збігається з початком координат  , тоді
, тоді  , і формули (1.19) набувають вигляду
, і формули (1.19) набувають вигляду
 (1.22)
(1.22)
Формули (1.22) визначають проекції на координатні осі вектора моменту сили відносно початку координат. Дані формули мають і другий зміст – вони визначають момент сили відносно координатних осей, адже у відповідності з формулою (1.18) проекція вектора моменту сили відносно точки на вісь, яка проходить через дану точку, дорівнює моменту цієї сили відносно даної осі.
Теорема Варіньйона
Доведення.Сформульована теорема справедлива для будь-якої системи сил, яка має рівнодійну. Доведення теореми проведемо лише для збіжної системи сил,… Нехай сили даної системи прикладені до точки (рис. 26). До цієї ж точки буде прикладена і рівнодійна заданої системи сил. Визначимо її момент відносно довільної точки . З…Алгебраїчний момент рівнодійної плоскої системи сил відносно довільної точки, яка знаходиться в площині дії сил, дорівнює алгебраїчній сумі моментів складових сил відносно даної точки.
3. Теорема Варіньйона має широке практичне використання. На практиці її використовують там, де визначення моменту сили ускладнене через трудність визначення її плеча. У цих випадках діють так: силу розкладають на складові, для яких легко визначаються плечі, і момент даної сили визначають як суму моментів її складових.
Приклад. Визначити момент сили 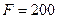 Н (див.
Н (див.
рис. 27) відносно точки  , якщо
, якщо  м,
м,  м.
м.
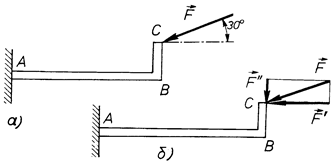
Рис. 27
Розв’язання. Для визначення моменту сили  відносно точки
відносно точки  розкладемо її на складові
розкладемо її на складові 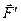 і
і  (див. рис. 27, б), причому
(див. рис. 27, б), причому
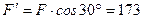 Н;
Н;
 Н.
Н.
Момент сили  відносно точки
відносно точки  визначимо як суму моментів її складових
визначимо як суму моментів її складових

 Н×м.
Н×м.
Питання для самоконтролю
1. Що називається моментом сили відносно точки?
2. Запишіть формулу, за допомогою якої визначається алгебраїчний момент сили відносно точки.
3. Чому прийнято момент сили відносно точки вважати вектором?
4. Який напрям має вектор моменту сили відносно точки?
5. Запишіть формулу, яка визначає вектор моменту сили відносно точки.
6. Визначіть момент сили  відносно точки
відносно точки  , якщо
, якщо 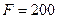 Н,
Н,  м. (рис. А).
м. (рис. А).
7. Що називається моментом сили відносно осі?
 Рис. А
Рис. А
| 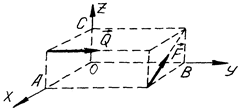 Рис. Б
Рис. Б
|
8. Запишіть формулу, за допомогою якої визначається момент сили відносно осі.
9. В яких випадках момент сили відносно осі дорівнює нулеві?
10. Як графічно зобразити момент сили відносно осі?
11. Визначіть моменти сил  і
і  відносно координатних осей, якщо
відносно координатних осей, якщо  кН,
кН,  кН,
кН,  м,
м, 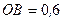 м,
м,  м. (рис. Б).
м. (рис. Б).
12. Запишіть формулу, яка відображає залежність між моментом сили відносно точки і моментом сили відносно осі, що проходить через задану точку.
13. Визначіть величину моменту сили  відносно початку осей координат, якщо задана сила прикладена в точці
відносно початку осей координат, якщо задана сила прикладена в точці 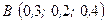 . Проекції сили на координатні осі задані в Ньютонах, а координати точки В – в метрах.
. Проекції сили на координатні осі задані в Ньютонах, а координати точки В – в метрах.
Довільна система сил
Перш ніж приступити до розв’язання основних задач теоретичного курсу статики для довільної системи сил введемо додаткові поняття.
Головний вектор і головний момент системи сил
Поняття головного вектора і головного моменту системи сил є одним з основних понять теоретичної механіки. Це пояснюється, як Ви переконаєтесь в процесі вивчання теоретичного курсу, тим, що дія системи сил на тверде тіло визначається значенням її головного вектора і головного моменту.
Нехай задано довільну систему сил  , які прикладені відповідно в точках
, які прикладені відповідно в точках  (рис. 28, а).
(рис. 28, а).
Головним вектором системи сил називається геометрична сума всіх сил системи
 . (1.26)
. (1.26)
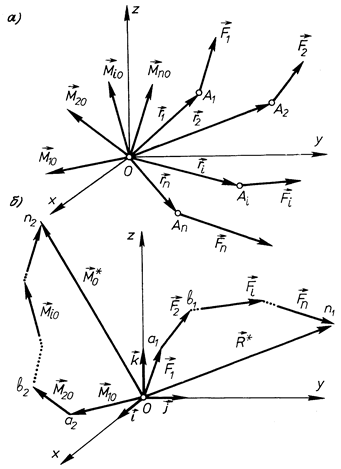
Рис. 28
До точок прикладання сил з центра  проведемо радіус-вектори
проведемо радіус-вектори  (рис. 28, а) і за формулою (1.13) визначимо момент кожної сили відносно центра
(рис. 28, а) і за формулою (1.13) визначимо момент кожної сили відносно центра  .
.
Головним моментом системи сил відносно довільної точки називається геометрична сума векторних моментів всіх сил системи відносно даної точки
 . (1.27)
. (1.27)
На основі формул (1.26–1.27) можна вказати два способи визначення головного вектора і головного моменту системи сил.
Геометричний спосіб
Щоб геометрично визначити головний вектор, необхідно векторно скласти всі сили системи, тобто побудувати силовий багатокутник  (рис. 28, б). Замикаюча сторона силово-го багатокутника, напрямлена проти його обходу, визначає як величину, так і напрям головного вектора заданої системи сил.
(рис. 28, б). Замикаюча сторона силово-го багатокутника, напрямлена проти його обходу, визначає як величину, так і напрям головного вектора заданої системи сил.
Аналогічно визначається і головний момент системи сил. Тільки тут будується багатокутник моментів  (рис. 28, в).
(рис. 28, в).
Аналітичний спосіб
(1.28) (1.29) Формули (1.28) визначають проекції головного вектора на декартові осі… Формули (1.29) визначають проекції головного моменту системи сил на декартові осі координат. В даних формулах –…Пара сил і її момент
Система двох рівних за величиною протилежно напря-млених сил (), лінії дії яких не співпадають, називається парою сил (рис. 29).
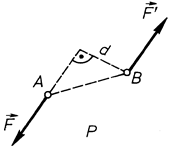 Рис. 29
Рис. 29
|  Рис. 30
Рис. 30
|
Основними характеристиками пари сил є:
1. Площина дії пари сил – це площина, в якій знаходиться пара сил. На рис. 29, на якому зображено пару сил  ,
, 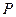 – це площина дії заданої пари сил. Вона єдина, оскільки через дві паралельні лінії можна провести тільки одну площину.
– це площина дії заданої пари сил. Вона єдина, оскільки через дві паралельні лінії можна провести тільки одну площину.
2. Плече пари сил – це найкоротша відстань між лініями дії сил пари. На рис. 29 воно позначено літерою 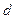 .
.
3. Момент пари сил.
Для введення поняття моменту пари сил розглянемо пару сил  , сили якої прикладені в точках
, сили якої прикладені в точках  і
і  (рис. 30). Виберемо довільну точку
(рис. 30). Виберемо довільну точку  і проведемо відповідні радіуси-вектори
і проведемо відповідні радіуси-вектори  . За формулою (1.26) визначимо головний вектор пари сил
. За формулою (1.26) визначимо головний вектор пари сил
 .
.
Отже, головний вектор пари сил дорівнює нулеві.
За формулою (1.27) визначимо головний момент пари сил відносно довільної точки 
 .
.
Оскільки  , отримаємо
, отримаємо
 ,
,
тобто:
 .
.
Головний момент пари сил не залежить від положення точки, відносно якої він визначається, а залежить тільки від параметрів самої пари сил і називається моментом пари сил.
Отже,
Момент пари сил дорівнює векторному моменту однієї сили пари відносно точки прикладання іншої сили даної пари, тобто
 . (1.34)
. (1.34)
З отриманого випливає:
1. Момент пари сил – це вектор, бо вектором є момент сили відносно точки.
2. Вектор моменту пари сил перпендикулярний до площини дії пари, оскільки вектор  перпендикулярний до площини, яка проходить через точку
перпендикулярний до площини, яка проходить через точку  і вектор сили
і вектор сили  , а це є площина дії пари сил.
, а це є площина дії пари сил.
3. Якщо побудувати вектор  (рис. 31, а), а це згідно з формулою (1.34) буде вектор моменту пари сил, то ми отримаємо, що момент пари сил як вектор напрямлений в бік, звідки спостерігач бачить намагання пари сил повернути тіло проти руху годинникової стрілки.
(рис. 31, а), а це згідно з формулою (1.34) буде вектор моменту пари сил, то ми отримаємо, що момент пари сил як вектор напрямлений в бік, звідки спостерігач бачить намагання пари сил повернути тіло проти руху годинникової стрілки.

Рис. 31
Визначимо величину вектора моменту пари сил. За формулою (1.34) маємо
 .
.
Оскільки (див. рис. 31, б)
 ,
,
отримуємо
 . (а)
. (а)
Отже,
Момент пари сил чисельно дорівнює добутку модуля однієї сили пари на її плече.
Якщо пари сил розміщені в одній площині, то величини їх моментів знаходяться за формулою (a), а вектори цих моментів будуть колінеарними. В цьому випадку доцільніше користуватися не векторним поняттям моменту пари сил, а алгебраїчним.
Алгебраїчний момент пари сил дорівнює добутку, взятому з відповідним знаком, модуля однієї сили пари на її плече, тобто
 . (1.35)
. (1.35)
Той чи інший знак у цій формулі визначається за таким правилом: якщо спостерігач бачить намагання пари сил повернути тіло проти годинникової стрілки, береться знак “+”, в противному разі – знак “–“.
Алгебраїчні моменти пари сил на рисунках показують дуговими стрілками (рис. 32).
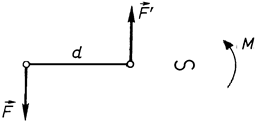
Рис. 32
Зазначимо, що одиницею виміру моменту пари сил, як і моменту сили, є Н×м.
Еквівалентність пар сил
Тут будуть тільки сформульовані (без відповідних доведень) теореми, які нададуть нам можливість виконувати певні дії над парами сил. З доведенням даних теорем можна ознайомитись в додатку 4.
Теорема 1.
Дія пари сил на тверде тіло не зміниться, якщо пару сил в площині її дії перемістити в будь-яке положення (рис. 33).

Рис. 33
Теорема 2.
Дія пари сил на тверде тіло не зміниться, якщо пару сил перемістити в площину, яка паралельна площині дії пари сил (рис. 34).
Теорема 3.
Дія пари сил на тверде тіло не зміниться, якщо змі-нити сили пари і плече пари, залишивши без змін момент пари.
Для пар сил, показаних на рис. 35, 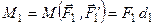 і
і  . З рівності
. З рівності  випливає, що для еквівалентних пар сили обернено пропорційні їх плечам.
випливає, що для еквівалентних пар сили обернено пропорційні їх плечам.
Сформульовані три теореми можна об’єднати в одну:
Пари сил, моменти яких геометрично рівні, є еквівалентними
Рівність (1.36) є необхідною і достатньою умовою еквівалентності двох пар сил з моментами і . Рис. 34 Рис. 35 На основі сформульованих теорем бачимо, що над парою сил, як елементом статики, можна виконувати такі дії:Додавання пар сил
Теорема.
Дія пари сил, які лежать в площинах, що перетина-ються, еквівалентні одній парі сил, момент якої до-рівнює геометричній сумі моментів заданих пар сил.
Доведення. Припустимо, що задано дві пари сил  і
і  з моментами відповідно
з моментами відповідно 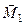 і
і  . Пари сил лежать в площинах
. Пари сил лежать в площинах 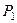 і
і 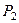 , що перетинаються.
, що перетинаються. 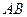 – лінія перетину цих площин (рис. 36, а).
– лінія перетину цих площин (рис. 36, а).
На основі теорем про еквівалентність пар приведемо задані пари сил до одного плеча 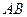 (рис. 36, б). В результаті такого приведення в точках
(рис. 36, б). В результаті такого приведення в точках  і
і  буде прикладено по дві сили:
буде прикладено по дві сили:

Рис. 36
в точці  —
—  і
і  , в точці
, в точці  —
— 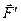 і
і 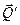 . Геометрично складемо ці сили
. Геометрично складемо ці сили
 ;
; 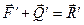 .
.
Оскільки  і
і  розглядаються як сили, що утворюють пари сил, то і
розглядаються як сили, що утворюють пари сил, то і 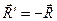 . Отже, отримані сили
. Отже, отримані сили  утворюють пару сил. Таким чином, дві пари сил замінено однією парою, яка, очевидно, є еквівалентною заданим парам, бо всі перетворення, в результаті яких вона отримана, пророблені на основі теорем про еквівалентність пар і аксіоми паралелограма сил.
утворюють пару сил. Таким чином, дві пари сил замінено однією парою, яка, очевидно, є еквівалентною заданим парам, бо всі перетворення, в результаті яких вона отримана, пророблені на основі теорем про еквівалентність пар і аксіоми паралелограма сил.
Визначимо момент 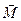 отриманої пари за формулою
отриманої пари за формулою

 .
.
Отже,
Момент еквівалентної пари дорівнює геометричній сумі моментів заданих пар
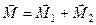 . (1.37)
. (1.37)
Розглянемо систему пар сил 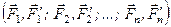 з моментами відповідно
з моментами відповідно 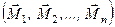 . Склавши перші дві пари, отримаємо пару сил, еквівалентну їм, з моментом
. Склавши перші дві пари, отримаємо пару сил, еквівалентну їм, з моментом
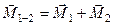 .
.
Одержану пару сил складемо з третьою і отримаємо пару сил, яка вже буде еквівалентна трьом парам сил. Її момент
 .
.
Продовживши додавання і виконавши 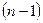 складання, отри-маємо одну пару сил з моментом
складання, отри-маємо одну пару сил з моментом
 ,
,
яка буде еквівалентною заданій системі пар сил.
Отже,
Дію на тверде тіло системи пар сил, довільно розміщених в просторі, можна замінити дією однієї пари сил, момент якої дорівнює геометричній сумі моментів всіх пар системи
 . (1.38)
. (1.38)
Іншими словами, канонічним виглядом системи пар сил є пара сил з моментом 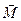 , який визначається за формулою (1.38).
, який визначається за формулою (1.38).
Якщо момент результуючої пари буде дорівнювати нулеві, то це означає, що дія системи пар сил на тверде тіло рівна нулеві, тобто система пар сил є зрівноваженою.
Таким чином,
Система пар сил, які розміщені довільно в просторі, знаходиться в рівновазі, якщо геометрична сума мо-ментів всіх пар, що утворюють систему, дорівнює нулеві
 . (1.39)
. (1.39)
Рівність (1.39) є необхідною і достатньою умовою рівноваги системи пар сил.
Спроектувавши векторну рівність (1.39) на координатні осі і пам’ятаючи, що проекція векторної суми на вісь дорівнює алгебраїчній сумі відповідних проекцій, отримаємо
 ;
;  ;
;  . (1.40)
. (1.40)
Це аналітичні умови рівноваги системи пар сил, які формулюються так:
Для рівноваги системи пар сил, які довільно розміщені в просторі, необхідно і достатньо, щоб алгебраїчні суми проекцій її моментів на три координатні осі відповідно дорівнювали нулеві.
В частковому випадку, коли системи пар сил розміщені в одній площині, а це означає, що їх вектори моментів паралельні між собою, рівності (1.38) і (1.39) набувають такого значення:
Момент пари сил, яка еквівалентна системі пар, розміщених в одній площині, дорівнює сумі алгебраїчних моментів складових пар
 ; (1.41)
; (1.41)
Система пар сил, розміщених в одній площині, знаходиться в рівновазі, якщо сума їх алгебраїчних мо-ментів дорівнює нулеві
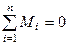 . (1.42)
. (1.42)
Лема про паралельний перенос сили
З попереднього відомо, що сила – це ковзний вектор. Це положення і аксіома паралелограма сил дали можливість звести до канонічного вигляду систему збіжних сил. Для розширення наших можливостей щодо перетворення системи сил доведемо таку просту теорему (лему):
Силу, прикладену до твердого тіла в деякій його точці, можна, не порушуючи її дії на тверде тіло, паралельно перенести в будь-яку точку тіла, якщо при цьому прикласти пару сил, момент якої векторно дорівнює моменту заданої сили відносно точки переносу.
Для доведення цієї теореми розглянемо силу  , яка при-кладена в точці
, яка при-кладена в точці  твердого тіла. Візьмемо на тілі довільну точку
твердого тіла. Візьмемо на тілі довільну точку  . Радіус-вектор точки
. Радіус-вектор точки  відносно точки
відносно точки  позначимо
позначимо 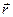 (рис. 37, а). Прикладемо в точці
(рис. 37, а). Прикладемо в точці  дві сили
дві сили  , які вза-ємно зрівноважуються і одна з них, наприклад,
, які вза-ємно зрівноважуються і одна з них, наприклад, 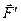 , геометрич-но дорівнює
, геометрич-но дорівнює  , тобто
, тобто 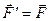 , тоді
, тоді  (рис. 37, б). Згідно з аксіомою приєднання і виключення системи зрівноважених сил отримана система сил буде еквівалентною заданій силі
(рис. 37, б). Згідно з аксіомою приєднання і виключення системи зрівноважених сил отримана система сил буде еквівалентною заданій силі 
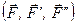
 . (а)
. (а)

Рис. 37
Оскільки сили  і
і 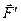 задовольняють умові
задовольняють умові 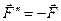 , то ці сили утворюють пару сил, дію якої на тверде тіло можна зобразити моментом
, то ці сили утворюють пару сил, дію якої на тверде тіло можна зобразити моментом 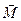 (рис. 37, в). Згідно з попереднім, момент пари сил
(рис. 37, в). Згідно з попереднім, момент пари сил 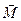 геометрично дорівнює моменту однієї сили пари (наприклад,
геометрично дорівнює моменту однієї сили пари (наприклад,  ) відносно точки прикладання іншої сили пари, тобто
) відносно точки прикладання іншої сили пари, тобто
 . (б)
. (б)
Отже,
При паралельному переносі сили () в довільну точ-ку отримуємо силу (), геометрично рівну заданій силі, і пару сил , момент якої геометрично дорівнює моменту заданої сили відносно точки переносу.
Зауважимо, що в літературі точку  , куди переноситься сила, часто називають точкою зведення, а пару сил, яка при цьому утворюється, називають приєднаною парою. Якщо точка зведення буде знаходитись на лінії дії сили, то момент приєднаної пари буде дорівнювати нулеві, отже, пари сил фактично не буде, тоді ми отримаємо тільки одну силу, тобто ще раз переконуємось, що сила – це ковзний вектор.
, куди переноситься сила, часто називають точкою зведення, а пару сил, яка при цьому утворюється, називають приєднаною парою. Якщо точка зведення буде знаходитись на лінії дії сили, то момент приєднаної пари буде дорівнювати нулеві, отже, пари сил фактично не буде, тоді ми отримаємо тільки одну силу, тобто ще раз переконуємось, що сила – це ковзний вектор.
Зведення довільної системи сил до заданого центра
Дано систему сил 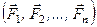 , що прикладені в точках
, що прикладені в точках  і як завгодно напрямлені в просторі (рис. 38, а). Візьмемо довільну точку
і як завгодно напрямлені в просторі (рис. 38, а). Візьмемо довільну точку  , яку назвемо центром зведення, і зведемо всі задані сили до точки
, яку назвемо центром зведення, і зведемо всі задані сили до точки  . Згідно з лемою про паралельний перенос сили отримаємо
. Згідно з лемою про паралельний перенос сили отримаємо

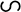
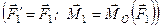 ;
;

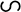
 ;
;
. . . . . . . . . . . . . . . . . .

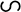
 .
.
Отже, в точці  одержано систему сил
одержано систему сил  і систему пар сил з моментами
і систему пар сил з моментами 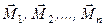 (рис. 38, б). Одержана система сил є збіжною, бо всі сили прикладені до однієї точки
(рис. 38, б). Одержана система сил є збіжною, бо всі сили прикладені до однієї точки  . Геометрично склавши ці сили, знайдемо їх рівнодійну (рис. 39)
. Геометрично склавши ці сили, знайдемо їх рівнодійну (рис. 39)
 .
.
Оскільки  , то отримаємо
, то отримаємо
 .
.

Рис. 38
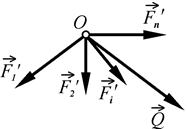 Рис. 39
Рис. 39
|  Рис. 40
Рис. 40
|
В отриманій рівності праворуч маємо геометричну суму всіх сил заданої системи, а це, як відомо (див. формулу 1.26), є її головний вектор. Отже, рівнодійна отриманої системи сил геометрично дорівнює головному вектору заданої системи сил  .
.
Систему отриманих пар сил замінимо еквівалентною парою, момент якої, як відомо з теореми про складання пар, дорівнює геометричній сумі моментів складових пар (рис. 40)
 .
.
Оскільки 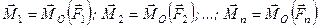 , то отримаємо
, то отримаємо
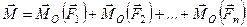 .
.
В отриманій рівності праворуч маємо геометричну суму моментів всіх сил заданої системи відносно точки  , тобто її головний момент відносно точки
, тобто її головний момент відносно точки  . Отже, момент пари сил, яка еквівалентна отриманій системі приєднаних пар, геометрично дорівнює головному моменту заданої системи відносно точки зведення
. Отже, момент пари сил, яка еквівалентна отриманій системі приєднаних пар, геометрично дорівнює головному моменту заданої системи відносно точки зведення 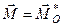 .
.
Таким чином, при зведенні довільної системи сил до заданого центра в даному центрі отримаємо одну силу, яка геометрично дорівнює головному вектору заданої системи сил, і пару сил, момент якої геометрично дорівнює головному моменту заданої системи сил відносно точки зведення (рис. 41).

Рис. 41
Тобто, систему сил, розміщених довільно в просторі, завжди можна звести до однієї сили, яка дорівнює її головному вектору і прикладена в точці зведення, і до пари сил, момент якої геометрично дорівнює головному моменту системи відносно точки зведення
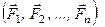

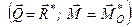 . (1.43)
. (1.43)
Окремі випадки зведення довільної системи сил
1. Головний вектор і головний момент заданої системи сил відповідно дорівнюють нулеві (1.44) В цьому випадку згідно з еквівалентністю (1.43) маємоРис. 47
Дві сили  і
і 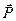 , які прикладені в точці О, взаємно зрівноважуються і їх можна виключити. Залишається сила
, які прикладені в точці О, взаємно зрівноважуються і їх можна виключити. Залишається сила 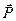 , прикладена в точці А і пара сил з моментом
, прикладена в точці А і пара сил з моментом  (рис. 47, в). Оскільки момент пари сил є вільним вектором, то перенесемо його в точку А і зобразимо його парою сил
(рис. 47, в). Оскільки момент пари сил є вільним вектором, то перенесемо його в точку А і зобразимо його парою сил  , площина дії якої перпендикулярна моменту
, площина дії якої перпендикулярна моменту 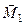 , а значить і силі
, а значить і силі 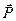 , тобто отримали динаму (рис. 47, г)
, тобто отримали динаму (рис. 47, г)
Пряма, по якій діє сила динами, називається централь-ною віссю системи.
Складемо тепер таблицю всіх можливих випадків зведення довільної системи сил до канонічного вигляду. № Значення Канонічний… Розглянемо тепер частковий випадок – плоску систему сил. Площину, в якій знаходяться сили, позначимо (рис. 48).…Рис. 48
Вектор моменту кожної сили заданої системи відносно будь-якої точки О площини дії сил буде перпендикулярним до цієї площини, тобто вони утворюють систему паралельних векторів. Тому можна сказати, що
Головний момент плоскої системи сил відносно довільної точки площини дії сил дорівнює сумі алгебраїчних моментів всіх сил системи відносно даної точки
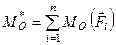 . (1.46)
. (1.46)
Напрям його перпендикулярний до площини дії сили, отже,  , тобто скалярний добуток головного вектора на головний момент плоскої системи сил завжди дорівнює нулеві:
, тобто скалярний добуток головного вектора на головний момент плоскої системи сил завжди дорівнює нулеві:  . Це означає, що плоска система сил може мати тільки три випадки зведення – звестись до нуля, тобто бути зрівноваженою; до пари сил; до рівнодійної. Плоска система сил не може звестись до динами.
. Це означає, що плоска система сил може мати тільки три випадки зведення – звестись до нуля, тобто бути зрівноваженою; до пари сил; до рівнодійної. Плоска система сил не може звестись до динами.
Інваріанти довільної системи сил
Величини, які не змінюються при певних перетвореннях, називаються інваріантами відносно даних перетво-рень.
Інваріантами довільної системи сил називаються величин, які не залежать від вибору центра зведення. Для встановлення таких величин розглянемо довільну систему сил  і виберемо дві довільні точки О1 і О2 (рис.
і виберемо дві довільні точки О1 і О2 (рис.
49, а). Звівши систему сил до центра О1, отримаємо (рис. 49, б)
 ; (а)
; (а)
 . (б)
. (б)
Якщо задану систему сил звести до центра О2, то в даній точці отримаємо (рис. 49, б)
 ; (в)
; (в)
 . (г)
. (г)

Рис. 49
В рівностях (а) і (в) справа знаходиться геометрична сума однієї і тієї ж системи сил, отже 
Головний вектор системи сил не залежить від центра зведення, тобто є інваріантом.
Якщо порівняти рівності (б) і (г), то (враховуючи, що 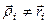 ) можна стверджувати, що головний момент системи сил взагалі залежить від центра зведення. Встановимо цю залежність. Враховуючи (див. рис. 49, а), що
) можна стверджувати, що головний момент системи сил взагалі залежить від центра зведення. Встановимо цю залежність. Враховуючи (див. рис. 49, а), що
 ,
,
отримаємо

Оскільки (див. рівність б)
 ,
,
 ,
,
то кінцево отримуємо формулу, яка відображає залежність головного моменту системи від центра зведення
 . (1.47)
. (1.47)
При зміні центра зведення головний момент системи зменшується на момент головного вектора, що прикладений в новому центрі зведення відносно старого центра.
Зауваження. В деяких підручниках у формулі (1.47) стоїть знак плюс, це пояснюється тим, що їх автори розглядають момент головного вектора, що прикладений в старому центрі зведення відносно нового центра.
Скалярно помноживши векторну рівність (1.47) на головний вектор 

і, враховуючи, що:
а) змішаний добуток  бо в ньому присутні два однакових співмножники
бо в ньому присутні два однакових співмножники  ;
;
б) головний вектор є інваріантом довільної системи сил, тобто  , отримаємо
, отримаємо
 . (1.48)
. (1.48)
Скалярний добуток головного вектора на головний момент не залежить від центра зведення, тобто є інваріантом довільної системи сил.
1. Векторний інваріант – це головний вектор довільної системи сил. 2. Скалярний інваріант – це скалярний добуток головного вектора системи сил на… За допомогою формули (1.47) можна провести загальне доведення теореми Варіньйона, яка була доведена для системи…Аналітичні умови рівноваги просторової системи сил
Вище (див. § 21) було встановлено, що необхідною і достатньою умовою зрівноваження довільної системи сил є рівність нулеві її головного вектора і головного моменту (див. рівності 1.44)
 (а)
(а)
Враховуючи, що  , рівності (а) можна записати у вигляді
, рівності (а) можна записати у вигляді
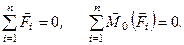 б)
б)
Проектуючи векторні рівності (б) на декартові осі координат, з врахуванням залежності (1.18) отримуємо аналітичні умови рівноваги довільної системи сил
 (1.49)
(1.49)
Отже,
Для рівноваги довільної просторової системи сил необхідно і достатньо, щоб сума проекцій всіх сил системи на три координатні осі та суми моментів всіх сил системи відносно цих координатних осей дорівнювали нулеві.
Таким чином, при розв’язуванні задач на рівновагу довільної просторової системи сил, яка прикладена до твердого тіла, необхідно скласти шість рівнянь рівноваги вигляду (1.49) і маємо можливість за їх допомогою визначити шість невідомих величин.
Розглянемо частковий випадок – просторову систему паралельних сил. Систему координат виберемо так, щоб вісь  була паралельна лініям дій сил (рис. 50). Система сил буде знаходитись в рівновазі, коли будуть виконуватись умови (1.49), бо це умова рівноваги довільної, тобто будь-якої системи сил. Оскільки розглянута система сил є спрощеним варіантом довільної системи, то і система умов (1.49) повинна спроститись. Спрощення системи (1.49) проведемо шляхом виключення рівностей, які виконуються тотожно, тобто
була паралельна лініям дій сил (рис. 50). Система сил буде знаходитись в рівновазі, коли будуть виконуватись умови (1.49), бо це умова рівноваги довільної, тобто будь-якої системи сил. Оскільки розглянута система сил є спрощеним варіантом довільної системи, то і система умов (1.49) повинна спроститись. Спрощення системи (1.49) проведемо шляхом виключення рівностей, які виконуються тотожно, тобто
фактично є зайвими. Такими рівностями, очевидно, є:
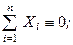
 і ми отримуємо систему
і ми отримуємо систему
 (1.50)
(1.50)
які є аналітичними умовами рівноваги просторової системи паралельних сил.

Рис. 50
Аналітичні умови рівноваги плоскої системи сил
До того ж для даної системи сил, враховуючи, що сили знаходяться в площині,… ,Рис. 51
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми проекцій всіх сил системи на дві координатні осі та суми їх моментів відносно довільної точки, яка знаходиться в площи-ні дії сил, дорівнювали нулеві.
Таким чином, для плоскої системи сил маємо три аналітичні умови, але їх можна записати в трьох формах. Якщо вва-жати (1.51) умовами рівноваги плоскої системи сил в першій формі, то другою формою її умов рівноваги є
 (1.52)
(1.52)
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми алгебраїчних моментів всіх сил системи відносно двох довільних точок А і В, що знаходяться в площині дії сил, і сума проекцій сил на будь-яку вісь Оx, що лежить в цій площині і не перпендикулярна до прямої, яка з’єднує точки А і В, дорівнювали нулеві.
Третя форма
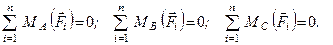 (1.53)
(1.53)
Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб суми алгебраїчних моментів всіх сил системи відносно трьох довільних точок А, В і С, які знаходяться в площині дії сил і не лежать на одній прямій, дорівнювали нулеві.
При рівновазі плоскої системи сил необхідність виконання умов (1.52) і (1.53) випливає з умов рівноваги (1.51). Доведено достатність цих умов.
В тому, що умови (1.52) і (1.53) є аналітичними умовами рівноваги плоскої системи сил, можна легко переконатися, якщо визначити головний вектор і головний момент плоскої системи сил, котра задовольняє дані умови. Для цього спочатку розглянемо плоску систему сил  , яка задовольняє умови (1.52) і зведемо дану систему до довільної точки Е (рис. 52). Згідно із загальною теорією зведення системи сил до заданого центра в точці Е отримаємо силу
, яка задовольняє умови (1.52) і зведемо дану систему до довільної точки Е (рис. 52). Згідно із загальною теорією зведення системи сил до заданого центра в точці Е отримаємо силу  , геометрично рівну головному вектору системи
, геометрично рівну головному вектору системи  , і пару сил з моментом М, котрий дорівнює головному моменту системи відносно точки зведення
, і пару сил з моментом М, котрий дорівнює головному моменту системи відносно точки зведення 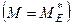 . Оскільки задана система задовольняє умові
. Оскільки задана система задовольняє умові  , то її головний вектор, отже і отримана сила, будуть перпендикулярними до осі
, то її головний вектор, отже і отримана сила, будуть перпендикулярними до осі 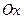 (рис. 52). На площині дії сили вибираємо дві довільні точки А і В і складемо суми моментів сил отриманої системи відносно даних точок (див. рис. 52)
(рис. 52). На площині дії сили вибираємо дві довільні точки А і В і складемо суми моментів сил отриманої системи відносно даних точок (див. рис. 52)
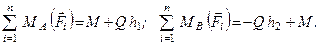
Оскільки  і відповідно до умов (1.52)
і відповідно до умов (1.52)  ;
;  , то отримаємо
, то отримаємо

Рис. 52

Звідки 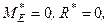 тобто розглянута система сил задовольняє необхідну і достатню умову рівноваги.
тобто розглянута система сил задовольняє необхідну і достатню умову рівноваги.
Тепер розглянемо плоску систему сил, яка задовольняє умови (1.53).Визначимо її головний вектор і головний момент. Для цього систему сил зведемо до центра Е, в якому отримаємо силу  і пару сил з моментом М, причому
і пару сил з моментом М, причому 
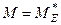 (рис. 53). В площині дії сил вибираємо три довільні точки А, В, С і складаємо суми моментів відносно цих точок. Ці суми згідно з рівняннями (1.53) повинні дорівнювати
(рис. 53). В площині дії сил вибираємо три довільні точки А, В, С і складаємо суми моментів відносно цих точок. Ці суми згідно з рівняннями (1.53) повинні дорівнювати
нулеві.

Рис. 53


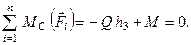
Оскільки в отриманих рівняннях хоча б одне  (інакше точки А, В і С будуть знаходитись на одній лінії, що забороняється умовами (1.53)), то отримаємо
(інакше точки А, В і С будуть знаходитись на одній лінії, що забороняється умовами (1.53)), то отримаємо  а це означає, що головний вектор і головний момент розглянутої системи відповідно дорівнюють нулеві
а це означає, що головний вектор і головний момент розглянутої системи відповідно дорівнюють нулеві  , тобто вона задовольняє необхідній і достатній умові рівноваги.
, тобто вона задовольняє необхідній і достатній умові рівноваги.
Тепер розглянемо частковий випадок плоскої системи сил – плоску систему паралельних сил. Систему координат виберемо так, щоб вісь  була паралельною лініям дій сил (рис. 54). Розглянута система сил буде зрівноважена, коли будуть виконуватись умови (1.51) або (1.52), бо вони є умовами рівноваги будь-якої плоскої системи сил. В даних системах умов перша умова виконується тотожно, тобто
була паралельною лініям дій сил (рис. 54). Розглянута система сил буде зрівноважена, коли будуть виконуватись умови (1.51) або (1.52), бо вони є умовами рівноваги будь-якої плоскої системи сил. В даних системах умов перша умова виконується тотожно, тобто  її можна виключити і тоді отримаємо з умов (1.51)
її можна виключити і тоді отримаємо з умов (1.51)
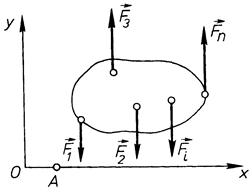
Рис. 54
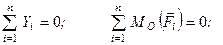 (1.54)
(1.54)
а з умов (1.52)
 (1.55)
(1.55)
Умови (1.54) і (1.55) є аналітичними умовами рівноваги плоскої системи паралельних сил у двох формах:
Перша форма:
Для рівноваги плоскої системи сил необхідно і достатньо, щоб сума проекцій всіх сил системи на вісь, яка паралельна силам, і сума алгебраїчних моментів всіх сил системи відносно довільної точки, що лежить в площині дії сил, дорівнювали нулеві.
Друга форма:
Для рівноваги плоскої системи паралельних сил необхідно і достатньо, щоб суми алгебраїчних моментів всіх сил системи відносно двох будь-яких точок А і В, що лежать в площині дії сил і не лежать на прямій, яка паралельна лініям дії сил, дорівнювали нулеві.
Отже, для довільної плоскої системи сил маємо три умови рівноваги, які записані в трьох формах (1.51)–(1.53). Для плоскої системи паралельних сил маємо дві умови рівноваги в двох формах (1.54)–(1.55). Треба зауважити:
1. Система (1.51) є основною формою умов рівноваги довільної плоскої системи сил. Для плоскої системи паралельних сил основною формою умов рівноваги є система (1.54). Це, по-перше, пояснюється тим, що дані умови рівноваги не накладають обмежень на вибір системи координат і точки, відносно якої складається сума моментів. По-друге, скласти суму проекцій сил на вісь, в основному, є легше, ніж скласти суму моментів цих сил відносно точки.
2. Якщо при розв’язанні задачі використовується одна форма умови рівноваги, то для отримання додаткової інформації не треба брати умови рівноваги з другої форми. Коротше кажучи, для довільної плоскої системи сил, що діє на якесь тіло, можна скласти тільки три рівняння рівноваги. Додатково складене рівняння рівноваги ніякої нової інформації не дасть, бо після відповідних перетворень воно співпаде з одним із попередніх рівнянь.
Статично означені і статично неозначені задачі
Задачі на рівновагу механічних систем, які розв’язу-ються методами статики твердого тіла, називають-ся статично означеними. В протилежному разі задачі статично неозначені.
Механічні системи, яких це стосується, називаються відповідно статично визначеними і статично невизначеними.
Задачі на рівновагу тіл в статиці розв’язуються методом складання незалежних рівнянь рівноваги. Як відомо з попереднього, кожна система сил має свою… Очевидно, задача буде статично означеною, якщо (1.56)Рис. 55

Рис. 56
шарніром В. Оскільки реакція нерухомого циліндричного шарніра має дві складові  а реакція рухомої опори
а реакція рухомої опори  перпендикулярна до опорної поверхні, то в даному варіанті закріплення балки маємо три невідомі:
перпендикулярна до опорної поверхні, то в даному варіанті закріплення балки маємо три невідомі:  На балку діє плоска система сил, для якої можна скласти три незалежних рівняння рівноваги, отже,
На балку діє плоска система сил, для якої можна скласти три незалежних рівняння рівноваги, отже,  тобто задача є статично означеною.
тобто задача є статично означеною.
Якщо балку АВ прикріпити до горизонтальної поверхні двома нерухомими шарнірами (рис. 56, а), то задача буде статично неозначеною, оскільки число невідомих  дорівнює чотирьом
дорівнює чотирьом 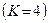 , а для плоскої системи сил, яка діє на балку, можна скласти тільки три незалежних рівняння рівноваги, тобто кількість рівнянь рівноваги, які дає статика, є недостатньою для однозначного визначення всіх реакцій опор. Для розв’язання такої задачі необхідно враховувати пружні властивості тіла АВ, його деформацію, що не входить до компетенції теоретичної механіки. Такі задачі будуть розв’язува-тися в “Опорі матеріалів”.
, а для плоскої системи сил, яка діє на балку, можна скласти тільки три незалежних рівняння рівноваги, тобто кількість рівнянь рівноваги, які дає статика, є недостатньою для однозначного визначення всіх реакцій опор. Для розв’язання такої задачі необхідно враховувати пружні властивості тіла АВ, його деформацію, що не входить до компетенції теоретичної механіки. Такі задачі будуть розв’язува-тися в “Опорі матеріалів”.
Умова статичної означеності задачі (умова 1.56) значно розширюється для систем тіл, що з’єднані між собою і перебувають в рівновазі.
Рівновага системи тіл
Розглянемо рівновагу системи тіл, які з’єднані між собою за допомогою шарнірів, гнучких ланок (наприклад, тросів) або вільно спираються одне на одного.
Сили, які діють на таку систему, можна поділити на зовнішні і внутрішні.
Зовнішніми силами називаються сили, з якими тіла системи взаємодіють з тілами, що не входять в дану систему.
Внутрішні сили – це сили взаємодії між тілами однієї і тієї ж системи.
Якщо нитку CD розрізати і розглянути систему двох вантажів (рис. 57, б), то для даної системи зовнішніми силами будуть: – сили ваги вантажів; –… З наведених прикладів видно, що поділ сил на зовнішні і внутрішні, як було… До того ж з наведеного видно, що внутрішні сили деякої системи тіл можна перевести в зовнішні відносно нової системи,…Рис. 58
 ;
;  ;
;
 ;
;  ;
;
 ;
;  .
.
Підставляючи числові значення, маємо
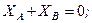


Звідси 
Для знаходження 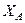 і
і 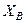 потрібно мати ще рівняння рівноваги. Для отримання цього рівняння розглянемо рівновагу стрижня АС, на який діють (рис. 59)
потрібно мати ще рівняння рівноваги. Для отримання цього рівняння розглянемо рівновагу стрижня АС, на який діють (рис. 59)  – задані сили;
– задані сили;  – реакції в’язей.
– реакції в’язей.
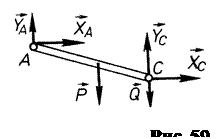 Діюча система сил є плоскою і можна скласти три рівняння рівноваги. Нам для розв’язання задачі потрібно тільки одне рівняння, а тому складемо суму моментів сил відносно точки С, адже тільки це рівняння не включатиме нові невідомі
Діюча система сил є плоскою і можна скласти три рівняння рівноваги. Нам для розв’язання задачі потрібно тільки одне рівняння, а тому складемо суму моментів сил відносно точки С, адже тільки це рівняння не включатиме нові невідомі 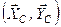

| 


|
Звідси  отже,
отже, 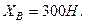
Питання для самоконтролю
1. Яка система сил називається довільною?
2. Що називається головним вектором довільної системи сил?
3. Що називається головним моментом системи сил відносно деякої точки?
4. Як геометрично визначається головний вектор довільної системи сил?
5. Запишіть формули, за допомогою яких аналітично визначається головний вектор довільної системи сил.
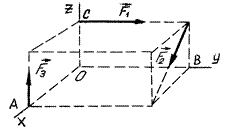 6. Визначіть головний вектор системи сил, яка зображена на рисунку, якщо
6. Визначіть головний вектор системи сил, яка зображена на рисунку, якщо
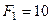 Н,
Н,  Н,
Н,
 Н,
Н, 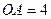 м,
м,
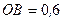 м,
м, 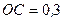 м.
м.
7. Запишіть формули, за допомогою яких аналітично визначається головний момент довільної системи сил відносно деякої точки.
8. Визначіть головний момент системи сил відносно початку координат, яка задана в прикладі № 6.
9. Що називається парою сил?
10. Сформулюйте теорему про момент пари сил відносно довільної точки.
11. Який напрям має вектор моменту пари сил?
12. Запишіть формулу, яка чисельно визначає момент пари сил відносно деякої точки.
13. Які пари сил називається еквівалентними?
14. Сформулюйте теорему про додавання пар сил.
15. До якого канонічного вигляду зводиться система пар сил?
16. Сформулюйте необхідну і достатню умову рівноваги системи пари сил.
17. Запишіть аналітичні умови рівноваги системи пар сил.
18. Сформулюйте лему про паралельний перенос сили в деяку точку.
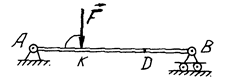 19. Силу
19. Силу 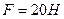 паралельно перенесли з точки К в точку D. Що треба зробити, щоб величини реакцій шарнірів А і В не змінились, якщо
паралельно перенесли з точки К в точку D. Що треба зробити, щоб величини реакцій шарнірів А і В не змінились, якщо  м, KD = 0,4 м ?
м, KD = 0,4 м ?
20. Якщо довільну систему сил звести до деякого центра, що в загальному випадку отримаємо?
21. Коли довільна система сил зводиться до пари сил?
22. В яких випадках канонічним виглядом довільної системи сил є рівнодійна?
23. Що таке динама?
24. Сформулюйте необхідну і достатню умову рівноваги довільної системи сил.
25. Запишіть аналітичні умови рівноваги довільної просторової системи сил.
26. Запишіть аналітичні умови рівноваги довільної плоскої системи сил.
27. В яких формах можна записати аналітичні умови рівноваги довільної плоскої системи сил?
28. Що називається інваріантом довільної системи сил?
29. Які Ви знаєте інваріанти довільної системи сил?
30. Запишіть формулу, яка відображає залежність головного моменту системи сил від центра зведення.
31. Які задачі називаються статично означеними?
32. Як класифікуються сили, що діють на систему тіл, з’єднаних між собою?
33. Задано систему двох тіл, з’єднаних між собою. На одне тіло діє довільна плоска система сил, на інше – плоска система паралельних сил. Скільки найбільше невідомих можна визначити в цій задачі?
Деякі спеціальні питання статики
В попередніх розділах були розв’язані основні задачі теоретичного курсу статики – це зведення систем до канонічного вигляду і визначення умов (рівнянь) їх зрівноваження. Тепер розглянемо деякі питання, котрі, з одного боку, розширюють коло задач, які розв’язує статика в напрямку їх реальності, а, з другого боку, стануть прикладом практичного застосування от-риманих положень для розв’язування конкретних задач. Одним із напрямків реалізації задач статики є врахування сил тертя.
Опір, що виникає при русі або намаганні рухатися одного тіла по поверхні іншого, називається тертям.
Оскільки найчастіше одне тіло може ковзати або котитись по поверхні іншого тіла, то в теоретичній механіці розглядають два види тертя: тертя ковзання і тертя кочення.
Тертя ковзання
Опір, що виникає при ковзанні або намаганні ковзати одного тіла по поверхні іншого, називається тертям ковзання.
Прикладемо до тіла горизонтальну силу (рис. 60, б). Якщо б реакція поверхні визначалась тільки однією силою , то під дією незначного зусилля тіло… З умови рівноваги () маємо ,Рис. 61
Конус тертя. Область рівноваги
Нормальна реакція  і сила тертя в сумі визначають повну реакцію опорної поверхні (рис. 62), тобто реакція шорсткої поверхні дорівнює геометричній сумі вказаних сил
і сила тертя в сумі визначають повну реакцію опорної поверхні (рис. 62), тобто реакція шорсткої поверхні дорівнює геометричній сумі вказаних сил
 . (1.61)
. (1.61)

Рис. 62
Ця реакція відхилена від нормалі до поверхні на деякий кут 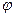 . Із зміною сили тертя від нуля до максимального значення (
. Із зміною сили тертя від нуля до максимального значення ( ) змінюватиметься і реакція
) змінюватиметься і реакція 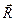 поверхні від
поверхні від  до
до  , а її кут з нормаллю до поверхні збільшуватиметься від нуля до деякого граничного значення
, а її кут з нормаллю до поверхні збільшуватиметься від нуля до деякого граничного значення  (рис. 63).
(рис. 63).

Рис. 63
Найбільший кут jС , на який повна реакція поверхні відхиляється від нормалі до неї, називається кутом тертя.
З рис. 63 видно, що

Враховуючи формулу (1.59), отримаємо
 , (1.62)
, (1.62)
тобто,
Тангенс кута тертя чисельно дорівнює коефіцієнту статичного тертя.
При зміні напряму прикладання активної сили  буде змінюватись напрям сили тертя
буде змінюватись напрям сили тертя  , а реакція
, а реакція  поверхні буде описувати конічну поверхню (рис. 64).
поверхні буде описувати конічну поверхню (рис. 64).
Конус, вершина якого знаходиться в точці дотику тіла з поверхнею, а твірна з нормаллю до поверхні утворює кут тертя, називається конусом тертя.
Якщо коефіцієнт тертя в усіх напрямах однаковий, то конус тертя буде круговим.
Область, обмежена конусом тертя, називається обла-стю рівноваги.

Рис. 64
Така назва пояснюється тим, що коли активні сили, котрі діють на тіло, зводяться до рівнодійної, лінія дії якої знаходиться в області, обмеженій конусом тертя, то якою б великою вона не була, тіло перебуватиме в стані спокою.
 Для доведення цього розглянемо тіло на шорсткій поверхні. Позначимо рівнодійну активних сил, що діють на тіло,
Для доведення цього розглянемо тіло на шорсткій поверхні. Позначимо рівнодійну активних сил, що діють на тіло,  і нехай вона утворює кут
і нехай вона утворює кут 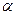 з нормаллю до поверхні (рис. 65).
з нормаллю до поверхні (рис. 65).
Умовою спокою тіла на поверхні є
 , (а)
, (а)
Оскільки 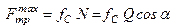 , то умова (а) набуває вигляду
, то умова (а) набуває вигляду
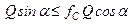 ,
,
або
 .
.
Враховуючи формулу (1.62), отримуємо
 .
.
З отриманої нерівності випливає, що, коли до тіла, що знаходиться на шорсткій поверхні, прикладено силу  , котра утворює з нормаллю до поверхні кут, менший від кута тертя, то тіло буде перебувати в стані спокою. Цим пояснюються такі відомі явища в техніці, як заклинювання або самогальмування.
, котра утворює з нормаллю до поверхні кут, менший від кута тертя, то тіло буде перебувати в стані спокою. Цим пояснюються такі відомі явища в техніці, як заклинювання або самогальмування.
Тертя кочення
Опір, який протидіє коченню одного тіла по поверхні іншого, називається тертям кочення.
, , .Рис. 67
При прикладанні сили  до циліндричного тіла, як вказано на рис. 66, очевидно, тиск тіла на опорну поверхню в зоні АВ (див. рис. 67, а) буде зменшуватись, а в зоні AD – зростати, і інтенсивність реакцій опорної поверхні буде збільшуватись в бік дії сили
до циліндричного тіла, як вказано на рис. 66, очевидно, тиск тіла на опорну поверхню в зоні АВ (див. рис. 67, а) буде зменшуватись, а в зоні AD – зростати, і інтенсивність реакцій опорної поверхні буде збільшуватись в бік дії сили  . Розподіл реакцій опорної поверхні набуває вигляду, як зображено на рис. 67, б. При такому розподілі рівнодійна реакція поверхні
. Розподіл реакцій опорної поверхні набуває вигляду, як зображено на рис. 67, б. При такому розподілі рівнодійна реакція поверхні 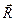 , буде зміщена в бік дії сили
, буде зміщена в бік дії сили  на деяку відстань
на деяку відстань 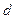 , і в положенні рівноваги розподіл сил, що діють на циліндр, буде мати вигляд, який зображений на рис. 67, б. При такому розподілі сил, що діють на циліндр, по-перше, задовольняється рівняння моментів
, і в положенні рівноваги розподіл сил, що діють на циліндр, буде мати вигляд, який зображений на рис. 67, б. При такому розподілі сил, що діють на циліндр, по-перше, задовольняється рівняння моментів

по-друге, цей розподіл задовольняє теорему про три сили.
При рівновазі котка  і
і  , тобто на коток діють дві пари сил. Пара сил
, тобто на коток діють дві пари сил. Пара сил  намагається котити коток, а пара сил
намагається котити коток, а пара сил 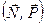 протидіє цьому рухові. Момент пари сил
протидіє цьому рухові. Момент пари сил  називається моментом тертя кочення, і він дорівнює
називається моментом тертя кочення, і він дорівнює 
Величина зміщення 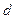 буде збільшуватись із зростанням сили
буде збільшуватись із зростанням сили  . В граничному положенні рівноваги, тобто в момент початку кочення, це зміщення досягне свого максимального значення. Очевидно, це максимальне зміщення буде залежати від фізичних властивостей матеріалів опорної поверхні і циліндричного тіла, тобто є деякою характеристикою цих матеріалів.
. В граничному положенні рівноваги, тобто в момент початку кочення, це зміщення досягне свого максимального значення. Очевидно, це максимальне зміщення буде залежати від фізичних властивостей матеріалів опорної поверхні і циліндричного тіла, тобто є деякою характеристикою цих матеріалів.
Максимальне зміщення нормальної реакції опорної поверхні в бік дії сили при коченні циліндричного тіла називається коефіцієнтом тертя кочення.
. (1.63) Якщо отриману формулу порівняти з формулою (1.60), за допомогою якої… 1. Сталь по сталі 5×10-5 м.Рис. 68
Поняття про ферми
Ферма – це шарнірно-стрижневі геометрично незмінні конструкції.
Деякі варіанти таких конструкцій зображені на рис. 69. Область застосування таких конструкцій надзвичайно різноманітна. За своїм призначенням ферми поділяють на:
1. Мостові ферми (рис. 69, а). Вони використовуються при будівництві мостів.
2. Кроквяні ферми (рис. 69, б), які використовуються як каркаси для підтримування покриття будинків і інших споруд.
3. Кранові ферми (рис. 69, в). Вони використовуються в підйомних механізмах.

Рис. 69
Ферми поділяються на плоскі і просторові. Якщо всі стрижні ферми лежать в одній площині, то ферма називається плоскою, якщо не лежить в одній площині, то – просторовою. Нижче зупинимося на розгляді плоских ферм.
Визначення ферми як шарнірно стрижневої конструкції є ідеалізованим. В реальних фермах стрижні з’єднані жорстко за допомогою заклепок або електрозварювання. До того ж, в теоретичній механіці на ферми накладають і інші умови, які спрощують їх розрахунок. Такими умовами є:
1. Всі стрижні ферми – прямолінійні.
2. Вагою стрижнів нехтується.
3. Шарніри розміщені тільки на кінцях стрижнів.
4. Самі шарніри, що з’єднують стрижні, є ідеальними, тобто тертям в них нехтується.
5. При розгляді плоских ферм всі сили, що діють на ферму, розміщені в площині ферми і прикладені тільки до її вузлів (шарнірів).
При виконанні даних умов кожний стрижень ферми буде зазнавати зусиль, котрі діють вздовж його осі, тобто стрижні ферми будуть працювати тільки на розтяг або на стиск.
З-поміж всього класу ферм виділимо ферми без зайвих стрижнів.
Якщо конструкція ферми така, що з неї не можна зняти ні одного стрижня, не позбавивши її геометрич-но незмінної конструкції, то така ферми називається фермою без зайвих стрижнів.
 Встановимо залежність між кількістю стрижнів
Встановимо залежність між кількістю стрижнів 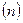 і числом вузлів
і числом вузлів  плоскої ферми без зайвих стрижнів. Найпростішою геометрично незмінною шарнірно стрижневою конструкцією є трикутник, який складається з трьох стрижнів, що з’єднані між собою шарнірами А, В, С (рис. 70). Для утворення кожного наступного вузла (наприклад, вузла D) необхідно два стрижні. Отже, для утворення
плоскої ферми без зайвих стрижнів. Найпростішою геометрично незмінною шарнірно стрижневою конструкцією є трикутник, який складається з трьох стрижнів, що з’єднані між собою шарнірами А, В, С (рис. 70). Для утворення кожного наступного вузла (наприклад, вузла D) необхідно два стрижні. Отже, для утворення  вузлів треба
вузлів треба 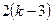 стрижнів. Загальна кількість стрижнів
стрижнів. Загальна кількість стрижнів 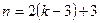 . Звідки отримуємо залежність між кількістю стрижнів і числом вузлів для ферми без зайвих стрижнів
. Звідки отримуємо залежність між кількістю стрижнів і числом вузлів для ферми без зайвих стрижнів
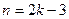 . (1.65)
. (1.65)
Залежність (1.65) є необхідною умовою жорсткості форми, але не достатньою. Для жорсткості ферми без зайвих стрижнів умова (1.65) повинна виконуватися не лише для всієї ферми, але й для кожної гратки ферми.
Для ферм (рис. 71, а і б)  ,
,  і умова (1.65) (
і умова (1.65) (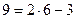 ) виконується, однак ферма (рис. 71, б) є геометрично змінною. Треба зазначити, що (1.65) є одночасно умовою статичної визначеності ферми.
) виконується, однак ферма (рис. 71, б) є геометрично змінною. Треба зазначити, що (1.65) є одночасно умовою статичної визначеності ферми.

Рис. 71
Статично визначеною називається ферма, котру можна розрахувати методами статики твердого тіла.
Розрахувати ферму в статиці означає розв’язати дві задачі:
1. Визначити реакції опор ферми.
2. Визначити зусилля в усіх стрижнях ферми.
При розв’язуванні першої задачі розглядають ферму як тверде тіло, що перебуває в рівновазі під дією навантажень, які діють на неї, та реакцій опор.
Розв’язування другої задачі базується на положенні: якщо якась конструкція, в нашому випадку ферма, перебуває в рівновазі, то кожний її елемент (стрижень, вузол, частина ферми) також знаходиться в рівновазі. Це дає змогу задачу на визначення зусиль в стрижнях ферми розв’язувати двома способами: способом вирізання вузлів і способом перерізів ферми (спосіб Ріттера).
Спосіб вирізання вузлів
Розглянувши рівновагу -вузлів, отримаємо рівнянь рівноваги (або побудуємо замкнутих силових багатокутників), з яких можна отримати невідомих.…Спосіб Ріттера
Якщо два стрижні з трьох розрізаних паралельні, то відповідна точка Ріттера знаходиться в нескінченності. Тоді вибирають умови рівноваги (1.52),…Зауваження
1. При розрахунку вважають, що розрізані стрижні (на рис. 72 – це стрижні 6, 7, 8) працюють на розтяг, тобто зусилля у цих стрижнях – розтягуючі і зображуються  , як вказано на рис. 72. Якщо в дійсності який-небудь стрижень стиснутий, то в результаті розрахунку отримаємо від’ємне число для зусилля в ньому.
, як вказано на рис. 72. Якщо в дійсності який-небудь стрижень стиснутий, то в результаті розрахунку отримаємо від’ємне число для зусилля в ньому.
2. Оскільки розрахунок зусиль в стрижнях ферми в даному способі проводиться за допомогою рівнянь рівноваги плоскої системи сил (а їх є тільки три), то ферму перерізають на дві частини таким чином, щоб в перерізі було не більше трьох стрижнів, зусилля в яких невідомі.

Рис. 72
Питання для самоконтролю
1. Що називається тертям?
2. Що називається тертям ковзання?
3. Що називається тертям кочення?
4. Запишіть формулу, за допомогою якої обчислюється сила тертя ковзання.
5. Що називається кутом тертя?
6. Чому дорівнює тангенс кута тертя?
7. Що таке область рівноваги? Чому вона так називається?
8. Запишіть формулу, за допомогою якої визначається момент тертя кочення.
9. В яких одиницях вимірюються коефіцієнт тертя ковзання і коефіцієнт тертя кочення?
10. Запишіть умову чистого кочення циліндричного тіла по поверхні.
11. Що називається фермою?
12. Як класифікують ферми?
13. Які ферми називаються фермами без зайвих стрижнів?
14. Які ферми називаються статично визначеними?
Система паралельних сил. Центр ваги твердого тіла
Зведення системи паралельних сил до канонічного вигляду
Розглянемо систему  паралельних сил (рис. 73). Для наочності припустимо, що сили вертикальні, а систему координат виберемо так, що вісь Oz буде паралельна силам. Зведемо задані сили до центра О. Для цього визначимо головний вектор і головний момент відносно точки О заданої системи сил. В нашому випадку маємо
паралельних сил (рис. 73). Для наочності припустимо, що сили вертикальні, а систему координат виберемо так, що вісь Oz буде паралельна силам. Зведемо задані сили до центра О. Для цього визначимо головний вектор і головний момент відносно точки О заданої системи сил. В нашому випадку маємо


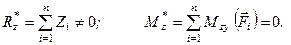

Рис. 73
З отриманих результатів видно, що в загальному випадку головний вектор і головний момент відносно точки О не дорівнюють нулеві. До того ж головний вектор розглянутої системи сил напрямлений по осі Oz (на рис. 73 головний вектор  зображений в припущенні, що
зображений в припущенні, що  ), а головний момент відносно точки О заданої системи сил знаходиться в площині
), а головний момент відносно точки О заданої системи сил знаходиться в площині  (на рис. 73 вектор
(на рис. 73 вектор  зображений в припущенні, що
зображений в припущенні, що  ). Отже, головний вектор і головний момент відносно точки О взаємно перпендикулярні
). Отже, головний вектор і головний момент відносно точки О взаємно перпендикулярні  .
.
Із загальної теорії зведення довільної системи сил до канонічного вигляду відомо, що в даному випадку система сил може бути зрівноваженою (коли  ), звестись до пари сил (коли
), звестись до пари сил (коли  ), або — до рівнодійної (коли
), або — до рівнодійної (коли  або коли
або коли  і
і  ). Отже, в найбільш загальному випадку система паралельних сил зводиться до рівнодійної.
). Отже, в найбільш загальному випадку система паралельних сил зводиться до рівнодійної.
Для випадку, показаному на рис. 73, рівнодійна 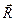 паралельна заданій системі сил, лежить в площині перпендикулярній до головного моменту
паралельна заданій системі сил, лежить в площині перпендикулярній до головного моменту  і пройде через точку
і пройде через точку 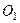 , положення якої знаходиться за формулою (1.45).
, положення якої знаходиться за формулою (1.45).
Властивість системи паралельних сил характеризується такою теоремою:
При повороті системи паралельних сил навколо їх точок прикладання в один і той самий бік і на один і той самий кут рівнодійна буде повертатися на той самий кут навколо фіксованої точки С, яка називається центром паралельних сил.
Доведення. Нехай система паралельних сил  має рівнодійну
має рівнодійну 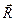 , відмінну від нуля, і нехай точка С є довільною точкою лінії дії цієї рівнодійної (рис. 74.)
, відмінну від нуля, і нехай точка С є довільною точкою лінії дії цієї рівнодійної (рис. 74.)

Рис. 74
Нехай: 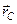 – радіус-вектор точки С;
– радіус-вектор точки С;  – радіус-вектор точки прикладання довільної
– радіус-вектор точки прикладання довільної 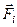 сили системи;
сили системи; 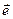 – одиничний вектор напряму дії сил системи. Тоді
– одиничний вектор напряму дії сил системи. Тоді
 (а)
(а)
За теоремою Варіньйона маємо
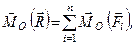
або
 (б)
(б)
 Оскільки
Оскільки  і враховуючи (а), отримаємо
і враховуючи (а), отримаємо
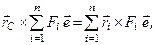
або

Коли перенесемо всі члени цієї рівності в один бік і винесемо за дужку вектор  , отримаємо
, отримаємо
 (в)
(в)
Вимагається, щоб рівність (в) була справедлива для будь-якої орієнтації системи паралельних сил, тобто для будь-якого напряму одиничного вектора 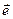 . Це можливо, коли
. Це можливо, коли
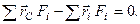 (г)
(г)
Рівність (г) має єдиний розв’язок відносно радіуса-век-тора  , який визначає таку точку прикладання рівнодійної, яка не змінює свого положення при повороті ліній дії сил. Такою точкою і є центр паралельних сил, що і доводить його існування.
, який визначає таку точку прикладання рівнодійної, яка не змінює свого положення при повороті ліній дії сил. Такою точкою і є центр паралельних сил, що і доводить його існування.
Знайдемо радіус-вектор і координати центра паралельних сил. Із (г) маємо
 (1.66)
(1.66)
Отримана формула визначає радіус-вектор центра паралельних сил. Спроектувавши обидві частини векторної рівності на координатні осі, отримаємо
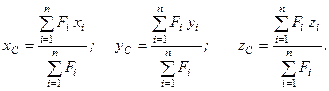 (1.67)
(1.67)
Формули (1.67) визначають координати центра паралельних сил.
Центр ваги твердого тіла
На всі частинки тіла, що знаходяться поблизу поверхні Землі, діє сила ваги, яка є геометричною сумою сили всесвітнього тяжіння і відцентрової сили інерції, зумовленої обертанням Землі навколо своє осі. Оскільки відцентрова сила інерції мала порівняно із силою тяжіння, то практично вважають, що сила ваги напрямлена до центра Землі. Якщо тіло розбити на елементарні частини, сили ваг яких 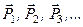 (рис. 75) і врахувати, що розміри тіла є незначними порівняно з розмірами Землі, то сили ваг їх елементарних частин тіла з достатньо великою точністю утворюють систему паралельних сил.
(рис. 75) і врахувати, що розміри тіла є незначними порівняно з розмірами Землі, то сили ваг їх елементарних частин тіла з достатньо великою точністю утворюють систему паралельних сил.
Рівнодійна сил ваг окремих частин тіла називається силою ваги тіла
 . (а)
. (а)
Враховуючи, що сили ваг елементарних частин тіла  паралельні і напрямлені в один бік, векторну рівність (а) можна записати у вигляді
паралельні і напрямлені в один бік, векторну рівність (а) можна записати у вигляді
 (1.68)
(1.68)
тобто
Вага тіла дорівнює сумі ваг окремих його частин.
Центр паралельних сил ваг окремих частин тіла називається центром ваги тіла.

Рис. 75
На рис. 75 центр ваги тіла позначено буквою С. Координати точки С можна обчислити за формулами (1.67), які визначають координати центра паралельних сил, замінивши  на
на 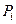
 (1.69)
(1.69)
Записані вирази – це найбільш загальні формули, які визначають координати центра ваги тіла. В даних формулах:
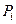 – вага окремої частини тіла;
– вага окремої частини тіла; 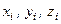 – координати цієї частинки.
– координати цієї частинки.
Сумування в цих формулах проводиться по всіх частинках тіла. Для тіл, вага яких розподілена неперервно по об’єму, сумування замінюють інтегруванням, і формули (1.69) набувають вигляду
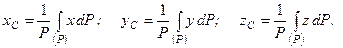 (1.70)
(1.70)
Розглянемо деякі часткові випадки.
1. Центр ваги однорідного тіла (центр ваги об’єму)
До однорідних тіл віднесемо тіла, питома вага яких  по об’єму є сталою, тобто
по об’єму є сталою, тобто  . Тоді
. Тоді  Тут
Тут 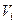 – об’єм частинки тіла.
– об’єм частинки тіла. 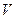 – об’єм всього тіла. Підставивши ці значення в формули (1.69), отримаємо формули, які визначають координати центра ваги однорідного тіла
– об’єм всього тіла. Підставивши ці значення в формули (1.69), отримаємо формули, які визначають координати центра ваги однорідного тіла
 (1.71)
(1.71)
Центр ваги однорідного тіла є центром ваги його об’єму.
2. Центр ваги площі однорідного плоского тіла
(центр ваги площі)
Нехай однорідне плоске тіло буде розміщене в площині 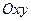 (рис. 76). Його вага і вага окремої його частини визначаються за формулами
(рис. 76). Його вага і вага окремої його частини визначаються за формулами
 (б)
(б)
де:  – вага одиниці площі тіла;
– вага одиниці площі тіла; 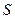 – площа тіла;
– площа тіла;  – площа елементарної його частини. Підставивши (б) в формули (1.69), отримаємо формули, які визначають координати центра ваги однорідного плоского тіла
– площа елементарної його частини. Підставивши (б) в формули (1.69), отримаємо формули, які визначають координати центра ваги однорідного плоского тіла
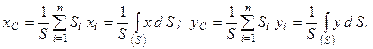 (1.72)
(1.72)
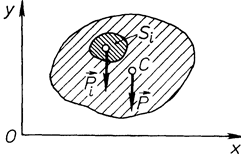
Рис. 76
Під центром ваги площі (плоскої фігури) розуміють центр ваги тонкої однорідної пластини, основа якої співпадає з даною площею. Координати центра ваги площі визначаються за формулами (1.72).
Зазначимо, що:
Сума добутків площі кожного елемента плоскої фігури на його відстань до деякої осі, яка лежить у площині фігури, називається статичним моментом плоскої фігури відносно цієї осі.
Згідно з цим суми  і
і  є статичні моменти нашої плоскої фігури відносно осей
є статичні моменти нашої плоскої фігури відносно осей  і
і 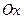 . Позначаючи ці статичні моменти буквами
. Позначаючи ці статичні моменти буквами  і
і 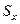 , тобто
, тобто
 (1.73)
(1.73)
отримуємо для координат центра ваги плоскої фігури такі формули:
 (1.74)
(1.74)
За цими формулами вираховують координати центра ваги плоскої фігури, якщо відомі її статичні моменти 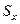 і
і 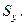
3. Центр ваги однорідного лінійного тіла
(центр ваги лінії)
Позначимо  – вагу одиниці довжини однорідного лінійного тіла. Тоді його вага і вага його елементарної частини визначається за формулами
– вагу одиниці довжини однорідного лінійного тіла. Тоді його вага і вага його елементарної частини визначається за формулами
 (в)
(в)
де:  – довжина тіла;
– довжина тіла;  – довжина
– довжина 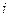 -ого елемента. Підставляючи (в) у формули 1.69), отримаємо формули, які визначають координати центра ваги лінійного однорідного тіла (наприклад, дроту, стрижневої конструкції і т.ін.)
-ого елемента. Підставляючи (в) у формули 1.69), отримаємо формули, які визначають координати центра ваги лінійного однорідного тіла (наприклад, дроту, стрижневої конструкції і т.ін.)
 (1.75)
(1.75)
Під центром ваги лінії розуміють центр ваги тонкого однорідного тіла (стрижня), середня лінія якого співпадає з даною лінією. Координати центра ваги лінії визначаються за формулами (1.75).
Центр ваги деяких простих геометричних фігур
Визначимо центри ваги деяких найпростіших геометричних фігур, які часто зустрічаються в практиці і за допомогою яких можна побудувати більш складні фігури.
Але з самого початку доведемо таку теорему:
Якщо тіло має елемент симетрії (площину, вісь, центр симетрії), то центр ваги тіла знаходиться на цьому елементі симетрії.
(г) оскільки в сумі всі члени попарно знищуються. Отриманий результат, тобто…Рис. 77
Аналогічно можна довести, що центр ваги тіла знаходиться на осі симетрії або в центрі симетрії тіла, якщо воно має відповідні елементи симетрії. Доведення цього положення може базуватись на тому, що вісь симетрії – це лінія перетину двох площин симетрії, а центр симетрії – це точка перетину трьох площин симетрії. Якщо центр ваги тіла одночасно знаходиться в двох (трьох) площинах симетрії, то, очевидно, він знаходиться на лінії (точці) перетину цих площин симетрії.
А тепер розглянемо деякі прості геометричні фігури.
Центр ваги площі паралелограма
З курсу математики середньої школи відомо, що точка перетину діагоналей паралелограма є центром його симетрії. Отже, центр ваги паралелограма (прямокутника, ромба) знаходиться в точці перетину його діагоналей.
Центр ваги площі трикутника
 Для знаходження центра ваги площі трикутника ABD (рис. 78) розіб’ємо його площу на безліч смужок безконечно малої ширини паралельно до сторони AD. Центр ваги кожної такої смужки буде знаходитись в її центрі, тобто на прямій, що з’єднує вер-шину В трикутника з сере-диною протилежної сторо-ни, а це є медіана ВК трикутника. Звідси робимо висновок, що й центр ваги площі всього трикутника лежить на цій медіані.
Для знаходження центра ваги площі трикутника ABD (рис. 78) розіб’ємо його площу на безліч смужок безконечно малої ширини паралельно до сторони AD. Центр ваги кожної такої смужки буде знаходитись в її центрі, тобто на прямій, що з’єднує вер-шину В трикутника з сере-диною протилежної сторо-ни, а це є медіана ВК трикутника. Звідси робимо висновок, що й центр ваги площі всього трикутника лежить на цій медіані.
Розбиваючи трикутник на елементарні смужки лініями, що паралельні стороні АВ (рис. 78), отримаємо, що центр ваги площі трикутника буде знаходитись на медіані DM.
Отже,
Центр ваги площі трикутника знаходиться в точці перетину його медіан.
В аналітичній геометрії доводиться, що координати точки перетину медіан трикутника визначаються за формулами
 (1.76)
(1.76)
Формули (1.76) визначають координати центра ваги трикутника. В цих формулах 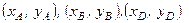 – координати вершин трикутника.
– координати вершин трикутника.
Центр ваги дуги кола
в якій сумування замінимо інтегруванням, тобто (а)Центр ваги площі кругового сектора
(1.79) Отримана формула визначає центр ваги площі сектора круга радіуса . В цій… (1.80)Способи визначення положення центра ваги тіла
Центр ваги твердого тіла можна визначити як експериментально, так і аналітично, тобто проведенням відповідних розрахунків.
Найпростішим експериментальним способом визначення положення центра ваги тіла є:
Спосіб підвішування
Цей спосіб полягає в тому, що тіло послідовно підвішують за дві які-небудь його точки (рис. 81). Оскільки на підвішене тіло діють тільки дві сили (натяг нитки і сила ваги тіла), то в положенні рівноваги ці сили діють по одній прямій в протилежні боки. Отже, центр ваги тіла буде знаходитись на лінії, що є продовженням нитки: якщо тіло підвішено за точку А – то на лінії АА1 (рис. 81, а), якщо за точку В – то на лінії ВВ1 (рис. 81, б). Точка С перетину цих ліній буде центром ваги тіла.

Рис. 81
Спосіб зважування
Для визначення положення центра ваги деякого тіла в точках А, В і D кладемо його на платформи трьох ваг (рис. 82). Тіло перебуває в рівновазі під дією чотирьох сил: 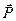 – сила ваги тіла;
– сила ваги тіла;  – реакції платформ, величини яких вкажуть відповідні ваги. Ці сили утворюють систему паралельних сил. Складемо рівняння рівноваги
– реакції платформ, величини яких вкажуть відповідні ваги. Ці сили утворюють систему паралельних сил. Складемо рівняння рівноваги

Рис. 82

 ;
;

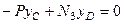 ;
;

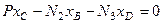 .
.
З першого рівняння знаходимо вагу тіла
 .
.
З другого рівняння визначаємо ординату центра ваги

З третього рівняння знаходимо абсцису центра ваги

Координати  легко визначаються експериментально.
легко визначаються експериментально.
Координату  об’ємного тіла визначимо, якщо тіло повернемо на кут 90° навколо горизонтальної осі і зробимо повторне зважування.
об’ємного тіла визначимо, якщо тіло повернемо на кут 90° навколо горизонтальної осі і зробимо повторне зважування.
Серед аналітичних методів визначення положення центра ваги виділимо:
Спосіб розбиття
Рис. 83
Спосіб від’ємних ваг (площ)
Цей спосіб застосовується для знаходження координат центра ваги тіл, які мають вирізи (пустоти). Розглянемо плоске тіло, що має дві пустоти (рис. 83, б). Позначимо  – вагу тіла, яке має пустоти,
– вагу тіла, яке має пустоти, 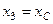 ,
,  – координати його центра ваги;
– координати його центра ваги; 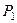 і
і 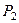 – ваги речовин, які вибрані з пустот 1 і 2;
– ваги речовин, які вибрані з пустот 1 і 2; 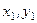 ;
;  – координати центрів ваг пустот;
– координати центрів ваг пустот; 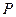 – вага тіла разом з вагою пустот, тобто
– вага тіла разом з вагою пустот, тобто  ;
;  – координати центра ваги тіла, яке не має пустот. Ці координати, очевидно, можна визначити за формулами
– координати центра ваги тіла, яке не має пустот. Ці координати, очевидно, можна визначити за формулами
 (а)
(а)
Оскільки  , а
, а 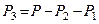 , то з формули (а) знаходимо координати центра ваги тіла, що має пустоти
, то з формули (а) знаходимо координати центра ваги тіла, що має пустоти
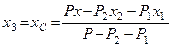 ,
,
 .
.
З отриманих формул можна зробити такий висновок:
Для визначення координат центра ваги тіла, що має вирізи (пустоти), можна використати метод розбиття на такі частини: все тіло разом з пустота-ми та пустоти, але вважати, що пустоти мають від’ємну вагу (для плоского тіла – від’ємну площу).
Питання для самоконтролю
1. Яка система сил називається паралельною?
2. До якого канонічного вигляду можна звести систему паралельних сил?
3. Що називається центром паралельних сил?
4. За якими формулами визначаються координати центра паралельних сил?
5. Що називається вагою тіла?
6. Запишіть найбільш загальні формули, які визначають координати центра ваги тіла.
7. За якими формулами визначаються координати центра ваги однорідного тіла?
8. Запишіть формули, які визначають координати центра ваги однорідного плоского тіла.
9. Запишіть формули, які визначають статичні моменти плоскої фігури відносно осей абсцис і ординат.
10. Тіло має елемент симетрії. Де знаходиться його центр ваги?
11. Де знаходиться центр ваги площі трикутника? За якими формулами можна вирахувати координати центра ваги трикутника?
12. За якою формулою обчислюється координата центра ваги дуги кола?
13. За якою формулою обчислюється координата центра ваги площі кругового сектора?
14. Які є експериментальні способи визначення положення центра ваги тіла? Поясніть їх сутність.
15. Які є аналітичні методи визначення координат центра ваги тіла? Поясніть їх сутність.
КІНЕМАТИКА
Предмет кінематики
Кінематика – це розділ теоретичної механіки, в якому вивчається механічний рух матеріальних об’єктів незалежно від сил, які викликають або змінюють цей рух.
Іншими словами, в кінематиці вивчається переміщення матеріальних об’єктів в просторі і в часі без врахування їх матеріальної структури і взаємодії їх з іншими матеріальними системами. А тому матеріальну точку в кінематиці просто називають точкою, а саму кінематику називають геометрією руху.
Основними завданнями теоретичного курсу кінематики є отримання формул (рівнянь), які визначають кінематичні характеристики механічного руху матеріальних об’єктів. Основними кінематичними характеристиками руху твердого тіла є закон руху, кутова швидкість, кутове пришвидшення, швидкість і пришвидшення точки, яку вибирають за полюс, і т. ін. Кінематичними характеристиками руху точки є закон (рівняння) руху, траєкторія руху, швидкість і пришвидшення точки.
1. Рівняння (закон руху) – математичні рівняння, за допомогою яких можна визначити положення матеріального об’єкта в будь-який момент часу.
2. Траєкторія – це геометричне місце послідовних положень точки в просторі.
З визначення випливає, що поняття траєкторії існує тільки для точки, і тому дана кінематична характеристика визначається або задається тільки в тому випадку, коли вивчається рух точки.
3. Швидкість точки – векторна величина, що характеризує в кожний момент часу бистроту і напрям зміни руху точки в заданій системі відліку.
4. Пришвидшення точки – векторна величина, що характеризує в кожний момент часу бистроту зміни вектора швидкості за величиною і напрямом в заданій системі відліку.
5. Кутова швидкість – в загальному випадку векторна величина, яка характеризує в кожний момент часу бистроту і напрям зміни обертання тіла в заданій системі відліку.
6. Кутове пришвидшення – в загальному випадку векторна величина, яка характеризує в кожний момент часу бистроту і напрям зміни вектора кутової швидкості тіла в заданій системі відліку.
Якщо для певного руху матеріального об’єкта отримані формули, за допомогою яких визначені перераховані кінематичні характеристики, то можна вважати, що основне завдання теоретичного курсу кінематики розв’язане.
Основним завданням практичної частини курсу кінематики є визначення за допомогою формул, отриманих в теоретичному курсі, кінематичних характеристик руху окремих точок матеріального об’єкта. Треба зазначити, що визначені кінематичні характеристики руху, як і сам механічний рух, є відносними. Їх величина і характер зміни залежать від вибору системи відліку. Так, наприклад, траєкторія руху будь-якої точки обода колеса автомобіля, який рухається по дорозі відносно автомобіля, буде коло, а відносно дороги (землі) – циклоїда. А тому при визначенні кінематичних характеристик руху необхідно чітко з’ясувати, в якій системі відліку вони визначаються. В кінематиці систему відліку найчастіше пов’язу-ють з Землею, а останню вважають нерухомою.
Кінематику можна назвати геометричним вченням про рух, бо вона питання про сили, які зумовлюють цей рух, зовсім не розглядає. Ширша постановка питання про рух тіл, де на перший план висувається зв’язок між рухом тіла і прикладеними до нього силами, належить динаміці, а тому кінематику часто трактують як вступ до динаміки. Але треба мати на увазі, що результати встановлені в кінематиці, мають і велике самостійне значення. Для багатьох механізмів питання про діючі сили має порівняно другорядне значення. Правильна ж дія механізму забезпечується досконалим кінематичним аналізом рухів окремих його частин (ланок).
Основними матеріальними об’єктами, механічний рух яких вивчається в кінематиці, є точка і тверде тіло. А тому саму кінематику можна розділити на кінематику точки і кінематику твердого тіла.
Кінематика точки
Рух точки як об’єкта, розмірами якого нехтують, можна розглядати як простий або складний. Простий рух і відносний у випадку складного руху точки можна задати і вивчити трьома способами: векторним, координатним і натуральним.
Векторний спосіб вивчення руху точки
(2.1) Рівняння (2.1) є рівнянням (законом) руху точки у векторній формі. Для…Лінія, яка описується в просторі кінцем змінного вектора, початок якого знаходиться в нерухомій точці, називається годографом даного вектора.
Для визначення швидкості точки розглянемо два її послідовні положення. Припустимо, що в момент часу рухома точка перебуває в положенні , яке… Отже, за проміжок часу точка змістилася на вектор . Відношення приросту… .Швидкість точки дорівнює першій похідній за часом від її радіуса-вектора.
З отриманої формули видно: 1) швидкість точки – це вектор, про що було сказано вище; 2) вектор швидкості точки напрямлений по дотичній до її траєкторії в бік її руху, бо граничне положення вектора , коли…Пришвидшення точки дорівнює першій похідній за часом від вектора її швидкості.
Якщо врахувати формулу (2.2) для швидкості, то отримаємо
 (2.3)
(2.3)
Пришвидшення точки дорівнює другій похідній за часом від її радіуса-вектора.
З отриманих формул випливає:
1. Пришвидшення точки – це вектор.
 2. Вектор пришвидшення точки напрямлений в бік вгнутості її траєкторії і лежить в стичній площині (рис. 86).
2. Вектор пришвидшення точки напрямлений в бік вгнутості її траєкторії і лежить в стичній площині (рис. 86).
3. Вектор пришвидшення точки напрямлений по дотичній до годографа вектора її швидкості. І дійсно, якщо побудувати годограф вектора швидкості (рис. 87), то вектор  – це хорда
– це хорда  , граничне положення якої, коли
, граничне положення якої, коли 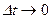 , є дотична.
, є дотична.
Координатний спосіб вивчення руху точки
(2.5) Рішення (2.5) називаються кінематичними рівняннями руху точок в декартовій… Легко встановити зв’язок між векторним і координатним способами задання руху точки. З рис. 88 видно, щоПроекції вектора швидкості на декартові осі координат дорівнюють першим похідним за часом від відповідних координат.
(2.9) і його напрямні косинуси (2.10)Проекції вектора пришвидшення на декартові осі координат дорівнюють другим похідним за часом від відповідних координат.
Знаючи проекції, за формулою
 (2.12)
(2.12)
вираховуємо величину вектора пришвидшення, а його напрямні косинуси – за формулами

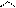
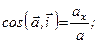

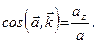 (2.13)
(2.13)
Формули (2.11)-(2.13) визначають вектор пришвидшення точки у випадку, коли рух її задано в декартовій системі координат, тобто задано рівняннями (2.5).
Швидкість і пришвидшення точки в полярних координатах
(2.14) Записані рівняння є рівняннями руху точки в полярних координатах. З рис. 89… (а)Натуральна система координат
Проведемо в цих точках дотичні до кривої, орти яких позначимо відповідно і . Перенесемо вектор паралельно самому собі в точку і через вектори і… Ліня перетину стичної і нормальної площин називається головною нормаллю…Рис. 91
Таким чином, в кожній точці кривої можна провести три взаємно перпендикулярні напрями і прийняти їх за координатні осі: дотичну, напрямлену в бік зростання дугової координати; головну нормаль, напрямлену в бік вгнутості кривої, і бінормаль, напрямлену перпендикулярно до дотичної і головної нормалі так, щоб утворити з ними праву систему осей (рис. 91, а). Якщо поміняти напрям додатного відрахунку на кривій, то поміняють свій напрям дотична вісь і бінормаль (рис. 91, б).
Орти цих осей позначають 
Осі дотична, головна нормаль і бінормаль утворюють натуральну систему координат з початком в рухомій точці, а отже, і рухаються разом з нею, залишаючись взаємно перпендикулярними.
Натуральний спосіб вивчення руху точки
При русі точки її дугова координата неперервно змінюється з часом, тобто є функцією часу (2.17) Записане рівняння, яке дає змогу визначити положення рухомої точки на траєкторії в будь-який момент часу, називається…Рис. 93
Отже, вектор швидкості точки в кожному її положенні є дотичним до траєкторії.
2. Вектор швидкості дорівнює добутку одиничного вектора на вираз  . Згідно з поняттями векторної алгебри цей вираз визначає проекцію вектора швидкості на дотичну вісь і називається алгебраїчноюшвидкістю точки, тобто
. Згідно з поняттями векторної алгебри цей вираз визначає проекцію вектора швидкості на дотичну вісь і називається алгебраїчноюшвидкістю точки, тобто
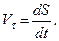 (2.19)
(2.19)
Алгебраїчна швидкість точки дорівнює першій похідній за часом від дугової координати.
Оскільки пришвидшення точки – це перша похідна за ча-сом від її вектора…Пришвидшення точки дорівнює геометричній сумі двох доданків.
(2.21) Скалярний співмножник при орті , очевидно, визначає проекцію нормального… (2.22)Рис. 94
Підставляючи формули (2.21), (2.23) в (2.20), отримаємо
 . (2.25)
. (2.25)
Пришвидшення точки дорівнює геометричній сумі її нормального і тангенціального пришвидшень.
. (2.26) Формули (2.21)-(2.26) визначають вектор пришвидшення точки у випадку, коли рух… З рис. 94 можна зробити такі висновки:Класифікація руху точки за її пришвидшеннями
Найбільш загальною класифікацією руху точки, яка охоплює і згадані класифікації, є класифікація за її пришвидшеннями. Як було показано, в загальному… Розглянемо часткові випадки:Рух з постійним тангенціальним пришвидшенням називається рівнозмінним.
Отже, при рівномірному русі

Інтегруючи  , отримаємо закон зміни алгебра-їчної швидкості при рівнозмінному русі
, отримаємо закон зміни алгебра-їчної швидкості при рівнозмінному русі
 , (2.29)
, (2.29)
в якому  – початкова швидкість точки.
– початкова швидкість точки.
Оскільки  , то формулу (2.29) можна записати
, то формулу (2.29) можна записати

звідки, інтегруючи, отримуємо закон (рівняння) рівнозмінного руху точки
 , (2.30)
, (2.30)
в якому  – початкова дугова координата точки.
– початкова дугова координата точки.
Питання для самоконтролю
1. Що таке “кінематика”?
2. Назвіть основні кінематичні характеристики руху точки.
3. Які рухи може здійснювати точка?
4. Якими способами можна задати рух точки?
5. Запишіть рівняння руху точки у векторній формі.
6. Запишіть рівняння руху точки в декартовій системі координат.
7. Запишіть закон руху точки по траєкторії.
8. Рух точки визначається рівняннями 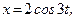
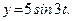 Знайти рівняння траєкторії.
Знайти рівняння траєкторії.
9. Точка рухається по колу радіусом 2 м з постійною швидкістю 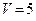 м/с. Яким способом задано рух точки?
м/с. Яким способом задано рух точки?
10. Радіус-вектор точки змінюється за законом 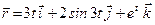 . Запишіть рівняння руху точки в координатній формі.
. Запишіть рівняння руху точки в координатній формі.
11. Рух точки задано рівняннями 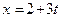 ,
, 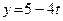 . Знайдіть швидкість точки, якщо
. Знайдіть швидкість точки, якщо  ,
, 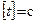 .
.
12. Визначити пришвидшення точки, рух якої описується рівняннями 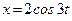 м,
м,  м.
м.
13. Які координати осі називаються натуральними?
14. Як називаються і за якою формулою визначається проекція пришвидшення на головну нормаль?
15. Як називається і за якою формулою визначається проекція пришвидшення на головну нормаль?
16. Чому дорівнює проекція пришвидшення на бінормаль?
17. Як рухається точка, якщо:
а) 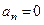 ;
;  ;
;
б)  ;
;  ;
;
в) 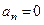 ;
; 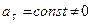 .
.
18. Який рух точки називається рівномірним?
19. Чи може мати пришвидшення точка при рівномірному русі?
20. Запишіть рівняння рівнозмінного руху точки.
Кінематика твердого тіла
При вивченні кінематики як простих, так і складних видів руху твердого тіла розв’язуються дві задачі. З самого початку визначають кінематичні… При русі твердого тіла радіуси-вектори двох його точок в кожний момент часу…Поступальний рух твердого тіла
Поступальним рухом твердого тіла називається такий його рух, при якому будь-яка пряма, що проведена в тілі, залишається паралельною до свого початкового положення.
Найпростішими прикладами поступального руху тіла є:
1. Рух поршня в автомобільному двигуні.
2. Рух стола поздовжньо-стругального верстата.
3. Рух спарника паровозних коліс (рис. 96).
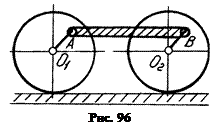 Не треба ототожнювати поступальний рух твердого тіла з прямолінійним рухом. При прямолінійному русі всі точки тіла рухаються по прямій лінії, а при поступальному русі траєкторією точки може бути будь-яка крива.
Не треба ототожнювати поступальний рух твердого тіла з прямолінійним рухом. При прямолінійному русі всі точки тіла рухаються по прямій лінії, а при поступальному русі траєкторією точки може бути будь-яка крива.
 Нехай тіло (рис. 97) здійснює поступальний рух. Візьмемо дві довільні його точки
Нехай тіло (рис. 97) здійснює поступальний рух. Візьмемо дві довільні його точки  і
і  і позначимо:
і позначимо:
 – радіус-вектор точки
– радіус-вектор точки  ;
;
 – радіус-вектор точки
– радіус-вектор точки  ;
;
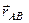 – радіус-вектор точки
– радіус-вектор точки  відносно точки
відносно точки  .
.
Оскільки тіло здійснює поступальний рух  , то вектор
, то вектор  не змінює свого напряму, тобто
не змінює свого напряму, тобто  . Тоді формула (2.31) набуває вигляду
. Тоді формула (2.31) набуває вигляду
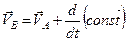 , (а)
, (а)
тобто
 . (б)
. (б)
Отже,
При поступальному русі твердого тіла швидкості його точок геометрично рівні.
Проінтегрувавши векторну рівність (а), отримаємо
 (в)
(в)
З отриманої векторної рівності бачимо, що положення точки  в будь-який момент часу можна отримати шляхом зміщення точки
в будь-який момент часу можна отримати шляхом зміщення точки  на постійний вектор. Отже, траєкторія точки
на постійний вектор. Отже, траєкторія точки  однакова з траєкторією точки
однакова з траєкторією точки  , тільки зміщена на постійний вектор.
, тільки зміщена на постійний вектор.
Диференціюючи рівність (б) за часом, отримаємо
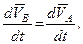
або
 (г)
(г)
тобто:
При поступальному русі твердого тіла пришвидшення його точок геометрично рівні.
Враховуючи отримане, можна сформулювати таку
теорему:
При поступальному русі тіла всі його точки описують однакові траєкторії і в кожний момент часу ма-ють геометрично рівні швидкості і пришвидшення.
А це означає, що поступальний рух твердого тіла визначається рухом окремої його точки.
Ця обставина уможливлює вивчення поступального руху тіла звести до вивчення руху однієї з його точок, тобто до задачі кінематики точки, яка розглянута вище. Наприклад, якщо необхідно записати рівняння поступального руху твердого тіла, то записують рівняння руху якої-небудь його точки
 ,
,  ,
,  . (2.33)
. (2.33)
Рівняння (2.33) за умови, що точка  належить тілу, яке здійснює поступальний рух, називається рівнянням поступального руху твердого тіла. Як буде показано в наступному розділі теоретичної механіки, найефективніше такою точкою вибирати центр мас тіла.
належить тілу, яке здійснює поступальний рух, називається рівнянням поступального руху твердого тіла. Як буде показано в наступному розділі теоретичної механіки, найефективніше такою точкою вибирати центр мас тіла.
Обертання твердого тіла навколо нерухомої осі
Тоді з формули (2.31) отримуємо, що тобтоОбертанням твердого тіла навколо нерухомої осі називається такий його рух, при якому хоча б дві точки тіла є нерухомими.
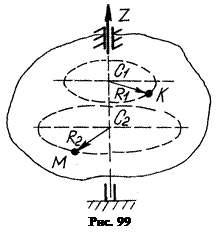 Вісь обертання в подальшому будемо позначати буквою
Вісь обертання в подальшому будемо позначати буквою  Точки тіла, які не належать осі обертання (наприклад, точка
Точки тіла, які не належать осі обертання (наприклад, точка  і
і  (рис. 99), очевидно, рухатимуться по колах, площини яких перпендикулярні до осі обертання, а центри їх знаходяться на осі обертання. Радіуси цих кіл
(рис. 99), очевидно, рухатимуться по колах, площини яких перпендикулярні до осі обертання, а центри їх знаходяться на осі обертання. Радіуси цих кіл  і
і 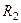 визначають відстані відповідних точок до осі обертання.
визначають відстані відповідних точок до осі обертання.
Рівняння обертання тіла навколо нерухомої осі
(2.34) Записане рівняння називається рівнянням (законом) обертання твердого тіла… Кут поворотувимірюється в радіанах і вважається додатним, якщо він відкладається проти ходу годинникової стрілки, коли…Рівняння рівномірного і рівнозмінного обертання
Обертання з постійною кутовою швидкістю називається рівномірним.
Отже, для рівномірного обертання  Оскільки за формулою (2.35)
Оскільки за формулою (2.35)
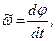
то
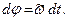
Інтегруючи і враховуючи, що в даному випадку 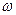 є сталою величною, отримуємо
є сталою величною, отримуємо
 (2.40)
(2.40)
де  – початковий кут повороту. Рівняння (2.40) – це рівняння рівномірного обертання тіла навколо нерухомої осі.
– початковий кут повороту. Рівняння (2.40) – це рівняння рівномірного обертання тіла навколо нерухомої осі.
Обертання з постійним кутовим пришвидшенням називається рівнозмінним.
тобто: .Закон зміни алгебраїчної кутової швидкості при рівнозмінному обертанні
 (2.41)
(2.41)
Закон рівнозмінного обертання тіла навколо нерухомої осі
 (2.42)
(2.42)
У формулах (2.40)-(2.41)  ,
,  , де
, де 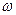 і
і 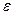 – величини кутової швидкості і кутового пришвидшення.
– величини кутової швидкості і кутового пришвидшення.
Швидкість і пришвидшення точки тіла, яке обертається навколо нерухомої осі
Тут же зображено (див. також рис. 100) – слід нерухомої площини; – слід рухомої площини;Швидкість точки тіла, яке обертається навколо нерухомої осі, за величиною дорівнює добутку кутової швидкості на відстань точки до осі обертання.
Вектор швидкості точки напрямлений по дотичній до траєкторії, в даному випадку до кола, що описується точкою  , в бік обертання. Оскільки дотична до кола перпендикулярна до його радіуса, котрий проведений в точку дотику, то вектор швидкості точки буде перпендикулярним до її радіуса обертання (
, в бік обертання. Оскільки дотична до кола перпендикулярна до його радіуса, котрий проведений в точку дотику, то вектор швидкості точки буде перпендикулярним до її радіуса обертання ( рис. 101). Зауважимо, що швидкість точки тіла, яке обертається, часто називають обертальною швидкістю, а (2.44) – формула, що визначає величину обертальної швидкості.
рис. 101). Зауважимо, що швидкість точки тіла, яке обертається, часто називають обертальною швидкістю, а (2.44) – формула, що визначає величину обертальної швидкості.
За формулами (2.25), (2.22), (2.24), які визначають пришвидшення точки в натуральному способі задання її руху, визначимо пришвидшення точки 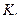
Отже,
Пришвидшення точки тіла, яке обертається нав-коло нерухомої осі, дорівнює геометричній сумі її нормального і тангенціального пришвидшень
 (2.45)
(2.45)
Виразимо складові пришвидшення через кінематичні характеристики обертального руху тіла, тобто через 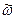 і
і 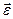 . Маючи на увазі, що радіус кривизни
. Маючи на увазі, що радіус кривизни  траєкторії точки при русі її по колу дорівнює радіусу цього кола, з формули нормального пришвидшення
траєкторії точки при русі її по колу дорівнює радіусу цього кола, з формули нормального пришвидшення  , використовуючи формулу (2.44), отримуємо
, використовуючи формулу (2.44), отримуємо
 ,
,
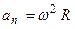 . (2.46)
. (2.46)
Нормальне пришвидшення точки тіла, яке обертається навколо нерухомої осі, дорівнює добутку квадрата кутової швидкості на відстань точки до осі обертання.
З формули  отримаємо
отримаємо
 ,
,
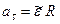 ;
; 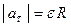 . (2.47)
. (2.47)
Отже,
Алгебраїчне значення тангенціального пришвидшен-ня точки тіла, яке обертається навколо нерухомої осі, дорівнює добутку алгебраїчного кутового пришвидшення на відстань точки до осі обертання.
 Як відомо, вектор нормального пришвидшення точки на-прямлений по головній нормалі до центра кривизни. Головна нормаль кола проходить через його центр. Отже, вектор нормального пришвидшення точки тіла, яке обертається навколо нерухомої осі, напрямлений по радіусу кола до його центра (рис. 102). Вектор тангенціального пришвидшення точки напрямлений по дотичній до траєкторії в бік додатного напряму обертання, якщо
Як відомо, вектор нормального пришвидшення точки на-прямлений по головній нормалі до центра кривизни. Головна нормаль кола проходить через його центр. Отже, вектор нормального пришвидшення точки тіла, яке обертається навколо нерухомої осі, напрямлений по радіусу кола до його центра (рис. 102). Вектор тангенціального пришвидшення точки напрямлений по дотичній до траєкторії в бік додатного напряму обертання, якщо  і в протилежний бік, якщо
і в протилежний бік, якщо  . На рис. 102 вектор
. На рис. 102 вектор 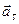 зображений для випадку, коли
зображений для випадку, коли 
Повне пришвидшення визначається діагоналлю прямокутника, побудованого на тангенціальному і нормальному пришвидшеннях. Його величина вираховується за формулою
 . (2.48)
. (2.48)
Напрям вектора повного пришвидшення визначається кутом нахилу  цього вектора до радіуса. Тангенс цього кута (рис. 102)
цього вектора до радіуса. Тангенс цього кута (рис. 102)
 (2.49)
(2.49)
З отриманої формули маємо, що кут нахилу до радіуса кола вектора повного пришвидшення точки тіла, яке обертається навколо нерухомої осі, не залежить від положення точки, яке визначається її радіусом, і для всіх точок він має одне і те ж значення.
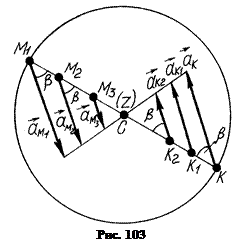 Якщо врахувати, що величина вектора пришвидшення точки тіла, яке обертається навколо нерухомої осі, пропорційна відстані до осі обертання (формула 2.48), а кут нахилу його до відповідного радіуса для всіх точок однаковий, то розподіл (епюр) пришвидшень точок тіла, що обертається навколо нерухомої осі, матиме вигляд, зображений на рис. 103.
Якщо врахувати, що величина вектора пришвидшення точки тіла, яке обертається навколо нерухомої осі, пропорційна відстані до осі обертання (формула 2.48), а кут нахилу його до відповідного радіуса для всіх точок однаковий, то розподіл (епюр) пришвидшень точок тіла, що обертається навколо нерухомої осі, матиме вигляд, зображений на рис. 103.
Формули (2.44)-(2.47) визначають вектор пришвидшення точки тіла, яке обертається навколо нерухомої осі
Примітка. Часто нормальне пришвидшення точок тіла, яке обертається навколо нерухомої осі, називають доцентровим і позначають 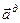 (в російській літературі
(в російській літературі 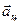 – центро-
– центро-
стремительное ускорение), а тангенціальне пришвидшення називають обертальним пришвидшенням і позначають 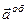 (в російській літературі
(в російській літературі  – вращательное ускорение). При таких позначеннях формула (2.44) набуває вигляду
– вращательное ускорение). При таких позначеннях формула (2.44) набуває вигляду
 (2.49, а)
(2.49, а)
і читається так:
Пришвидшення точок тіла, яке обертається нав-коло нерухомої осі, дорівнює геометричній сумі її доцентрового і обертального пришвидшень.
Вектор кутової швидкості
Вектором кутової швидкості твердого тіла, яке обер-тається навколо нерухомої осі, будемо називати вектор, який чисельно дорівнює модулю алгебраїчної… Вектор є ковзним вектором, бо його можна відкласти з будь-якої точки осі. Задання вектора кутової швидкості повністю визначає обертальний рух тіла, адже він вказує на положення осі обертання,…Перша похідна за часом від вектора кутової швидкості визначає вектор кутового пришвидшення
 (2.51)
(2.51)
або, використовуючи формулу (2.50) і знаючи, що  , матимемо
, матимемо
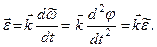 (2.52)
(2.52)
З формули (2.52) випливає, що вектор кутового пришвидшення тіла, що обертається навколо нерухомої осі, також напрямлений по осі обертання, а можливі випадки взаємного розміщення векторів  і
і 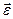 показані на рис. 105).
показані на рис. 105).
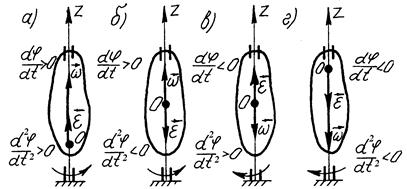
Рис. 105
Векторні вирази швидкості, доцентрового і обертального пришвидшень точки тіла при обертальному русі
– траєкторію довільної точки тіла; – вектор її швидкості , дотичний до траєкторії і напрямлений в бік… – вектор кутової швидкості тіла з довільної її точки в бік, звідки обертання тіла видно проти руху годинникової…Вектор швидкості точки тіла, яке обертається навколо нерухомої осі, дорівнює векторному добутку кутової швидкості на радіус-вектор точки, початок якого знаходиться в довільному центрі на осі.
Формулу (2.53) часто називають формулою Ейлера. Зауважимо, що за часів Л. Ейлера (1707-1783) поняття векторного добутку ще не існувало, але ним були отримані формули
 (2.54)
(2.54)
які є фактично проекціями векторного добутку (2.53) на декартові осі координат.
Оскільки

то враховуючи формулу (2.53), отримаємоформулу, яка визначає значення першої похідної за часом від радіуса-вектора, який змінюється тільки за напрямом
 . (2.55)
. (2.55)
Взявши першу похідну за часом від формули (2.53)

і враховуючи, що 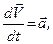

 отримаємо
отримаємо

Легко показати (пропонується кожному читачеві це зробити самостійно), що векторний добуток 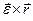 визначає вектор обертального (тангенціального) пришвидшення, а векторний добуток
визначає вектор обертального (тангенціального) пришвидшення, а векторний добуток  визначає вектор доцентрового (нормального) пришвидшення, тобто
визначає вектор доцентрового (нормального) пришвидшення, тобто
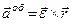 , (2.56)
, (2.56)
 . (2.57)
. (2.57)
Формули (2.53), (2.56), (2.57) є векторними виразами швидкості, тангенціального (обертального) і нормального (до-центрового) пришвидшень.
Питання для самоконтролю
1. Наведіть приклади простих рухів твердого тіла.
2. Який рух твердого тіла називається поступальним?
3. Сформулюйте теорему про траєкторії, швидкості і пришвидшення точок тіла, котре здійснює поступальний рух.
4. Запишіть кінематичні рівняння поступального руху твердого тіла.
5. Який рух твердого тіла називається обертальним нав-коло нерухомої осі?
6. Запишіть рівняння обертання твердого тіла навколо нерухомої осі.
7. Тіло обертається навколо нерухомої осі за законом 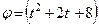 рад. Визначте його кутову швидкість і кутове пришвидшення в момент
рад. Визначте його кутову швидкість і кутове пришвидшення в момент  с.
с.
8. При рівномірному обертанні маховик робить 2 оберти за хвилину. За який час маховик повертається на кут 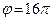 рад?
рад?
9. Ротор електродвигуна робить 900 об/хв. З якою кутовою швидкістю в рад/с обертається ротор?
10. Кутове пришвидшення тіла, яке обертається навколо нерухомої осі, змінюється за законом  с–2. Визначіть кутову швидкість тіла в момент
с–2. Визначіть кутову швидкість тіла в момент  с, якщо в початковий момент часу
с, якщо в початковий момент часу  воно мало кутову швидкість
воно мало кутову швидкість  с–1.
с–1.
11. Тіло обертається навколо нерухомої осі з кутовим пришвидшенням  с–2. Яку кутову швидкість матиме тіло в момент часу
с–2. Яку кутову швидкість матиме тіло в момент часу  с, якщо в початковий момент часу
с, якщо в початковий момент часу  воно мало кутову швидкість
воно мало кутову швидкість  с–1.
с–1.
12. Тіло починає обертатись зі стану спокою з кутовим пришвидшенням  с–2. Скільки обертів зробить тіло за
с–2. Скільки обертів зробить тіло за
4 с?
13. Тіло обертається навколо нерухомої осі за законом  рад. Визначіть швидкість точки тіла, яка знаходиться на відстані 0,35 м від осі обертання.
рад. Визначіть швидкість точки тіла, яка знаходиться на відстані 0,35 м від осі обертання.
14. Швидкість точки тіла, яка знаходиться на відстані  м від осі обертання змінюється за законом
м від осі обертання змінюється за законом  м/с. Визначіть кутове пришвидшення тіла.
м/с. Визначіть кутове пришвидшення тіла.
15. Тіло обертається навколо нерухомої осі за законом  рад. Визначіть нормальне пришвидшення точки тіла, яка знаходиться на відстані 0,4 м від осі обертання, в момент часу
рад. Визначіть нормальне пришвидшення точки тіла, яка знаходиться на відстані 0,4 м від осі обертання, в момент часу  c.
c.
16. Тіло обертається навколо нерухомої осі за законом  рад. Визначіть в момент часу
рад. Визначіть в момент часу 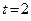 c тангенціальне пришвидшення точки тіла, яка знаходиться на відстані 0,2 м від осі обертання.
c тангенціальне пришвидшення точки тіла, яка знаходиться на відстані 0,2 м від осі обертання.
17. Тіло обертається навколо нерухомої осі за законом  рад. Визначіть в момент часу
рад. Визначіть в момент часу 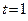 c пришвид-шення точки тіла, яка знаходиться на відстані 0,5 м від осі
c пришвид-шення точки тіла, яка знаходиться на відстані 0,5 м від осі
обертання.
18. Тіло обертається навколо нерухомої осі за законом 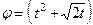 рад. Визначіть кут нахилу до радіуса-вектора пришвидшення точки тіла, яка знаходиться на відстані 0,3 м від осі обертання. Як залежить цей кут від положення точки?
рад. Визначіть кут нахилу до радіуса-вектора пришвидшення точки тіла, яка знаходиться на відстані 0,3 м від осі обертання. Як залежить цей кут від положення точки?
19. Дайте коротку характеристику вектора кутової швидкості.
20 Який напрям має вектор кутового пришвидшення?
Кінематика складного руху точки
Складний рух точки
Складним рухом точки називається такий її рух, при якому точка одночасно рухається відносно двох або більше систем відліку, одна з яких нерухома.
Так, наприклад, переміщення пасажира в рухомому поїзді відносно Землі є складним рухом. По-перше, пасажир рухається з поїздом, по-друге, пасажир переміщується відносно вагона (поїзда). Якщо врахувати рух Землі, то всі тіла, які рухаються по поверхні Землі, здійснюють також складний рух, адже вони рухаються разом з Землею і переміщаються відносно її поверхні. Прикладів складного руху точки можна навести безліч, бо рух кожного тіла (точки), якщо дивитись “в корінь”, є складним.
Вивчення складного руху є важливим не тільки тому, що всі тіла (точки) фактично його здійснюють, а й тому, що розв’язання багатьох задач на кінематичний розрахунок ефективно проводити шляхом розкладання заданого руху на більш прості рухи. До того ж розв’язання великої кількості задач механіки (наприклад, розрахунок траєкторії польоту космічних апаратів; розробка теорії навігаційних приладів і т.п.) потребує врахування руху систем відліку.
Основні поняття і визначення
– нерухому систему координат; – тіло, яке здійснює деякий рух в системі координат ; в подальшому це тіло… – рухому систему координат, яка жорстко зв’язана з носієм;Рис. 107
Рух точки  відносно системи координат
відносно системи координат  є складним. Він складається з руху точки
є складним. Він складається з руху точки  відносно носія і руху, який надається точці носієм.
відносно носія і руху, який надається точці носієм.
Введемо основні поняття і визначення, якими користуються при розгляді складного руху точки.
1. Рух точки К відносно нерухомої системи координат називається абсолютним рухом. Траєкторія, швидкість і пришвидшення точки в абсолютному русі, тобто відносно нерухомої системи координат  , називаються абсолютними.
, називаються абсолютними.
Абсолютну швидкість і абсолютне пришвидшення позначають відповідно  і
і 
Згідно з рис. 107 положення точки  в нерухомій системі координат визначається радіусом-вектором
в нерухомій системі координат визначається радіусом-вектором 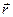 , тоді рівняння
, тоді рівняння

очевидно, описуватиме абсолютний рух точки. Абсолютна швидкість і пришвидшення визначається як відповідні похідні за часом від радіуса-вектор 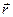 , тобто
, тобто
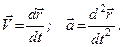 (a)
(a)
2. Рух точки К відносно рухомої системи координат називається відносним рухом. Траєкторія, швидкість і пришвидшення точки у відносному русі, тобто відносно рухомої системи координат  (носія), називаються відносними.
(носія), називаються відносними.
Відносна швидкість і відносне пришвидшення позначаються відповідно 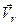 і
і 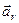 (індекс “
(індекс “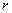 ” від французького слова relatif – відносний).
” від французького слова relatif – відносний).
Положення точки  в рухомій системі координат визначається радіусом-вектором
в рухомій системі координат визначається радіусом-вектором 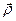 , зміна якого зумовлена двома причинами: відносним рухом точки; переміщенням рухомої системи координат. Щоб виключити останню причину зміни
, зміна якого зумовлена двома причинами: відносним рухом точки; переміщенням рухомої системи координат. Щоб виключити останню причину зміни 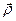 , необхідно рухому систему координат умовно зупинити (“заморозити”). Замороження рухомої системи координат
, необхідно рухому систему координат умовно зупинити (“заморозити”). Замороження рухомої системи координат
математично позначається  . За такої умови
. За такої умови 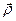 як функція часу буде описувати відносний рух точки, тобто рівняння
як функція часу буде описувати відносний рух точки, тобто рівняння

описує відносний рух точки. Відносна швидкість і пришвидшення визначаються як відповідні похідні за часом від радіуса-вектора 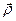
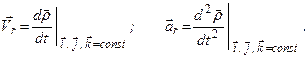 (б)
(б)
3. Рух рухомої системи координат (носія) відносно нерухомої системи координат називається переносним рухом. Швидкість і пришвидшення точки носія, з якою в даний момент співпадає точка  , називається переносними.
, називається переносними.
Переносна швидкість і переносне пришвидшення позначається відповідно 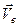 і
і  (індекс “
(індекс “ ” від французького слова entrainer – переносити). В нашому випадку точка
” від французького слова entrainer – переносити). В нашому випадку точка  , яка здійснює складний рух, в даний момент часу співпадає з точкою
, яка здійснює складний рух, в даний момент часу співпадає з точкою  носія (рис. 107), отже швидкість і пришвидшення точки
носія (рис. 107), отже швидкість і пришвидшення точки  для точки
для точки  будуть переносними, тобто:
будуть переносними, тобто:
 (в)
(в)
Як приклад, розглянемо переміщення пасажира в рухомому поїзді. Як було сказано вище, пасажир здійснює складний рух – рухається разом з поїздом і переміщається відносно поїзда (вагона). То згідно зі сформульованими визначеннями рух пасажира відносно поверхні Землі (в даному прикладі Землю вважаємо нерухомою) буде абсолютним рухом. Швидкість і пришвидшення пасажира відносно поверхні Землі є абсолютними. Переміщення пасажира відносно поїзда (вагона) є відносним рухом. Швидкість і пришвидшення пасажира відносно вагона є відносними. Для встановлення відносного руху пасажира і його характеристик необхідно, щоб спостерігач перебував у цьому ж вагоні, а це означає, що носій (в нашому випадку вагон) відносно спостерігача “заморожений”. Рух вагона для пасажира буде переносним рухом. І дійсно, вагон переносить пасажира відносно поверхні Землі. Переносною швидкістю і переносним пришвидшенням для пасажира будуть швидкість і пришвидшення точки вагона, з якою в даний момент співпадає пасажир. Враховуючи, що вагон здійснює поступальний рух, швидкість і пришвидшення вагона для пасажира будуть переносними.
Основним завданням теоретичного курсу кінематики складного руху точки є встановлення залежності між кінематичними характеристиками абсолютного, переносного і відносного рухів.
Теорема про складання швидкостей
(г) Оскільки –координати точок в рухомій системи координат, а – її орти, то (д)Абсолютна швидкість точки, яка здійснює складний рух, дорівнює геометричній сумі її переносної і відносної швидкостей.
З попереднього (див. векторну рівність (е)) маємо Якщо цю рівність ще раз продиференціювати за часом, то отримаємоАбсолютне пришвидшення точки, яка здійснює складний рух, дорівнює геометричній сумі її переносного, відносного і коріолісового пришвидшень.
Якщо отриману формулу (2.59) порівняти з формулою (2.58), яка визначає абсолютну швидкість точки, що здійснює складний рух, то видно, що у формулі (2.59) з’явився додатковий член 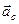 . Ось чому
. Ось чому 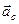 часто називають вектором додаткового пришвидшення.
часто називають вектором додаткового пришвидшення.
Коріолісове пришвидшення і його визначення
. (з) Для надання фізичного змісту отриманому виразу виконаємо деякі перетворення.… ; ; , (i)Вектор пришвидшення Коріоліса геометрично дорівнює подвійному векторному добутку вектора переносної кутової швидкості на вектор відносної лінійної швидкості.
Отримана формула (2.60) дає змогу визначити як величину, так і напрям вектора пришвидшення Коріоліса. Виходячи з властивості векторного добутку, маємо формулу

 , (2.61)
, (2.61)
яка визначає модуль коріолісового пришвидшення.
Модуль пришвидшення Коріоліса дорівнює подвійному добутку модуля кутової швидкості переносного руху () на модуль відносної лінійної швидкості () і на синус кута між цими векторами.
З формули (2.61) випливає, що коріолісове пришвидшен-ня дорівнює нулеві в таких випадках:
1) коли 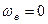 , тобто у випадку поступального переносного руху або в момент, коли кутова швидкість непоступального руху дорівнює нулеві;
, тобто у випадку поступального переносного руху або в момент, коли кутова швидкість непоступального руху дорівнює нулеві;
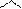 2) коли
2) коли 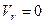 , тобто у момент часу відносного спокою точки;
, тобто у момент часу відносного спокою точки;
3) коли 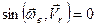 , тобто у випадку, коли
, тобто у випадку, коли 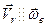 , а це означає, що вектор відносної швидкості точки паралельний до осі переносного обертання.
, а це означає, що вектор відносної швидкості точки паралельний до осі переносного обертання.
В кожному з цих випадків формула (2.59) набуває вигляду
 . (2.62)
. (2.62)
Оскільки другий і третій випадок отримуємо найчастіше тільки в деякий момент часу, то формулу (2.62) застосовують при визначенні пришвидшення точки, яка здійснює складний рух у випадку переносного поступального руху.
Отже,
Абсолютне пришвидшення точки, яка здійснює складний рух, у випадку переносного поступального руху дорівнює геометричній сумі її переносного і відносного пришвидшень.
 Напрям вектора пришвидшення Коріоліса можна визначити двома способами:
Напрям вектора пришвидшення Коріоліса можна визначити двома способами:
1. За правилом векторного добутку. Вектор коріолісового пришвидшення напрямлений перпендикулярно до площини, яка проходить через вектори  і
і  в бік, звідки поворот вектора
в бік, звідки поворот вектора  до вектора
до вектора  на найменший кут, щоб їх сумістити, видно проти ходу годинникової стрілки (рис.108).
на найменший кут, щоб їх сумістити, видно проти ходу годинникової стрілки (рис.108).
2. За правилом Жуковського. Для визначення напряму вектора коріолісового пришвидшення необхідно вектор відносної швидкості  спроектувати на площину, яка перпендикулярна до осі переносного обертання, і отриману проекцію в заданій площині повернути на кут 90° в бік переносного обертання. Це продемонстровано на рис. 109, де зображено:
спроектувати на площину, яка перпендикулярна до осі переносного обертання, і отриману проекцію в заданій площині повернути на кут 90° в бік переносного обертання. Це продемонстровано на рис. 109, де зображено:

 – вісь переносного обертання; по цій осі відкладено вектор
– вісь переносного обертання; по цій осі відкладено вектор  ;
;
Н – площина, яка перпендикулярна до осі  ;
;
 – вектор відносної швидкості точки;
– вектор відносної швидкості точки;
 – проекція вектора відносної швидкості на площину, яка перпендикулярна до осі переносного обертання;
– проекція вектора відносної швидкості на площину, яка перпендикулярна до осі переносного обертання;
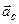 – вектор пришвидшення Коріоліса.
– вектор пришвидшення Коріоліса.
Правило Жуковського для визначення напряму вектора 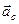 ефективно використовувати при плоскому складному русі, тобто тоді, коли складний рух точки відбувається в одній площині.
ефективно використовувати при плоскому складному русі, тобто тоді, коли складний рух точки відбувається в одній площині.
Виникнення пришвидшення Коріоліса, як показує аналіз складного руху точки, особливо у випадках, коли 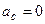 , пояснюється двома причинами.
, пояснюється двома причинами.
1. Відносний рух точки змінює величину вектора переносної швидкості.
2. Переносний рух точки змінює напрям вектора відносної швидкості.
Кожна з цих причин в абсолютне пришвидшення точки, яка здійснює складний рух, вносить свій додаток  , а пришвидшення Коріоліса дорівнює подвійному векторному добутку
, а пришвидшення Коріоліса дорівнює подвійному векторному добутку  на
на  , тобто
, тобто  .
.
Питання для самоконтролю
1. Який рух точки називається складним?
2. Який рух точки називається абсолютним?
3. Чи можна вважати складним рух штучного супутника навколо Землі? Обгрунтувати.
4. Наведіть два приклади складного руху точки.
5. Точка здійснює складний рух. Який рух точки називається переносним?
6. Який рух точки називається відносним?
7. Сформулюйте теорему про складання швидкостей точки в складному русі.
8. Запишіть формулу, яка визначає абсолютну швидкість точки, котра здійснює складний рух.
9. По вагону, що рухається з швидкістю  м/с, йде людина з швидкістю
м/с, йде людина з швидкістю  м/с. Який рух людини буде відносним? Яка швидкість відносного руху людини?
м/с. Який рух людини буде відносним? Яка швидкість відносного руху людини?
10. В деякий моменти часу точка має переносну швидкість 4 м/с, відносну швидкість 3 м/с. Визначити абсолютну швидкість точки, якщо кут між напрямами відносної і переносної швидкостей дорівнює 0°, 90°, 180°.
11. Сформулюйте теорему про складання пришвидшень точки в складному русі у випадку переносного поступального руху.
12. Запишіть формулу, за допомогою якої визначається величина пришвидшення Коріоліса.
13. Запишіть формулу, яка визначає вектор пришвидшення Коріоліса.
14. Сформулюйте теорему, за допомогою якої визначається пришвидшення точки в складному русі.
15. Запишіть формулу, за допомогою якої визначається пришвидшення токи в складному русі.
16. В яких випадках пришвидшення Коріоліса дорівнює нулю?
17. Як визначається напрям пришвидшення Коріоліса?
18. Точка здійснює складний рух. Вектор її відносної швидкості напрямлений вздовж осі абсцис. Вектор кутової швидкості переносного обертання напрямлений вздовж осі ординат. Знайти напрям вектора пришвидшення Коріоліса.
19. Чому дорівнює абсолютне пришвидшення точки, коли кут між  і
і  дорівнює 180°?
дорівнює 180°?
Кінематика складного руху твердого тіла
Складний рух твердого тіла
Складним рухом твердого тіла називається такий рух, при якому тіло одночасно здійснює два або декілька рухів.
Наприклад, автомобільне колесо здійснює складний рух: рухається поступально разом з автомобілем і одночасно обертається навколо своєї осі. Земля здійснює складний рух. Як відомо з астрономії, вона одночасно обертається навколо трьох осей, до того ж рухається по еліптичній орбіті навколо Сонця і т.д.
Фактично в природі всі тіла здійснюють складний рух.
Вивчення складного руху твердого тіла залежно від задач, які ставляться, можна проводити двома методами: методом аналізу або методом синтезу. Метод аналізу полягає в розкладанні заданого руху твердого тіла на прості (поступальний і обертальний) рухи. В методі синтезу складний рух твердого тіла отримується шляхом складання простих рухів. Як в першому, так і в другому методах всі кінематичні характеристики руху тіла визначаються через кінематичні характеристики складових рухів, що і є основним завданням кінематики складного руху тіла.
Плоскопаралельний (плоский) рух твердого тіла
Основні поняття і визначення
Плоскопаралельним (плоским) рухом твердого тіла називається такий його рух, при якому всі точки тіла рухаються в площинах, паралельних деякій нерухомій площині.
Частковим випадком плоскопаралельного руху є обертання твердого тіла навколо нерухомої осі, адже в даному русі, як відомо з попереднього, всі точки тіла рухаються в площинах, які перпендикулярні до осі обертання, тобто в паралельних площинах.
Більш загальним прикладом плоскопаралельного руху є рух призми (на рис. 110 зображено частковий випадок призми – паралелепіпед), основа якої довільно переміщається по нерухомій площині Н. При такому русі всі її точки переміщаються в площинах, паралельних площині Н. Плоскопаралельний рух широко розповсюджений в техніці. Переважна більшість механізмів, які зустрічаються на практиці, є сукупністю твердих тіл, що з’єднані між собою, і рухаються паралельно деякій площині, тобто здійснюють плоскопаралельний рух. Таким є, наприклад, рух окремих ланок кривошипно-шатун-ного механізму (рис. 111). Всі точки кожної з його ланок рухаються паралельно нерухомій площині (площині рисунка). Але плоский рух кривошипа ОА є обертальним, бо він має закріплену точку О . Плоский рух повзуна В є поступальним, тому що будь-яка пряма цього повзуна переміщається паралельно своєму початковому положенню. Рух шатуна АВ є найбільш загальним прикладом плоскопаралельного руху, бо його рух не є ні обертальним (оскільки шатун не має нерухомої точки), ні поступальним (оскільки пряма АВ не залишається при русі шатуна паралельною своєму початковому положенню).

Рис. 110

Рис. 111
А тепер детально проаналізуємо загальний випадок плоскопаралельного руху твердого тіла. Нехай точки тіла М рухаються паралельно деякій нерухомій площині Н (рис.112). Перетнемо тіло деякою площиною 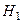 , що паралельна площині Н (Н1 | | Н). В перетині отримаємо плоску фігуру S. Ця плоска фігура при русі тіла буде переміщатися в площині
, що паралельна площині Н (Н1 | | Н). В перетині отримаємо плоску фігуру S. Ця плоска фігура при русі тіла буде переміщатися в площині 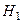 , тобто
, тобто  . Проведемо відрізок прямої АА перпендикулярно до плоскої фігури S. На цьому відрізку візьмемо дві точки
. Проведемо відрізок прямої АА перпендикулярно до плоскої фігури S. На цьому відрізку візьмемо дві точки 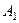 – точку перетину відрізка АА з плоскою фігурою S і
– точку перетину відрізка АА з плоскою фігурою S і 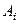 – довільну точку цього відрізка. При вказаному русі тіла відрізок АА буде здійснювати поступальний рух, тому що відстані точок цього відрізка до нерухомої площини Н не міняються, а це означає що відрізок АА залишається при русі перпендикулярним до площини Н, тобто паралельний сам собі. А це означає, що траєкторія точки
– довільну точку цього відрізка. При вказаному русі тіла відрізок АА буде здійснювати поступальний рух, тому що відстані точок цього відрізка до нерухомої площини Н не міняються, а це означає що відрізок АА залишається при русі перпендикулярним до площини Н, тобто паралельний сам собі. А це означає, що траєкторія точки 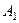 буде тотожна траєкторії точки
буде тотожна траєкторії точки 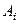 (
( ). Швидкості і пришвидшення цих точок геометрично рівні (
). Швидкості і пришвидшення цих точок геометрично рівні ( ,
,  ).
).
Тепер проведемо відрізок прямої ВВ перпендикулярно до плоскої фігури S. На цьому відрізку візьмемо дві точки:  – точку перетину відрізка ВВ з плоскою фігурою S і
– точку перетину відрізка ВВ з плоскою фігурою S і  – довільну точку цього відрізка. Аналогічно міркуючи, отримаємо, що траєкторія точки
– довільну точку цього відрізка. Аналогічно міркуючи, отримаємо, що траєкторія точки  тотожна траєкторії точки
тотожна траєкторії точки  . Швидкість і пришвидшення точки
. Швидкість і пришвидшення точки  геометрично рівні швидкості і пришвидшенню точки
геометрично рівні швидкості і пришвидшенню точки  (
( ).
).

Рис. 112
Через кожну точку плоскої фігури можна провести відповідні відрізки і отримати аналогічні висновки, тобто кінематичні характеристики руху точок кожного відрізка будуть співпадати (одинаковими) з кінематичними характеристиками руху точки перетину відповідного відрізка з плоскою фігурою.
Отже,
Плоскопаралельний рух твердого тіла цілком визначається рухом його плоскої фігури.
Таким чином, вивчення плоскопаралельного руху твердого тіла зводиться до вивчення руху його плоскої фігури, яка утворюється шляхом перетину тіла площиною, що паралельна до площини, паралельно якій рухається тіло.
Рівняння руху плоскої фігури
(2.63) Рівняння (2.63), за допомогою яких можна визначити положення плоскої фігури в…Рис. 113
Розглянемо часткові випадки:
1. Припустимо, що плоска фігура здійснює рух, при якому

В даному випадку при русі плоскої фігури відрізок ОА буде паралельним своєму початковому положенню, а це означає, що плоска фігура здійснює поступальний рух.
2. У випадку, коли

плоска фігура, очевидно, буде здійснювати обертальний рух.
При русі плоскої фігури одночасно змінюються три параметри (див. рівняння 2.63). Таким чином, можна стверджувати, що:
Плоскопаралельний рух твердого тіла є складним рухом; він складається з поступального і оберталь-ного рухів.
Точка, з якою плоска фігура здійснює поступальний рух, називається полюсом.
– положення плоскої фігури після поступального її переміщення з положення І в положення ІІ у випадку, коли за плюс вибрано точку ; – положення плоскої фігури після поступального її переміщення з положення І в… – кути повороту плоскої фігури навколо відповідних полюсів.Рис. 114
Поступальний рух плоскої фігури залежить від вибору полюса, а обертальний її рух не залежить від вибору полюса.
Зауваження:
1. Додатний напрям кута 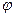 вибирається проти ходу годинникової стрілки.
вибирається проти ходу годинникової стрілки.
2. Модулі кутової швидкості і пришвидшення дорівнюють
 ;
;  .
.
3. Вектори  і
і 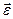 направляються перпендикулярно до площини руху згідно з правилом, запропонованим при обертальному русі тіла (§ 43.4). Вектори
направляються перпендикулярно до площини руху згідно з правилом, запропонованим при обертальному русі тіла (§ 43.4). Вектори  і
і 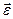 є вільними векторами і можуть бути прикладені в будь-якій точці плоскої фігури.
є вільними векторами і можуть бути прикладені в будь-якій точці плоскої фігури.
Рівняння руху точки плоскої фігури
; . Розкривши косинус і синус суми двох кутів,Рис. 115
і враховуючи, що  ,
, 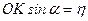 , отримуємо
, отримуємо
 (2.64)
(2.64)
Рівняння (2.64) є рівняннями руху точки плоскої фігури. В цих рівняннях  і
і 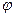 змінюються за законами (2.63),
змінюються за законами (2.63), 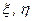 – координати точки в системі координат, яка жорстко з’єднана з плоскою фігурою і для точки вони є постійними.
– координати точки в системі координат, яка жорстко з’єднана з плоскою фігурою і для точки вони є постійними.
Користуючись формулами (2.8) – (2.13), і (2.64), можна аналогічно знайти швидкість і пришвидшення будь-якої точки плоскої фігури, тобто:
 ,
,  .
.
Тут
 ;
;  ;
;
 ;
;
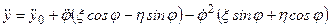 .
.
Напрямні косинуси векторів  і
і 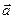 знаходяться за формулами
знаходяться за формулами

 ;
;  ;
;

 ;
;  .
.
Векторний спосіб знаходження швидкостей і пришвидшень точок плоскої фігури розглянуті в наступних параграфах.
Теорема про швидкості точок плоскої фігури та її наслідок
Нехай полюс рухається з швидкістю , і навколо полюса плоска фігура обертається з кутовою швидкістю . Візьмемо довільну точку К плоскої фігури,… . (а) Прийнявши поступальний рух плоскої фігури за переносний рух, отримаємо, що переносні швидкості всіх точок плоскої…Швидкість будь-якої точки плоскої фігури дорівнює геометричній сумі швидкості полюса і обертальної швидкості даної точки навколо полюса.
Вектор швидкості визначається за законами обертального руху, тобто його величина дорівнює , і він напрямлений перпендикулярно до відрізка КО в бік… З доведеної теореми випливає наслідок:Проекції швидкостей двох точок плоскої фігури на вісь, яка проходить через ці дві точки, рівні між собою.
Для доведення цього наслідку розглянемо дві довільні точки А і В плоскої фігури, яка рухається у площині рисунка. Вектори швидкостей цих точок  і
і 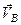 (рис. 118) утворюють з прямою АВ відповідно кути
(рис. 118) утворюють з прямою АВ відповідно кути 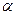 і
і  . Приймаючи точку А за полюс, швидкість точки В згідно з (2.65) буде визначатися формулою
. Приймаючи точку А за полюс, швидкість точки В згідно з (2.65) буде визначатися формулою
 . (г)
. (г)
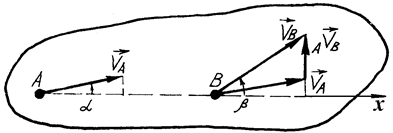
Рис. 118
Проектуючи векторну рівність (г) на вісь Ах і знаючи, що  , матимемо
, матимемо
 .
.
Оскільки  , отримаємо
, отримаємо
 ,
,
тобто
 . (2.66)
. (2.66)
Отже, наслідок доведено. Цей наслідок часто називають теоремою про проекції швидкостей точок плоскої фігури. Необхідно пам’ятати, що ця теорема має місце тільки тоді, коли вектори швидкостей точок плоскої фігури проектуємого на вісь, яка проходить через ці точки. Треба зазначити, що формула (2.66) має місце для будь-якого руху твердого тіла, що легко довести, скориставшись залежністю (2.31).
Миттєвий центр швидкостей
Точка твердого тіла під час плоского руху, швидкість якої в даний момент часу дорівнює нулеві, називається миттєвим центром швидкостей.
Для цього розглянемо плоску фігуру, яка виконує деякий рух у площині рисунка (рис. 119). За полюс плоскої фігури візьмемо точку О, швидкість якої .… . (а) Обертальна швидкість точки Р навколо полюса О за величиною дорівнюєШвидкість будь-якої точки плоскої фігури є обертальною швидкістю навколо миттєвого центра швидкостей
З отриманого результату випливає:
1. Оскільки  , то і
, то і 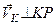 .
.
Оскільки К – довільна точка плоскої фігури, то маємо, що
Вектори швидкостей точок плоскої фігури перпендикулярні до відрізків, що з’єднують відповідні точки з миттєвим центром швидкостей.
2. За формулою обертальної швидкості  з (2.68) отримуємо
з (2.68) отримуємо
 . (2.69)
. (2.69)
Швидкість будь-якої точки плоскої фігури чисельно дорівнює добутку кутової швидкості на відстань даної точки до миттєвого центра швидкостей.
3. Формулу (2.69) можна застосувати для визначення швидкості будь-якої точки плоскої фігури. Для точок А, В і С матимемо
 ,
,
 ,
,
 .
.
Звідси отримуємо, що
 . (2.70)
. (2.70)
Швидкості точок плоскої фігури пропорційні відстаням даних точок до миттєвого центра швидкостей. Коефіцієнт пропорційності дорівнює кутовій швидкості плоскої фігури.
Формули (2.68)-(2.70) визначають швидкості точок плоскої фігури за допомогою миттєвого центра швидкостей. На основі цих формул можна зобразити розподіл (еп’юр) швидкостей точок плоскої фігури. Цей розподіл має вигляд, який зображений на рис. 120. На цьому рисунку показано: Р – миттєвий центр швидкостей плоскої фігури; вектори швидкостей точок плоскої фігури, які перпендикулярні до відрізків, що з’єднують відповідні точки з миттєвим центром швидкостей; величини їх пропорційні відстаням даних точок до миттєвого центра швидкостей. Цей розподіл відповідає розподілу швидкостей точок тіла, яке обертається навколо нерухомої осі,  тобто, в кожний момент часу швидкості точок плоскої фігури розподілені так, немов би фігура обертається навколо точки Р. Саме тому миттєвий центр швидкостей плоскої фігури називають миттєвим центром її повороту. До того ж є відповідна теорема (див. теорему Шаля), згідно з якою:
тобто, в кожний момент часу швидкості точок плоскої фігури розподілені так, немов би фігура обертається навколо точки Р. Саме тому миттєвий центр швидкостей плоскої фігури називають миттєвим центром її повороту. До того ж є відповідна теорема (див. теорему Шаля), згідно з якою:
1. Плоску фігуру можна перемістити з одного положення в будь-яке інше шляхом одного повороту навколо деякої точки, яка називається центром повороту.
2. Граничне положення центра повороту, тобто положення центра повороту для нескінченно малого переміщення плоскої фігури, є не що інше, як миттєвий центр швидкостей плоскої фігури.
Способи визначення положення миттєвого центра швидкостей
З попереднього відомо, що миттєвий центр швидкостей знаходиться на перпендикулярі, поставленому до вектора швидкості полюса. Звідси випливає, що,… Інші часткові випадки знаходження положення миттєвого центра швидкостей…Рис. 122
Всі вони відповідають основним положенням, які були сформульовані вище.
Зазначимо, що у випадку, зображеному на рис. 122 в, миттєвий центр швидкостей плоскої фігури знаходиться в нескінченності. Кутова швидкість плоскої фігури, яка визначається за формулою (див. 2.70)
 , або
, або  ,
,
буде дорівнювати нулеві. Це означає, що обертальні швидкості всіх точок плоскої фігури навколо полюса дорівнюють нулеві. Звідси випливає, що швидкість всіх точок плоскої фігури дорівнюють швидкості полюса, тобто в даний момент часу плоска фігура буде здійснювати миттєво поступальний рух. Для цього руху швидкості всіх точок плоскої фігури геометрично рівні
 ,
,
а пришвидшення загалом різні
 .
.
Якщо плоска фігура котиться по нерухомій поверхні без ковзання (наприклад, колесо – рис. 123), то її миттєвий центр  швидкостей знаходиться в точці дотику плоскої фігури з нерухомою поверхнею. Адже ця точка одночасно належить плоскій фігурі і поверхні, і її швидкість в даний момент дорівнює нулеві, бо поверхня нерухома. При русі плоскої фігури положення миттєвого центра швидкостей змінюється.
швидкостей знаходиться в точці дотику плоскої фігури з нерухомою поверхнею. Адже ця точка одночасно належить плоскій фігурі і поверхні, і її швидкість в даний момент дорівнює нулеві, бо поверхня нерухома. При русі плоскої фігури положення миттєвого центра швидкостей змінюється.
Геометричне місце послідовних положень на площині миттєвого центра швидкостей (або лінія, яка описується миттєвим центром швидкостей) називається центроїдою.
 В плоскопаралельному русі розрізняють дві центроїди: рухому і нерухому (рис. 124).
В плоскопаралельному русі розрізняють дві центроїди: рухому і нерухому (рис. 124).
Нерухома центроїда – це лінія, яка описується миттєвим центром швидкостей в нерухомій площині.
Рухома центроїда – це лінія, яка описується миттєвим центром швидкостей в рухомій площині, яка з’єднана з плоскою фігурою. При русі плоскої фігури рухома центроїда котиться без ковзання по нерухомій центроїді (рис. 124).
Теорема про пришвидшення точок плоскої фігури
Візьмемо довільну точку К плоскої фігури, положення якої відносно полюса О визначається радіусом-вектором , і визначимо її пришвидшення. Оскільки рух плоскої фігури є складним рухом, який складається з поступального… . (а)Пришвидшення будь-якої точки плоскої фігури дорівнює геометричній сумі пришвидшення полюса і пришвидшення даної точки в обертанні навколо полюса.
Формулу (2.71) з врахуванням залежності (г) можна представити і так:
 . (2.72)
. (2.72)
Пришвидшення будь-якої точки плоскої фігури дорівнює геометричній сумі трьох пришвидшень: при-швидшення полюса, обертального і доцентрового пришвидшень даної точки в обертанні навколо полюса.
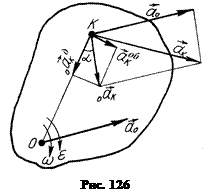 Отримані формули (2.71) або (2.72) виражають теорему про пришвидшення точок плоскої фігури. Отже, згідно з даною теоремою, щоб знайти пришвидшення деякої точки плоскої фігури, необхідно мати пришвидшення полюса і визначити пришвидшення даної точки в обертанні навколо полюса. Останнє складається з доцентрового пришвидшення, величина якого обчислюються за формулою (див. формулу 2.46)
Отримані формули (2.71) або (2.72) виражають теорему про пришвидшення точок плоскої фігури. Отже, згідно з даною теоремою, щоб знайти пришвидшення деякої точки плоскої фігури, необхідно мати пришвидшення полюса і визначити пришвидшення даної точки в обертанні навколо полюса. Останнє складається з доцентрового пришвидшення, величина якого обчислюються за формулою (див. формулу 2.46)

і вектор якого напрямлений від точки К до полюса, і обертального пришвидшення, величина якого обчислюється за формулою (див. 2.47)
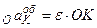
і вектор якого напрямлений перпендикулярно до відрізка ОК в бік кутового пришвидшення (рис. 126). Геометрично склавши  і
і  , отримаємо пришвидшення точки в обертальному русі навколо полюса О, величина якого знаходиться за формулою
, отримаємо пришвидшення точки в обертальному русі навколо полюса О, величина якого знаходиться за формулою
 . (2.73)
. (2.73)
Цей вектор утворює кут 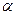 з відрізком ОК. Тангенс цього кута визначається за формулою
з відрізком ОК. Тангенс цього кута визначається за формулою
 . (2.74)
. (2.74)
Вектор загального пришвидшення  точки К є діагональ паралелограма, побудованого на векторах пришвидшень
точки К є діагональ паралелограма, побудованого на векторах пришвидшень  і
і  (рис. 126).
(рис. 126).
Миттєвий центр пришвидшень
Миттєвим центром пришвидшень називається точка під час плоского руху тіла, пришвидшення якої в даний момент часу дорівнює нулеві.
Покажемо, що в кожний момент часу існує точка плоскої фігури, пришвидшення якої в цей момент часу дорівнює нулеві. Для цього розглянемо плоску фігуру, котра рухається в площині рисунка (рис.… . (а)Рис. 130
Згідно з формулою (2.71)
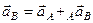 .
.
Будуємо в точці В паралелограм прискорень за заданою діагоналлю  і однією стороною
і однією стороною  . За знайденим графічно при-швидшенням
. За знайденим графічно при-швидшенням  визначаємо напрям
визначаємо напрям 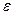 і кут
і кут 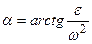 , який цей вектор утворює з відрізком АВ. Маючи кут
, який цей вектор утворює з відрізком АВ. Маючи кут 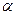 і напрям
і напрям 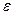 , відкладаємо цей кут від пришвидшень точок А і В по напряму
, відкладаємо цей кут від пришвидшень точок А і В по напряму 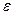 . Отримані два промені продовжуємо до перетину в точці
. Отримані два промені продовжуємо до перетину в точці  , яка буде миттєвим центром пришвидшень.
, яка буде миттєвим центром пришвидшень.
На рисунку 131 побудовані миттєві центри пришвидшень у випадку, коли  і
і  паралельні.
паралельні.

Рис. 131
1. Випадки а) і б) відповідають  , тобто
, тобто
 ;
;  .
.
2. Випадки в) і г) відповідають  , тобто
, тобто 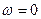 ;
;  .
.
3. Випадки д) і е) відповідають  , тобто
, тобто  ;
; 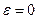 .
.
4. У випадку є) 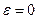 і
і 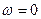 миттєвий центр пришвидшень знаходиться в нескінченності, а пришвидшення всіх точок плоскої фігури геометрично рівні.
миттєвий центр пришвидшень знаходиться в нескінченності, а пришвидшення всіх точок плоскої фігури геометрично рівні.
Якщо відомий миттєвий центр пришвидшень, то знаходження пришвидшень точок плоскої фігури суттєво спрощується. Дійсно, прийнявши миттєвий центр пришвидшень  за полюс (рис. 132), отримаємо
за полюс (рис. 132), отримаємо
 .
.

Рис. 132
Оскільки 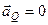 , то
, то  . Аналогічно
. Аналогічно 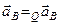 ,
,  . Із цих співвідношень згідно з (2.73) отримаємо
. Із цих співвідношень згідно з (2.73) отримаємо
 ;
;
 ; (2.76 а)
; (2.76 а)
 .
.
Отже, якщо відомий миттєвий центр пришвидшень, то пришвидшення точки плоскої фігури в кожний момент часу обчислюється за формулою (2.76 а).
Пришвидшення точок плоскої фігури пропорційні відстані від точок до миттєвого центра пришвид-шень, а вектори пришвидшень утворюють з відрізками, які з’єднують ці точки з миттєвим центром пришвидшень один і той же кут .
Зауваження. Миттєвий центр швидкостей Р і миттєвий центр пришвидшень Q є різні точки плоскої фігури.
Питання для самоконтролю
1. Який рух твердого тіла називається плоскопаралельним?
2. Запишіть рівняння руху плоскої фігури.
3. Що називається полюсом плоскої фігури?
4. З яких простих рухів складається плоскопаралельний рух твердого тіла?
5. Який складовий рух плоскої фігури залежить від вибору полюса, а який не залежить?
6. Запишіть рівняння руху точки плоскої фігури.
7. Сформулюйте теорему про швидкості точок плоскої фігури.
8. Сформулюйте теорему про проекції векторів швидкостей точок плоскої фігури.
 9. Знайдіть швидкість точки В фігури, котра рухається в площині рисунка, якщо
9. Знайдіть швидкість точки В фігури, котра рухається в площині рисунка, якщо  м/с,
м/с,  с–1, ОА=0,5м.
с–1, ОА=0,5м.
10. Визначіть швидкість точки А плоскої фігури, котра рухається в площині рисунка, якщо  м/с,
м/с,  с-1, ОА=0,5 м.
с-1, ОА=0,5 м.
11. Що називається миттєвим центром швидкостей?
12. Як знайти положення миттєвого центра швидкостей, знаючи напрями векторів швидкостей двох точок плоскої фігури?
13. Як знайти положення миттєвого центра швидкостей плоскої фігури, знаючи швидкість якої-небудь її точки і кутову швидкість плоскої фігури.
14. В деякий момент часу швидкість точки А плоскої фігури дорівнює 10 м/с, її відстань до миттєвого центра швидкостей 4 м. Чому дорівнює в даний момент часу кутова швидкість плоскої фігури?
15. Для плоскої фігури в деякий момент часу відомо  м/с, АР = 3 м, ВР = 4 м, де Р – миттєвий центр швидкостей плоскої фігури. Знайти величину швидкості точки В.
м/с, АР = 3 м, ВР = 4 м, де Р – миттєвий центр швидкостей плоскої фігури. Знайти величину швидкості точки В.
16. Сформулюйте теорему про пришвидшення точок плоскої фігури.
17. Запишіть формулу, за допомогою якої визначається пришвидшення точки плоскої фігури.
18. Що називається миттєвим центром пришвидшень?
19. Запишіть формули, за допомогою яких визначається положення миттєвого центра пришвидшень плоскої фігури.
20. В деякий момент часу для плоскої фігури маємо 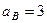 м/с2,
м/с2,  с–1,
с–1, 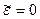 . Визначіть положення її миттєвого центра пришвидшень.
. Визначіть положення її миттєвого центра пришвидшень.
21. В деякий момент часу для плоскої фігури маємо  м/с2,
м/с2,  ,
,  с–2. Визначіть положення її миттєвого центра пришвидшень.
с–2. Визначіть положення її миттєвого центра пришвидшень.
22. Для плоскої фігури, яка зображена на рисунку, знайти положення миттєвого центра пришвидшень, якщо її кутова швидкість в даний момент часу 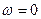 . (рис. А).
. (рис. А).
23. Визначіть кутове пришвидшення колеса, котре коти-ться без ковзання по нерухомій поверхні, якщо  . (рис. Б).
. (рис. Б).
 Рис. А
Рис. А
|  Рис. Б
Рис. Б
|
Обертання твердого тіла навколо нерухомої точки
Обертанням твердого тіла навколо нерухомої точки називається такий його рух, при якому протягом усього часу руху одна точка тіла залишається нерухомою.
Цей рух часто називають сферичним, оскільки траєкторії всіх точок тіла розміщаються на поверхнях сфер, центри яких знаходяться у нерухомій точці.
Вільне тверде тіло має шість ступенів вільності. Закріплення однієї точки тіла зменшує число ступенів вільності на три одиниці, а це означає, що тіло, котре обертається навколо нерухомої точки, має три ступені вільності. Отже, для однозначного визначення його положення в просторі необхідні як мінімум три параметри. Їх можна вибрати по-різному. В теоретичній механіці, як і в більшості дисциплін, найбільш широке застосування отримали кути, які були запропоновані Ейлером.
Кути Ейлера. Рівняння обертання твердого тіла навколо нерухомої точки
(псі), (фі) , (тета) , причому вважаємо кути додатними у тому випадку, якщо для спостерігача, що…Рис. 133
Заданням кутів  однозначно визначається положення осей
однозначно визначається положення осей  , отже і положення тіла. І дійсно:
, отже і положення тіла. І дійсно:
1. Відклавши в нерухомій координатній площині 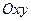 кут
кут  , як вказано на рис. 133, отримаємо положення лінії вузлів ON.
, як вказано на рис. 133, отримаємо положення лінії вузлів ON.
2. Провівши перпендикулярно до лінії вузлів ON через вісь Oz площину і відклавши в цій площині кут  , як вказано на рис. 133, отримаємо положення осі
, як вказано на рис. 133, отримаємо положення осі  .
.
3. Якщо через лінію вузлів перпендикулярно до осі  провести площину і в заданій площині від лінії вузлів ON відкласти кут
провести площину і в заданій площині від лінії вузлів ON відкласти кут 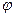 , як вказано на рис. 133, то отримаємо положення осі
, як вказано на рис. 133, то отримаємо положення осі  . Вісь
. Вісь  знаходиться в цій же площині і складає разом з осями
знаходиться в цій же площині і складає разом з осями  і
і  праву систему координат.
праву систему координат.
Таким чином, кути  повністю, до того ж однозначно, визначають положення рухомої системи. Кути
повністю, до того ж однозначно, визначають положення рухомої системи. Кути  називаються кутами Ейлера. Крім того, кожний з них має свою назву, що визначається обертанням, яке буде здійснювати тіло при зміні відповідного кута. Так, кут
називаються кутами Ейлера. Крім того, кожний з них має свою назву, що визначається обертанням, яке буде здійснювати тіло при зміні відповідного кута. Так, кут 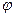 називається кутом власного обертання, бо при зміні цього кута тіло обертається, як вказано на рис. 134, навколо осі
називається кутом власного обертання, бо при зміні цього кута тіло обертається, як вказано на рис. 134, навколо осі  .
.  – це кут прецесії. При зміні цього кута тіло обертається (див. рис. 134) навколо осі Oz, тобто вісь
– це кут прецесії. При зміні цього кута тіло обертається (див. рис. 134) навколо осі Oz, тобто вісь  обертається (прецесує) навколо осі Oz.
обертається (прецесує) навколо осі Oz.  – називається кутом нутації. При зміні даного кута тіло обертається, як вказано на рис. 134, навколо лінії вузлів ON.
– називається кутом нутації. При зміні даного кута тіло обертається, як вказано на рис. 134, навколо лінії вузлів ON.

Рис. 134
Якщо тверде тіло виконує обертальний рух навколо нерухомої точки О, то кути  безперервно змінюються з часом, тобто є деякими функціями часу
безперервно змінюються з часом, тобто є деякими функціями часу
 ;
;  ;
;  . (2.77)
. (2.77)
Записані рівняння, що цілком визначають обертальний рух твердого тіла навколо нерухомої точки, називаються кінематичними рівняннями руху твердого тіла навколо нерухомої точки. Вони визначають закон руху тіла.
Теорема Ейлера-Даламбера
Як видно з попереднього, обертання тіла навколо нерухомої точки складається з обертань трьох осей  . Виходячи з цього, можна отримати відповідні формули для визначення кінематичних характеристик руху тіла і його точок. Отримати дані формули можна і іншим шляхом. Для цього розглянемо теорему Ейлера-Даламбера:
. Виходячи з цього, можна отримати відповідні формули для визначення кінематичних характеристик руху тіла і його точок. Отримати дані формули можна і іншим шляхом. Для цього розглянемо теорему Ейлера-Даламбера:
Усяке переміщення твердого тіла, що має одну нерухому точку, можна здійснити шляхом одного повороту навколо деякої осі, що проходить через нерухому точку.

 Для доведення даної теореми зауважимо, що положення твердого тіла в просторі однозначно визначається положенням трьох його точок, які не лежать на одній прямій. І дійсно (рис. 135), положення двох точок А і В тіла визначає положення деякої осі тіла Аz, а положення третьої точки С – кут повороту тіла відносно даної осі. До того ж при закріпленні даних точок тіло стане нерухомим, тобто займе деяке конкретне положення, що є ще одним підтверд-женням, що положення тіла в просторі цілком визначається положенням трьох його точок.
Для доведення даної теореми зауважимо, що положення твердого тіла в просторі однозначно визначається положенням трьох його точок, які не лежать на одній прямій. І дійсно (рис. 135), положення двох точок А і В тіла визначає положення деякої осі тіла Аz, а положення третьої точки С – кут повороту тіла відносно даної осі. До того ж при закріпленні даних точок тіло стане нерухомим, тобто займе деяке конкретне положення, що є ще одним підтверд-женням, що положення тіла в просторі цілком визначається положенням трьох його точок.
Перейдемо тепер до доведення сформульованої вище теореми. Для цього розглянемо деяке тверде тіло, яке обертається навколо нерухомої точки О (рис. 136). Положення тіла будемо визначати положенням трьох його точок: О – нерухома точка; А і В – дві довільні точки тіла, що знаходяться від нерухомої точки на однаковій відстані (ОА=ОВ), але не лежить з нею на одній прямій. Проведемо через ці точки сферу з центром в точці О.
Через точки А і В проведемо дугу 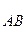 великого кола (дуга великого кола – це дуга кола, центр якого знаходиться в нерухомій точці О). Оскільки точка О нерухома, то положення тіла буде визначатись положенням дуги
великого кола (дуга великого кола – це дуга кола, центр якого знаходиться в нерухомій точці О). Оскільки точка О нерухома, то положення тіла буде визначатись положенням дуги 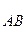 .
.
Припустимо, що в момент часу 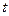 тіло займає положення
тіло займає положення 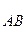 , а в момент часу
, а в момент часу 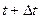 – положення
– положення  , тобто за деякий проміжок часу
, тобто за деякий проміжок часу 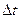 тіло перемістилось з положення
тіло перемістилось з положення 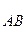 в положення
в положення  . Проведемо дуги
. Проведемо дуги  і
і  великих кіл.
великих кіл.
Через точки Е і К, які ділять відповідно  і
і  навпіл, проведемо перпендикулярно до даних дуг дуги великих кіл. Позначимо Н точку перетину щойно проведених дуг і з’єднаємо її дугами великих кіл з точками А, В, А1, В1. Отримаємо (на рис. 136 вони заштриховані) сферичні трикутники АВН і А1В1Н, які є рівними за рівністю трьох сторін:
навпіл, проведемо перпендикулярно до даних дуг дуги великих кіл. Позначимо Н точку перетину щойно проведених дуг і з’єднаємо її дугами великих кіл з точками А, В, А1, В1. Отримаємо (на рис. 136 вони заштриховані) сферичні трикутники АВН і А1В1Н, які є рівними за рівністю трьох сторін:
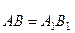 , бо в твердому тілі відстані між точками зберігаються;
, бо в твердому тілі відстані між точками зберігаються;
 – це випливає з рівності сферичних прямокутних трикутників АЕН і А1ЕН, в яких сторона ЕН є спільною
– це випливає з рівності сферичних прямокутних трикутників АЕН і А1ЕН, в яких сторона ЕН є спільною  – за побудовою;
– за побудовою;
 – це випливає з рівності сферичних прямокутних трикутників ВКН і В1КН, в яких сторона КН є спільною, а
– це випливає з рівності сферичних прямокутних трикутників ВКН і В1КН, в яких сторона КН є спільною, а  – за побудовою.
– за побудовою.
В рівних трикутниках відповідні кути є рівними, отже
 .
.
Додаючи до обох частин цієї рівності по куту 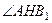 , отримаємо
, отримаємо

або
 .
.
Отже, при переміщенні тіла з положення АВ в положення 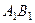 для суміщення точок
для суміщення точок  з
з 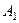 і
і  з
з  достатньо здійснити обертальний рух на один і той же кут
достатньо здійснити обертальний рух на один і той же кут  , а це означає, що все тіло як одне ціле повернуте на той же кут
, а це означає, що все тіло як одне ціле повернуте на той же кут  . При такому повороті залишаються нерухомими дві точки: точка О і точка Н. Вісь
. При такому повороті залишаються нерухомими дві точки: точка О і точка Н. Вісь  , яка проходить через ці точки, також буде нерухомою. Таким чином, переміщення тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі
, яка проходить через ці точки, також буде нерухомою. Таким чином, переміщення тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі  на кут
на кут  . Вісь
. Вісь  називається віссю кінцевого повороту, а кут
називається віссю кінцевого повороту, а кут  – кутом кінцевого повороту.
– кутом кінцевого повороту.
Якщо усяке переміщення твердого тіла, що має нерухому точку, можна здійснити шляхом одного повороту навколо осі кінцевого повороту, то, очевидно, і нескінченно мале його переміщення також може бути здійснене таким чином. При наближенні нескінченно малого переміщення до нуля положення тіла наближається до його першого положення. Разом з тим вісь  наближається до деякого граничного положення
наближається до деякого граничного положення 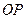 , яке називається миттєвою віссю обертання для заданого моменту часу.
, яке називається миттєвою віссю обертання для заданого моменту часу.
Отже, в кожний момент часу 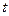 обертання твердого тіла навколо нерухомої точки можна розглядати як обертання навколо миттєвої осі, яка проходить через нерухому точку.
обертання твердого тіла навколо нерухомої точки можна розглядати як обертання навколо миттєвої осі, яка проходить через нерухому точку.
Для кожного моменту часу миттєва вісь обертання займає своє положення, і з часом описує конічну поверхню.
Конічна поверхня, яка описується миттєвою віссю обертання в нерухомому просторі (в просторі системи координат Оxyz), називається нерухомим аксоїдом.
Конічна поверхня, яка описується миттєвою віссю обертання в рухомому просторі (в просторі системи координат Oxhz ), називається рухомим аксоїдом.
При обертанні тіла навколо нерухомої точки рухомий аксоїд, змінюючи своє положення, рухається по поверхні нерухомого аксоїда.
Кутова швидкість і кутове пришвидшення тіла, що обертається навколо нерухомої точки
Оскільки обертання тіла навколо нерухомої точки в кожний момент часу можна вважати обертанням навколо миттєвої осі, то
Кутова швидкість, з якою в кожний момент часу тіло, що має нерухому точку, обертається навколо миттєвої осі, називається кутовою швидкістю тіла в даний момент часу.
 Вектор кутової швидкості
Вектор кутової швидкості  відкладається з нерухомої точки вздовж миттєвої осі обертання в той бік, звідки обертання тіла видно проти руху годинникової стрілки (рис. 137).
відкладається з нерухомої точки вздовж миттєвої осі обертання в той бік, звідки обертання тіла видно проти руху годинникової стрілки (рис. 137).
Оскільки при русі точки навколо нерухомої точки не існує такого кута як функції часу, похідна від якого дорівнювала б кутовій швидкості, то кутова швидкість повинна бути задана як функція часу або вона може бути представлена через кути Ейлера і їх похідні.
Як було показано в § 47.1, при русі тіла з однією закріпленою точкою воно одночасно обертається навколо трьох осей, що перетинаються (рис. 138), з кутовими швидкостями  ;
;  і
і  .
.
При такому русі тіла, як буде показано в § 49.3, формула (2.103), вектор результуючої миттєвої кутової швидкості дорівнює
 . (а)
. (а)
Для знаходження величини і напряму вектора кутової швидкості  визначимо його проекції на осі рухомої системи координат
визначимо його проекції на осі рухомої системи координат 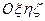 .
.

Рис. 138
Проектуючи обидві частини рівності (а) на осі  ,
,  ,
,  , отримаємо
, отримаємо
 ;
;
 ; (б)
; (б)
 .
.
Проекції векторів  і
і  знаходяться безпосереднім проектуванням (рис. 138)
знаходяться безпосереднім проектуванням (рис. 138)
 ;
; 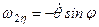 ;
;  ;
;
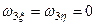 ;
;  ,
,
а для знаходження проекції вектора  проведемо через осі
проведемо через осі  і
і  площину, яка перетнеться з площиною
площину, яка перетнеться з площиною 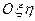 вздовж лінії
вздовж лінії  . Оскільки лінія вузлів
. Оскільки лінія вузлів 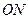 перпендикулярна до площини
перпендикулярна до площини  , то вона перпендикулярна і до лінії
, то вона перпендикулярна і до лінії  , а
, а  . Тоді, проектуючи вектор
. Тоді, проектуючи вектор  на площину
на площину 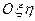 (проекція лежатиме на лінії
(проекція лежатиме на лінії  ), а одержану проекцію, в свою чергу, на осі
), а одержану проекцію, в свою чергу, на осі  і
і  , отримаємо
, отримаємо
 .
.
Підставляючи одержані проекції в праві частини рівностей (б), отримаємо
 ;
;
 ; (2.78)
; (2.78)
 .
.
Аналогічно проектуючи рівність (а) на осі нерухомої системи координат 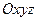 , знайдемо проекції вектора
, знайдемо проекції вектора  на ці осі
на ці осі
 ;
;
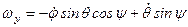 ; (2.78 а)
; (2.78 а)
 .
.
Рівності (2.78) і (2.78 а) називаються кінематичними рівняннями Ейлера. Вони дають можливість знайти модуль миттєвої кутової швидкості і напрямні косинуси вектора  з відповідними осями координат
з відповідними осями координат
 ;
;

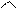

 ;
; 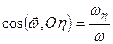 ;
;  ;
;

 ;
;  ;
;  .
.
Перша похідна за часом від вектора кутової швидкості називається вектором кутового пришвидшення
Вектор кутового пришвидшення також відкладають з нерухомої точки , навколо якої обертається тіло, але цей вектор (на відміну від обертання тіла… Напрям і величину вектора кутового пришвидшення можна знайти таким способом.… Вектор визначає положення точки в просторі, отже для даної точки він є радіусом-вектором, а це означає, щоВектор кутового пришвидшення тіла, котре обертається навколо нерухомої точки, геометрично до-рівнює вектору швидкості точки, яка описує годо-граф вектора кутової швидкості.
Отже, вектор кутового пришвидшення 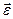 , який, як було сказано вище, відкладається з нерухомої точки, є паралельним вектору
, який, як було сказано вище, відкладається з нерухомої точки, є паралельним вектору  , котрий напрямлений вздовж дотичної до годографа вектора кутової швидкості (рис. 139). Рівність (2.80) часто використовують для визначення кутового пришвидшення тіла, яке обертається навколо нерухомої точки. Для цього, використовуючи відомі способи, визначають величину і напрям вектора швидкості, який описує годограф вектора кутової швидкості. Величина і напрям вектора
, котрий напрямлений вздовж дотичної до годографа вектора кутової швидкості (рис. 139). Рівність (2.80) часто використовують для визначення кутового пришвидшення тіла, яке обертається навколо нерухомої точки. Для цього, використовуючи відомі способи, визначають величину і напрям вектора швидкості, який описує годограф вектора кутової швидкості. Величина і напрям вектора  визначає величину і напрям вектора
визначає величину і напрям вектора 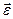 .
.
Пряму  (рис. 139), вздовж якої напрямлений вектор
(рис. 139), вздовж якої напрямлений вектор 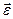 , можна назвати миттєвою лінією кутового пришвидшення.
, можна назвати миттєвою лінією кутового пришвидшення.
Величину і напрям кутового пришвидшення можна також знайти аналітично за допомогою формул
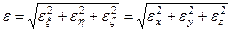 ;
;

 ;
;  ;
;  ;
;



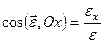 ;
;  ;
; 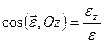 ,
,
де  ;
;  ;
;  ;
;  ;
;  ;
;  .
.
Швидкість точок твердого тіла, яке обертається навколо нерухомої точки
, (а) в якій: – вектор кутової швидкості тіла; – радіус-вектор точки, швидкість якої… З визначення векторного добутку безпосередньо випливає:Швидкість точки тіла, яке обертається навколо нерухомої точки, чисельно дорівнює добутку кутової швидкості тіла на відстань даної точки до миттєвої осі обертання.
Формулу (2.81) використовують не тільки для визначення швидкості точки тіла, яке здійснює сферичний рух. Її часто використовують і для визначення кутової швидкості самого тіла. Для цього шукають точку, швидкість якої можна визначити, не застосовуючи формулу (2.81). Знайдену швидкість ділять на відстань даної точки до миттєвої осі обертання, положення якої часто визначають з механічної умови задачі і отримують кутову швидкість тіла.
Якщо нерухому точку  вибрати за початок нерухомої і рухомої систем координат (див. рис. 133) і координати точки, швидкість якої визначається, позначити відповідно через (
вибрати за початок нерухомої і рухомої систем координат (див. рис. 133) і координати точки, швидкість якої визначається, позначити відповідно через ( ) – в нерухомій системі координат, (
) – в нерухомій системі координат, ( ) – в рухомій, то на основі формул для проекцій векторного добутку на координатні осі з формули (а) отримаємо
) – в рухомій, то на основі формул для проекцій векторного добутку на координатні осі з формули (а) отримаємо
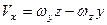 ;
;
 ; (2.82)
; (2.82)
 ;
;
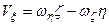 ;
;
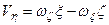 ; (2.83)
; (2.83)
 .
.
Формули (2.82) визначають проекції вектора швидкості точки тіла, яке здійснює сферичний рух, на нерухомі осі координат, а формули (2.83) – проекції на рухомі осі координат. В даних формулах  ,
,  ,
, 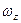 ,
,  ,
,  ,
,  – проекції вектора кутової швидкості на відповідні осі координат.
– проекції вектора кутової швидкості на відповідні осі координат.
Якщо точка знаходиться на миттєвій осі обертання, то швидкість її дорівнює нулеві (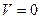 ), а це означає, що дорівнюють нулеві проекції вектора швидкості на координатні осі. З формул (2.82) отримаємо рівняння миттєвої осі обертання в нерухомій системі координат
), а це означає, що дорівнюють нулеві проекції вектора швидкості на координатні осі. З формул (2.82) отримаємо рівняння миттєвої осі обертання в нерухомій системі координат
 ;
;
 ;
;
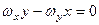 ,
,
або
 . (2.84)
. (2.84)
Отримане рівняння для конкретного моменту часу є рівнянням миттєвої осі обертання в нерухомій системі координат.
Якщо величини, які входять в рівняння (2.84), розглядати як функцію часу, то дане рівняння є параметричним рівнянням нерухомого аксоїда. Аналогічно з формул (2.83) можна отримати параметричне рівняння рухомого аксоїда
 . (2.85)
. (2.85)
Пришвидшення точок твердого тіла, яке обертається навколо нерухомої точки
Розглянемо тверде тіло, яке обертається навколо нерухомої точки  , і візьмемо в ньому яку-небудь точку
, і візьмемо в ньому яку-небудь точку  (рис. 141). На цьому ж рисунку зображено:
(рис. 141). На цьому ж рисунку зображено:
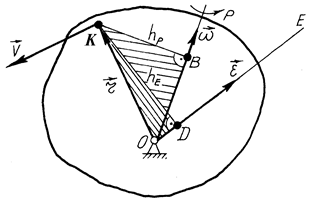
Рис. 141
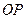 – миттєву вісь обертання;
– миттєву вісь обертання;
 – миттєву лінію кутового пришвидшення;
– миттєву лінію кутового пришвидшення;
 – вектори відповідно кутової швидкості і кутового пришвидшення тіла в деякий момент часу;
– вектори відповідно кутової швидкості і кутового пришвидшення тіла в деякий момент часу;
 – відстань точки
– відстань точки  до миттєвої осі обертання;
до миттєвої осі обертання;
 – відстань даної точки до лінії кутового пришвидшення;
– відстань даної точки до лінії кутового пришвидшення;
 – вектор швидкості точки
– вектор швидкості точки  , який згідно з попереднім визначається за формулою
, який згідно з попереднім визначається за формулою
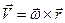 .
.
За визначенням пришвидшення (пришвидшення – це перша похідна за часом від вектора швидкості) і, враховуючи правило диференціювання векторного добутку, матимемо
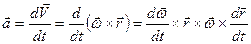 .
.
Враховуючи, що  , а
, а  , отримаємо
, отримаємо
 . (а)
. (а)
Таким чином, шукане пришвидшення складається з двох доданків. Знайдемо величину і напрями цих доданків і введемо відповідні позначення.
Векторний добуток  називається обертальним пришвидшенням і позначається
називається обертальним пришвидшенням і позначається 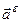 . Отже,
. Отже,
 . (2.86)
. (2.86)
Його величина, згідно з правилами обчислення векторного добутку, дорівнює


 .
.
З (рис. 141) маємо
(рис. 141) маємо  .
.
Отже
 . (2.87)
. (2.87)
Обертальне пришвидшення точки тіла, яке рухається навколо нерухомої точки, чисельно дорівнює добутку кутового пришвидшення тіла на відстань даної точки до лінії кутового пришвидшення.
Вектор обертального пришвидшення 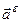 за визначенням векторного добутку перпендикулярний до площини, яка проходить через вектори
за визначенням векторного добутку перпендикулярний до площини, яка проходить через вектори 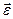 і
і 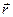 , або, що те саме, – до площини, яка проходить через вектор кутового пришвидшення
, або, що те саме, – до площини, яка проходить через вектор кутового пришвидшення 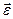 і точку
і точку  (див. рис. 141) і напрямлений в бік, звідки поворот на кут, менший 180°, першого вектора
(див. рис. 141) і напрямлений в бік, звідки поворот на кут, менший 180°, першого вектора 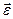 до другого –
до другого – 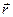 , щоб їх сумістити, видно проти руху годинникової стрілки.
, щоб їх сумістити, видно проти руху годинникової стрілки.
Треба зазначити, що в даному випадку обертальне пришвидшення 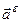 не можна називати дотичним, бо воно загалом не співпадає з напрямом вектора швидкості
не можна називати дотичним, бо воно загалом не співпадає з напрямом вектора швидкості  . І дійсно, швид-кість
. І дійсно, швид-кість 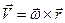 напрямлена перпендикулярно до площини, яка утворена векторами
напрямлена перпендикулярно до площини, яка утворена векторами  і
і 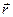 , а
, а 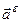 напрямлено перпендикулярно до площини, яка утворена векторами
напрямлено перпендикулярно до площини, яка утворена векторами 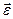 і
і 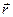 . Вектори
. Вектори  і
і 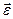 мають різні напрями, і загалом дані площини не співпадають.
мають різні напрями, і загалом дані площини не співпадають.
Векторний добуток 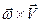 називається доосьовим пришвидшенням і позначається
називається доосьовим пришвидшенням і позначається  , тобто:
, тобто:
 . (2.88)
. (2.88)
Його величина

 .
.
Оскільки вектори  і
і  взаємно перпендикулярні (див. попередній параграф) і
взаємно перпендикулярні (див. попередній параграф) і 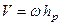 , отримаємо
, отримаємо
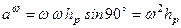 .
.
Отже,
Доосьове пришвидшення точки тіла, яке здійснює сферичний рух, чисельно дорівнює добутку квадрата кутової швидкості тіла на відстань даної точки до миттєвої осі обертання
 . (2.89)
. (2.89)
Щодо напряму цього пришвидшення, то воно перпендикулярне до площини побудованого на векторах  і
і  прямокутника (рис. 142), де для побудови цього прямокутника вектор
прямокутника (рис. 142), де для побудови цього прямокутника вектор  умовно зображено в точці
умовно зображено в точці  . Перпендикуляром до цієї площини є відрізок
. Перпендикуляром до цієї площини є відрізок  , тобто перпендикуляр, який опущений з точки
, тобто перпендикуляр, який опущений з точки  на миттєву вісь обертання. Отже, вектор доосьового пришвидшення напрямлений вздовж перпендикуляра, опущеного з точки, пришвидшення якої визначається, на миттєву вісь обертання. За визначенням векторного добутку легко переконатись, що цей вектор буде напрямлений до миттєвої осі обертання. Ось чому він називається доосьовим. Враховуючи введені позначення, формула (а) набуває вигляду
на миттєву вісь обертання. Отже, вектор доосьового пришвидшення напрямлений вздовж перпендикуляра, опущеного з точки, пришвидшення якої визначається, на миттєву вісь обертання. За визначенням векторного добутку легко переконатись, що цей вектор буде напрямлений до миттєвої осі обертання. Ось чому він називається доосьовим. Враховуючи введені позначення, формула (а) набуває вигляду
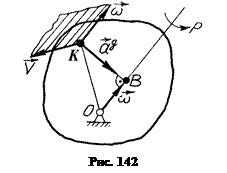
 , (2.90)
, (2.90)
тобто,
Пришвидшення точки твердого тіла, яке обертається навколо нерухомої точки, дорівнює геометри-чній сумі її обертального і доосьового пришвидшень.
Цю тезу часто називають теоремою Рівальса.
Загалом вектори обертального і доосьового пришвидшень не перпендикулярні один до одного, а тому величину пришвидшення 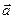 вираховують як діагональ паралелограма, який будується на векторах
вираховують як діагональ паралелограма, який будується на векторах  і
і 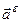 (рис. 143) за формулою
(рис. 143) за формулою

 . (2.91)
. (2.91)
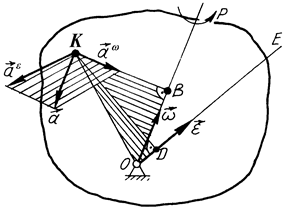
Рис. 143
Питання для самоконтролю
1. Скільки ступенів вільності має тверде тіло, що обертається навколо нерухомої точки?
2. Чому обертання твердого тіла навколо нерухомої точки називають сферичним рухом?
3. Запишіть рівняння обертання твердого тіла навколо нерухомої точки.
4. Що називається кутовою швидкістю твердого тіла, яке обертається навколо нерухомої точки?
5. Сформулюйте теорему Ейлера-Даламбера.
6. Як зображується вектор кутової швидкості твердого тіла, що обертається навколо нерухомої точки?
7. Запишіть формули, за допомогою яких можна визначити вектор кутового пришвидшення тіла, що обертається навколо нерухомої точки.
8. Чому в кожний момент часу вектор швидкості точки тіла, котре здійснює сферичний рух, можна визначити за формулою Ейлера?
9. Запишіть формулу Ейлера, яка визначає вектор швидкості точки тіла в обертальному русі.
10. За якою формулою визначається величина швидкості точки тіла, котре здійснює сферичний рух?
11. Запишіть формули, які визначають проекції на нерухомі осі координат вектора швидкості точки тіла, яке здійснює сферичний рух.
12. Сформулюйте теорему Рівальса.
13. За якою формулою визначається величина доосьового пришвидшення?
14. За якою формулою визначається величина обертального пришвидшення точки тіла в сферичному русі?
15. Тіло обертається навколо нерухомої точки. В даний момент часу проекції вектора кутової швидкості на нерухомі осі координат мають значення: 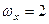 с–1,
с–1, 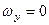 ,
, 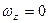 . Що в даний момент часу є миттєвою віссю обертання тіла?
. Що в даний момент часу є миттєвою віссю обертання тіла?
16. В деякий момент часу тіло, яке обертається навколо нерухомої точки, має кутову швидкість 2 с–1, кутове пришвид-шення 3 с–2. Вектор кутової швидкості в даний момент часу напрямлений вздовж осі абсцис, а вектор кутового пришвидшення – вздовж осі ординат. Знайти величину швидкості точки М (0,4; 0,3; 0). Координати точок задані в метрах. Початок системи координат знаходиться в нерухомій точці тіла.
17. За умовою питання №16 визначити доосьове пришвидшення точки М.
18. За умовою питання №16 знайти величину обертального пришвидшення точки М.
19. За умовою питання №16 вказати напрям вектора швидкості точки М.
20. За умовою питання №16 вказати напрям вектора доосьового пришвидшення точки М.
21. За умовою питання №16 вказати напрям вектора обертального пришвидшення точки М.
Рух вільного твердого тіла
Рис. 144
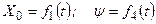 ;
;
 ; (2.92)
; (2.92)
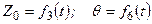
визначатиме рівняння руху вільного твердого тіла, бо за допомогою цих рівнянь можна визначити положення тіла в будь-який момент часу.
Звернемо увагу на те, що рух вільного твердого тіла є складним. Він складається з поступального руху разом з деякою точкою, яка називається, як і в плоскопаралельному русі полюсом, і обертання навколо даної точки. І дійсно, в частковому випадку, коли
 ;
;
 ; (2.92)
; (2.92)
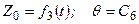 ,
,
де  – деякі константи, отримаємо поступальний рух твердого тіла. А у випадку, коли
– деякі константи, отримаємо поступальний рух твердого тіла. А у випадку, коли
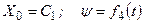 ;
;
 ;
;
 ,
,
тіло буде обертатись навколо нерухомої точки.
Оскільки за полюс можна взяти будь-яку точку твердого тіла, то, вибираючи різні точки тіла за полюс, отримаємо безліч розкладень руху вільного тіла на поступальну і обертальну частини. Легко довести, що поступальна частина руху залежить від вибору полюса, а обертальна – не залежить. Це саме було отримано для плоскопаралельного руху (див. § 46.2).
Для обертального руху твердого тіла навколо точки  згідно з попереднім параграфом в кожний момент часу існує миттєва вісь обертання, яка проходить через точку
згідно з попереднім параграфом в кожний момент часу існує миттєва вісь обертання, яка проходить через точку  . Отже, в кожний момент часу рух вільного тіла можна розглядати, як сукупність двох рухів: поступального разом з деякою точкою і обертального навколо деякої миттєвої осі, яка проходить через дану точку.
. Отже, в кожний момент часу рух вільного тіла можна розглядати, як сукупність двох рухів: поступального разом з деякою точкою і обертального навколо деякої миттєвої осі, яка проходить через дану точку.
Перейдемо до визначення швидкостей точок вільного тіла. Швидкість довільної точки  дорівнює похідній за часом від радіуса-вектора
дорівнює похідній за часом від радіуса-вектора  , який визначає її положення в нерухомій системі відліку. На підставі рис. 144 маємо
, який визначає її положення в нерухомій системі відліку. На підставі рис. 144 маємо
 .
.
Отже,
 .
.
Оскільки 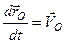 – швидкість точки
– швидкість точки  , а похідна
, а похідна  є швидкість точки
є швидкість точки  відносно точки
відносно точки  –
–  , то отримуємо
, то отримуємо
 . (2.93)
. (2.93)
Отриману формулу можна прочитати так:
Швидкість будь-якої точки вільного тіла дорівнює геометричній сумі швидкості довільно вибраного полюса і швидкості даної точки в обертальному русі тіла навколо полюса.
Продиференціювавши векторну рівність (2.93) за часом

і знаючи, що перша похідна за часом від вектора лінійної швидкості визначає вектор відповідного лінійного пришвидшення, отримаємо
 , (2.94)
, (2.94)
тобто:
Пришвидшення будь-якої точки вільного тіла дорів-нює геометричній сумі пришвидшення полюса і при-швидшення даної точки в обертальному русі тіла навколо полюса.
Таким чином, отримано формули, які дають змогу обчислювати швидкість (формула 2.93) і пришвидшення (формула 2.94) будь-якої точки вільного тіла. В даних формулах вектори  і
і  визначається так, як було вказано в попередньому параграфі.
визначається так, як було вказано в попередньому параграфі.
Питання для самоконтролю
1. Яке тверде тіло називається вільним?
2. Скільки ступенів вільності має вільне тверде тіло?
3. Скільки незалежних параметрів необхідно для однозначного визначення положення вільного тіла в просторі?
4. Запишіть рівняння руху вільного твердого тіла.
5. Що називається полюсом вільного твердого тіла?
6. З яких рухів складається рух вільного твердого тіла?
7. Як залежать складові рухи вільного твердого тіла від вибору полюса?
8. Запишіть і прочитайте формулу, за допомогою якої визначається швидкість точки вільного тіла.
9. Запишіть і прочитайте формулу, за допомогою якої визначається пришвидшення точки вільного тіла.
10. В деякий момент часу пришвидшення точки  вільного тіла визначається виразом
вільного тіла визначається виразом  . В цей момент часу кутова швидкість тіла
. В цей момент часу кутова швидкість тіла  , кутове пришвидшення
, кутове пришвидшення  . Знайти пришвидшення точки
. Знайти пришвидшення точки  тіла, якщо
тіла, якщо 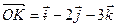 .
.
11. Рух вільного тіла описується рівняннями  ,
, 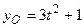 ,
,  ,
,  ,
,  ,
,  . Знайти в момент часу
. Знайти в момент часу  с швидкість полюса, якщо
с швидкість полюса, якщо  м,
м,  рад.
рад.
12. Тіло вільно рухається в просторі згідно з рівняннями 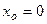 ,
,  м,
м,  м,
м,  рад,
рад,  рад,
рад, 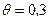 рад. Визначить модуль кутової швидкості тіла в момент часу
рад. Визначить модуль кутової швидкості тіла в момент часу  с.
с.
13. Знайти проекцію на нерухому вісь абсцис швидкості точки  вільного тіла, якщо її радіус-вектор відносно полюса
вільного тіла, якщо її радіус-вектор відносно полюса  , миттєва кутова швидкість
, миттєва кутова швидкість  , а рівняння руху полюса
, а рівняння руху полюса  ,
,  ,
,  . Всі величини в системі СІ.
. Всі величини в системі СІ.
Синтез рухів
Тут для розгляду складного руху твердого тіла застосовуємо метод синтезу, тобто складний рух твердого тіла отримаємо способом складання його найпростіших рухів. Основною метою даного параграфа є визначення результуючого руху твердого тіла, яке здійснює одночасно два або декілька простих рухів і отримання залежностей між кінематичними характеристиками результуючого і складових рухів.
Складання поступальних рухів твердого тіла
Для визначення результуючого руху розглянемо тверде тіло, яке рухається поступально з швидкістю відносно рухомої системи координат , яка в свою… (а) За переносний рух тіла приймаємо його рух разом з рухомою системою координат . Оскільки рухома система координат…При складанні двох поступальних рухів твердого тіла результуючий рух тіла є поступальним зі швидкістю, яка дорівнює геометричній сумі швидкостей складових рухів
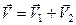 , (2.95)
, (2.95)
У випадку 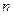 поступальних рухів, користуючись принципом незалежності рухів (див. курс фізики) і застосовуючи послідовно попередні міркування, отримаємо, що результуючий рух також буде поступальним, а його швидкість буде дорівнювати геометричній сумі швидкостей складових рухів, тобто
поступальних рухів, користуючись принципом незалежності рухів (див. курс фізики) і застосовуючи послідовно попередні міркування, отримаємо, що результуючий рух також буде поступальним, а його швидкість буде дорівнювати геометричній сумі швидкостей складових рухів, тобто
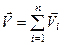 . (2.96)
. (2.96)
Якщо швидкості всіх точок тіла геометрично рівні тільки в деякий момент часу, то рух в такому випадку називається миттєво-поступальним. Миттєво-поступальний рух твердого тіла відрізняється тим, що в даному русі геометрично рівні тільки швидкості всіх точок тіла, а пришвидшення різні, тобто

але

тоді як при поступальному русі тіла швидкості і пришвидшення всіх його точок геометрично рівні.
Складання поступального і обертального рухів твердого тіла
Розглянемо складний рух твердого тіла, який складається з поступального і обертального навколо деякої осі. Тут можуть зустрітись такі випадки: вектор швидкості поступального руху є: а) перпендикулярним до осі обертання; б) паралельним до осі обертання; в) утворює з віссю обертання довільний кут. Розглянемо окремо кожний з цих випадків.
А) Швидкість поступального руху перпендикулярна до осі обертання
Прикладом такого руху є рух автомобільних коліс, які рухаються поступально разом з автомобілем і одночасно обертаються навколо відповідних осей, до того ж в кожний момент часу швидкість поступального руху перпендикулярна до осі обертання колеса.
Припустимо, що тіло  обертається з кутовою швидкістю
обертається з кутовою швидкістю  навколо осі
навколо осі  , яка жорстко скріплена з іншим тілом (наприклад, з площиною
, яка жорстко скріплена з іншим тілом (наприклад, з площиною 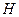 ), яке рухається поступально зі швидкістю
), яке рухається поступально зі швидкістю  , перпендикулярною до осі
, перпендикулярною до осі  (рис. 146). Для визначення результуючого руху на осі
(рис. 146). Для визначення результуючого руху на осі  візьмемо довільну точку
візьмемо довільну точку  , через яку проведемо осі
, через яку проведемо осі  і
і  , причому вісь
, причому вісь  проведемо паралельно до вектора
проведемо паралельно до вектора  . На осі
. На осі  візьмемо точку
візьмемо точку 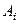 на відстані
на відстані
 (а)
(а)
і визначимо її швидкість. Тіло  здійснює складний рух, отже кожна його точка здійснює складний рух, а це означає, що швидкість точки
здійснює складний рух, отже кожна його точка здійснює складний рух, а це означає, що швидкість точки 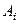 можна обчислити за формулою
можна обчислити за формулою
 . (б)
. (б)
За переносний рух приймемо поступальний рух твердого тіла, тоді переносна швидкість кожної точки тіла буде дорівнювати  , тобто:
, тобто:
 . (в)
. (в)
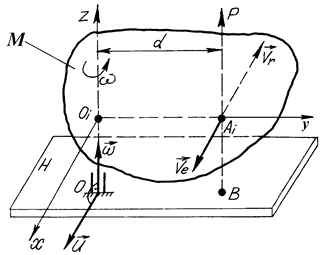
Рис. 146
За відносний рух приймемо обертання твердого тіла навколо осі  , тоді величина відносної швидкості кожної точки тіла буде дорівнювати добутку кутової швидкості на відстань даної точки до осі обертання. Для точки
, тоді величина відносної швидкості кожної точки тіла буде дорівнювати добутку кутової швидкості на відстань даної точки до осі обертання. Для точки 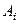 , враховуючи співвідношення (а), отримаємо
, враховуючи співвідношення (а), отримаємо
 . (г)
. (г)
Вектор відносної швидкості як вектор обертальної швидкості буде перпендикулярним до відповідного радіуса. Для точки 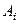
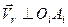 і напрямлений в бік обертання, як вказано на рис. 146.
і напрямлений в бік обертання, як вказано на рис. 146.
Підставляючи (в) і (г) у формулу (б) і враховуючи, що вектори 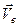 і
і 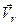 напрямлені по одній прямій в протилежні боки, отримаємо
напрямлені по одній прямій в протилежні боки, отримаємо
 ,
,
тобто абсолютна швидкість точки  в даний момент часу дорівнює нулеві.
в даний момент часу дорівнює нулеві.
Якщо через точку  паралельно до осі
паралельно до осі  провести вісь
провести вісь  і врахувати, що на осі
і врахувати, що на осі  точку
точку  вибрано довільно (отже, і точка
вибрано довільно (отже, і точка  є довільною точкою осі
є довільною точкою осі  ), то можна зробити такий висновок: вісь
), то можна зробити такий висновок: вісь  є геометричне місце точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла в даний момент часу є обертальним.
є геометричне місце точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла в даний момент часу є обертальним.
Таким чином,
При складанні поступального і обертального рухів твердого тіла у випадку, коли швидкість поступального руху перпендикулярна до осі обертання, результуючий рух тіла в кожний момент часу є обертальним навколо миттєвої осі обертання, паралельної до осі обертання складового руху, і знаходиться від неї на відстані d, яка визначається за формулою
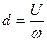 . (2.97)
. (2.97)
Відрізок 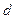 відкладається вздовж перпендикуляра до площини, яка проходить через вектори
відкладається вздовж перпендикуляра до площини, яка проходить через вектори  і
і  в бік, звідки поворот вектора
в бік, звідки поворот вектора  до
до  на кут
на кут 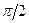 видно проти руху годинникової стрілки.
видно проти руху годинникової стрілки.
Позначимо кутову швидкість результуючого (абсолютною) руху  і визначимо її. Для цього за формулою
і визначимо її. Для цього за формулою
 (д)
(д)
визначимо абсолютну швидкість точки  . Кожний з векторів які входять в рівність (д), легко обчислити:
. Кожний з векторів які входять в рівність (д), легко обчислити:
 , адже абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі
, адже абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі  ;
;
 , бо переносний рух, як було прийнято, є поступальним зі швидкістю
, бо переносний рух, як було прийнято, є поступальним зі швидкістю  ;
;
 , точка
, точка  знаходиться на осі відносного обертання.
знаходиться на осі відносного обертання.
Враховуючи все це, з рівності (д) отримаємо
 .
.
Звідки, враховуючи формулу (а), матимемо
 ,
,
Кутова швидкість результуючого (абсолютного) руху дорівнює кутовій швидкості складового обертання.
На закінчення звернемо увагу на те, що цей вид руху тіла є не що інше як плоскопаралельний рух, який, як відомо, визначається рухом плоскої фігури в її площині. Саму плоску фігуру отримаємо шляхом перетину тіла площиною, перпендикулярною до осі  . Миттєвий центр швидкостей, навколо якого плоска фігура в даний момент часу здійснює обертальний рух, буде знаходитися в точці її перетину з миттєвою віссю (
. Миттєвий центр швидкостей, навколо якого плоска фігура в даний момент часу здійснює обертальний рух, буде знаходитися в точці її перетину з миттєвою віссю ( ) обертання тіла.
) обертання тіла.
Б) Швидкість поступального руху паралельна осі обертання
 Прикладом такого руху є рух свердла свердлильного верстата, рух гайки при закручуванні її на болт, рух гвинта при польоті літака і т.п.
Прикладом такого руху є рух свердла свердлильного верстата, рух гайки при закручуванні її на болт, рух гвинта при польоті літака і т.п.
На рис. 147 зображено тіло  , яке обертається навколо осі
, яке обертається навколо осі  з кутовою швидкістю
з кутовою швидкістю  і одночасно рухається зі швидкістю
і одночасно рухається зі швидкістю  , причому
, причому 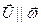 . Швидкість будь-якої точки
. Швидкість будь-якої точки  , яка, як і все тіло, здійснює складний рух, буде визначатись формулою
, яка, як і все тіло, здійснює складний рух, буде визначатись формулою
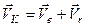 . (а)
. (а)
Прийнявши за переносний рух поступальний рух твердого тіла, а за відносний – його обертання навколо осі  , матимемо
, матимемо
 ;
;  ,
,
і формула (а) набуває вигляду
 . (б)
. (б)
Таким чином, абсолютна швидкість точки може бути розкладена на дві складові: одна з них 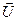 паралельна до осі
паралельна до осі  ; інша
; інша  знаходиться в площині, яка перпендикулярна до осі, до того ж вона перпендикулярна до площини, яка проходить через вісь
знаходиться в площині, яка перпендикулярна до осі, до того ж вона перпендикулярна до площини, яка проходить через вісь  і точку
і точку  (рис. 147). Звідси можна зробити висновок, що точки тіла рухаються по бокових поверхнях циліндрів з віссю
(рис. 147). Звідси можна зробити висновок, що точки тіла рухаються по бокових поверхнях циліндрів з віссю  і радіусом
і радіусом 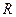 , де
, де 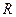 – відстань точки до осі
– відстань точки до осі  , а траєкторією їх є гвинтові лінії.
, а траєкторією їх є гвинтові лінії.
Отже,
При складанні поступального і обертального рухів твердого тіла у випадку, коли швидкість поступального руху паралельна осі обертання, результуючий (абсолютний) рух тіла є гвинтовим, бо його точки описують гвинтові лінії.
Однієї з основних геометричних характеристик гвинта є його крок.
Кроком гвинта називається відстань, яку проходить точка осі гвинта за один оберт тіла.
Точки осі гвинта рухаються зі швидкістю  . Припустивши, що
. Припустивши, що  ,
,  , отримаємо формулу, яка визначає крок (
, отримаємо формулу, яка визначає крок ( ) кінематичного гвинта
) кінематичного гвинта
 . (2.98)
. (2.98)
Відношення
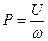 (2.99)
(2.99)
називається параметром кінематичного гвинта.
Якщо швидкості  і
і  змінні, то, природно, параметри кінематичного гвинта будуть змінними.
змінні, то, природно, параметри кінематичного гвинта будуть змінними.
В) Швидкість поступального руху утворює довільний кут з віссю обертання
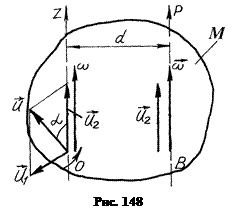 Нехай тіло
Нехай тіло  обертається навколо осі
обертається навколо осі  з кутовою швидкістю
з кутовою швидкістю  і одночасно рухається поступально з швидкістю
і одночасно рухається поступально з швидкістю  , яка утворює довільний кут
, яка утворює довільний кут 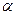 з віссю обертання (рис. 148). Для визначення результуючого руху вектор швидкості
з віссю обертання (рис. 148). Для визначення результуючого руху вектор швидкості  розкладено на дві складові
розкладено на дві складові
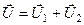 ,
,
одна з яких 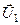 перпендикулярна до осі
перпендикулярна до осі  , причому
, причому
 ,
,
інша  – паралельна до осі
– паралельна до осі  .
.
 .
.
Застосовуючи принцип незалежності рухів і склавши поступальний рух з швидкістю  з обертанням навколо осі
з обертанням навколо осі  , отримаємо, згідно з пунктом (а), миттєвий обертальний рух навколо миттєвої осі
, отримаємо, згідно з пунктом (а), миттєвий обертальний рух навколо миттєвої осі  , яка паралельна до осі
, яка паралельна до осі  з кутовою швидкістю
з кутовою швидкістю  . Математично це можна записати так:
. Математично це можна записати так:
 .
.
Відстань до миттєвої осі обертання можна визначити за формулою (2.97)
 .
.
Тепер, якщо скласти миттєвий обертальний рух навколо осі  з поступальним рухом з швидкістю
з поступальним рухом з швидкістю  , яка паралельна осі
, яка паралельна осі  , то, згідно з пунктом б), отримаємо в кожний момент часу гвинтовий рух, тобто
, то, згідно з пунктом б), отримаємо в кожний момент часу гвинтовий рух, тобто  (миттєвий гвинтовий рух навколо
(миттєвий гвинтовий рух навколо  ).
).
Крок гвинта в даному випадку буде визначатись формулою
 . (2.100)
. (2.100)
Складання обертань навколо осей, що перетинаються
Для визначення результуючого руху розглянемо тверде тіло (рис. 150), яке одночасно обертається навколо двох осей: навколо осі з кутовою швидкістю і… З точки перетину осей вздовж відповідних осей відкладемо вектори і і на цих… . (а)Кутова швидкість результуючого (абсолютного) обертання дорівнює геометричній сумі кутових швидкостей складових рухів.
Звернемо увагу на те, що геометрично визначаючи кутову швидкість абсолютного обертання за формулою (2.101), знаходимо не тільки її величину і напрям, а й вказуємо положення миттєвої осі абсолютного обертання (див. рис. 150).
Очевидно, базуючись на принципі незалежності рухів, доведене вище можна узагальнити на рух твердого тіла, який складається з трьох і більше миттєвих обертань навколо осей, що перетинаються в одній точці, тобто:
Сукупність обертань тіла навколо осей, що перетинаються в одній точці, еквівалентна одному обер-танню з кутовою швидкістю, яка дорівнює геометричній сумі кутових швидкостей складових рухів
 . (2.102)
. (2.102)
Отримане обґрунтовує векторну природу кутової швидкості твердого тіла , оскільки кутові швидкості твердого тіла підпорядковуються правилу векторного складання. Припущення, які були зроблені в §43.4 про кутову швидкість як про ковзний вектор, отримало тут повне обґрунтування. До того ж воно підтверджує теорему Ейлера–Даламбера (див § 47.2), згідно з якою сферичний рух тіла, який є сукупністю трьох обертань, в кожний момент часу можна розглядати як обертання навколо миттєвої осі з кутовою швидкістю  , яку, якщо задані рівняння обертання твердого тіла навколо нерухомої точки (рів. 2.77) згідно з (2.102), можна визначити за формулою
, яку, якщо задані рівняння обертання твердого тіла навколо нерухомої точки (рів. 2.77) згідно з (2.102), можна визначити за формулою
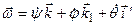 , (2.103)
, (2.103)
в якій 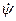 ,
,  ,
,  – миттєві алгебраїчні кутові швидкості тіла відповідно навколо осей
– миттєві алгебраїчні кутові швидкості тіла відповідно навколо осей  ,
,  ,
, 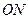 ;
;  ,
,  ,
,  – орти відповідних осей (див. рис 134).
– орти відповідних осей (див. рис 134).
Складання обертань навколо паралельних осей
При складанні обертань навколо паралельних осей можуть бути такі випадки: а) обертання напрямлені в один бік; б) обертання напрямлені в протилежні…Рис. 151
Розглянемо окремо кожний з цих випадків.
А) Обертання напрямлені в один бік
Нехай тверде тіло  обертається навколо осі
обертається навколо осі 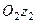 з кутовою швидкістю
з кутовою швидкістю  , а сама вісь
, а сама вісь 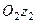 обертається навколо паралельної їй осі
обертається навколо паралельної їй осі 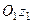 з кутовою швидкістю
з кутовою швидкістю 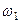 (рис. 152). Обертання навколо осей
(рис. 152). Обертання навколо осей 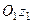 і
і 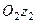 , як видно з цього рисунка, напрямлені в один бік. Для визначення результуючого руху твердого тіла
, як видно з цього рисунка, напрямлені в один бік. Для визначення результуючого руху твердого тіла  , яке при заданій постановці задачі одночасно обертається навколо двох паралельних осей (осі
, яке при заданій постановці задачі одночасно обертається навколо двох паралельних осей (осі 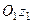 і
і 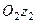 ), з довільної точки
), з довільної точки 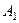 осі
осі 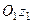 перпендикулярно до осей обертання проведемо відрізок прямої
перпендикулярно до осей обертання проведемо відрізок прямої 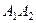 . На цьому відрізку беремо точку
. На цьому відрізку беремо точку  , яка ділить даний відрізок у співвідношенні
, яка ділить даний відрізок у співвідношенні
 (а)
(а)
і визначимо її швидкість. Точка  здійснює складний рух, бо належить тілу
здійснює складний рух, бо належить тілу  , яке здійснює складний рух, отже її швидкість можна визначити за теоремою про складання швидкостей
, яке здійснює складний рух, отже її швидкість можна визначити за теоремою про складання швидкостей
 . (б)
. (б)
Якщо обертання тіла навколо осі 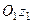 прийняти за переносний рух, а навколо осі
прийняти за переносний рух, а навколо осі 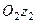 – за відносний, то матимемо:
– за відносний, то матимемо:

Рис. 152
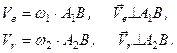 (в)
(в)
Вектори даних швидкостей напрямлені в боки відповідних обертань і, як видно з рис. 152, вони є протилежними, а це означає, що векторна сума (б) перетворюється в алгебраїчну різницю
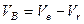
і, враховуючи (в) і (а), отримаємо
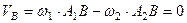 .
.
Абсолютна швидкість точки  в даний момент часу дорівнює нулеві.
в даний момент часу дорівнює нулеві.
Якщо через точку  паралельно заданим осям
паралельно заданим осям  і
і  провести вісь
провести вісь  і врахувати, що на осі
і врахувати, що на осі 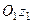 точку
точку 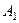 вибрано довільно (отже, і точка
вибрано довільно (отже, і точка  є довільною точкою осі
є довільною точкою осі 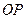 ), то можна зробити такий висновок: вісь
), то можна зробити такий висновок: вісь 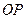 є геометричним місцем точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання тіла, а це означає, що результуючий рух твердого тіла є обертальним.
є геометричним місцем точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання тіла, а це означає, що результуючий рух твердого тіла є обертальним.
Таким чином,
При складанні обертальних рухів твердого тіла на-вколо двох паралельних осей у випадку, коли обертання напрямлені в один бік, результуючий (абсолютний) рух є обертальним в той самий бік навколо миттєвої осі обертання, яка розміщена в площині, що проходить через осі обертань складових рухів, паралельно до них, і ділить відстань між ними внутрішнім чином на відрізки, котрі обернено пропорційні кутовим швидкостям складових рухів
 . (2.104)
. (2.104)
Позначимо кутову швидкість результуючого (абсолютного) обертання  і обчислимо її. Для цього за теоремою про складання швидкостей знайдемо швидкість точки
і обчислимо її. Для цього за теоремою про складання швидкостей знайдемо швидкість точки 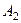 тіла
тіла  (рис. 152)
(рис. 152)
 . (г)
. (г)
В записаній рівності:
 , бо абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі обертання
, бо абсолютний рух, як було тільки що доведено, є обертальним навколо миттєвої осі обертання 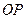 ;
;
 , бо переносний рух, як було прийнято вище, є обертальним навколо осі
, бо переносний рух, як було прийнято вище, є обертальним навколо осі 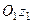 (рис. 152);
(рис. 152);
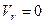 , точка
, точка 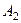 знаходиться на осі відносного обертання
знаходиться на осі відносного обертання 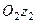 .
.
Враховуючи це, рівність (г) набуває вигляду
 .
.
Звідси матимемо
 .
.
Якщо замість відношення  підставити його значення з (а), то остаточно отримуємо
підставити його значення з (а), то остаточно отримуємо
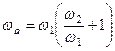 ,
,
тобто:
 . (2.105)
. (2.105)
Кутова швидкість абсолютного обертання дорівнює сумі кутових швидкостей складових рухів.
Б) Обертання напрямлені в протилежні боки і здійсню-ються з різними за величиною кутовими швидкостями
Нехай тверде тіло  обертається навколо осі
обертається навколо осі 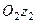 з кутовою швидкістю
з кутовою швидкістю  , а сама вісь
, а сама вісь 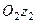 обертається навколо паралельної до неї осі
обертається навколо паралельної до неї осі 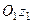 з кутовою швидкістю
з кутовою швидкістю 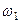 (рис. 153). Обертання навколо осей
(рис. 153). Обертання навколо осей 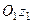 і
і 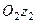 , як видно з цього рисунка, напрямлені в протилежні боки. Припустимо, що
, як видно з цього рисунка, напрямлені в протилежні боки. Припустимо, що  , і нехай
, і нехай  .
.

Рис. 153
Для визначення результуючого руху твердого тіла  , яке при заданій постановці задачі одночасно обертається нав-коло двох паралельних осей в протилежні боки, як і в попередньому випадку, з довільної точки
, яке при заданій постановці задачі одночасно обертається нав-коло двох паралельних осей в протилежні боки, як і в попередньому випадку, з довільної точки 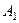 осі
осі 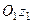 перпендикулярно до осей обертання проведемо відрізок
перпендикулярно до осей обертання проведемо відрізок 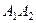 . На продовженні цього відрізка (продовження проводимо за вісь, навколо якої тіло обертається з більшою кутовою швидкістю; в даному випадку це вісь
. На продовженні цього відрізка (продовження проводимо за вісь, навколо якої тіло обертається з більшою кутовою швидкістю; в даному випадку це вісь 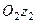 ) беремо точку
) беремо точку  , положення якої визначається співвідношенням
, положення якої визначається співвідношенням
 , (а)
, (а)
і за теоремою про складання швидкостей визначимо її швидкість
 . (б)
. (б)
Якщо обертання тіла навколо осі 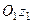 прийняти за переносний рух, а навколо осі
прийняти за переносний рух, а навколо осі 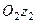 – за відносний, то матимемо
– за відносний, то матимемо
 (в)
(в)
Вектори 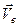 і
і 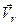 напрямлені в боки відповідних обертань, як видно з рис. 153, вони є протилежними, а це означає, що векторна сума (б) перетворюється в алгебраїчну різницю
напрямлені в боки відповідних обертань, як видно з рис. 153, вони є протилежними, а це означає, що векторна сума (б) перетворюється в алгебраїчну різницю
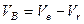 ,
,
і, враховуючи (в) і (а), отримаємо
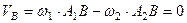 ,
,
абсолютна швидкість точки  в даний момент часу дорівнює нулеві.
в даний момент часу дорівнює нулеві.
Якщо через точку  паралельно заданим осям
паралельно заданим осям 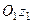 і
і 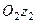 провести вісь
провести вісь 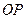 і врахувати, що на осі
і врахувати, що на осі 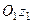 точку
точку 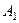 вибрано довільно (отже, і точка
вибрано довільно (отже, і точка  є довільною точкою осі
є довільною точкою осі 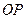 ), то можна зробити такий висновок: вісь
), то можна зробити такий висновок: вісь 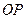 є геометричним місцем точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла є обертальним.
є геометричним місцем точок, абсолютні швидкості яких в даний момент часу дорівнюють нулеві, тобто вона є миттєвою віссю абсолютного обертання, а це означає, що результуючий рух твердого тіла є обертальним.
Таким чином,
При складанні обертальних рухів твердого тіла на-вколо двох паралельних осей у випадку, коли обертання напрямлені в протилежні боки і здійснюються з різними за величиною кутовими швидкостями, результуючий (абсолютний) рух є обертальним в бік більшої кутової швидкості навколо осі обертання, яка розміщена в площині, що проходить через осі обертань складових рухів, паралельна до них і ділить відстань між ними зовнішнім чином на відрізки, котрі обернено пропорційні кутовим швидкостям складових рухів
 . (2.106)
. (2.106)
Позначимо кутову швидкість результуючого обертання 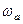 і обчислимо її. Для цього за теоремою про складання швидкостей знайдемо швидкість точки
і обчислимо її. Для цього за теоремою про складання швидкостей знайдемо швидкість точки 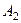 тіла
тіла  (рис. 153)
(рис. 153)
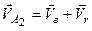 . (г)
. (г)
Оскільки переносний, відносний і абсолютний рухи твердого тіла є обертальними, то:
 , адже в абсолютному русі тіло в даний момент часу обертається навколо осі
, адже в абсолютному русі тіло в даний момент часу обертається навколо осі 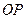 ;
;
 – за переносний рух прийнято обертання навколо осі
– за переносний рух прийнято обертання навколо осі 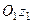 ;
;
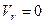 , точка
, точка 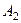 знаходиться на відносній осі обертання.
знаходиться на відносній осі обертання.
Враховуючи це, рівняння (г) набуває вигляду
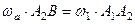 .
.
Звідси матимемо
 .
.
Якщо замість відношення  підставити його значення з (а), то отримаємо
підставити його значення з (а), то отримаємо
 ,
,
тобто:
 . (2.107)
. (2.107)
Кутова швидкість абсолютного обертання дорівнює різниці кутових швидкостей складових рухів.
в) Обертання напрямлені в протилежні боки і здій-снюються з однаковими за величиною кутовими швидкостями (пара обертань) Розглянемо тепер складний рух твердого тіла, який складається з двох обертань… Отже,Пара обертань – це сукупність двох обертань твердого тіла навколо паралельних осей з рівними за величиною, але протилежними за напрямом кутовими швидкостями.
Для визначення результуючого руху за теоремою про складання швидкостей обчислимо швидкість довільної точки  тіла, положення якої відносно точок
тіла, положення якої відносно точок 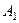 і
і 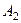 осей обертання визначається радіусами-векторами
осей обертання визначається радіусами-векторами  і
і  (рис. 154).
(рис. 154).
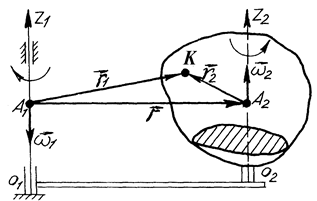
Рис. 154
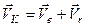 , (а)
, (а)
Оскільки переносний і відносний рухи є обертальними відповідно з кутовими швидкостями  і
і  , то вектори переносної
, то вектори переносної 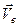 і відносної
і відносної 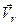 швидкостей можна обчислювати за формулою Ейлера
швидкостей можна обчислювати за формулою Ейлера
 ,
,  . (б)
. (б)
Підставивши (б) і рівність (а), отримаємо
 .
.
Якщо врахувати, що 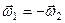 , то матимемо
, то матимемо
 .
.
Оскільки  (див. рис. 154), то
(див. рис. 154), то
 . (2.108)
. (2.108)
Оскільки швидкість точки  не залежить від її положення (вектори
не залежить від її положення (вектори 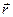 і
і  не з’єднані з точкою
не з’єднані з точкою  ), то швидкості всіх точок тіла в даний момент часу геометрично рівні між собою, а це означає, що тіло здійснює поступальний рух.
), то швидкості всіх точок тіла в даний момент часу геометрично рівні між собою, а це означає, що тіло здійснює поступальний рух.
Таким чином,
при складанні двох обертань твердого тіла навколо паралельних осей з рівними за величиною, але протилежними за напрямом кутовими швидкостями результуючий рух є поступальним,
тобто пара обертань  еквівалентна миттєвому поступальному руху з швидкістю, що дорівнює моменту пари обертань. І дійсно, за аналогією зі статикою (див. теорію пари сил §16), векторний добуток
еквівалентна миттєвому поступальному руху з швидкістю, що дорівнює моменту пари обертань. І дійсно, за аналогією зі статикою (див. теорію пари сил §16), векторний добуток  можна назвати моментом пари обертань, тобто:
можна назвати моментом пари обертань, тобто:
 . (2.109)
. (2.109)
З рівності (2.109) випливає:
1) швидкість поступального руху  перпендикулярна до площини пари і напрямлена так, що спостерігач з кінця
перпендикулярна до площини пари і напрямлена так, що спостерігач з кінця бачить вектори пари
бачить вектори пари  , що намагаються повернути площину проти руху годинникової стрілки (рис. 155);
, що намагаються повернути площину проти руху годинникової стрілки (рис. 155);

Рис. 155
2) величина цієї швидкості визначається формулою
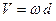 , (2.110)
, (2.110)
в якій 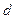 – плече пари обертання.
– плече пари обертання.
Прикладом пари обертань є рух педалі велосипеда (рис. 156). Педаль  велосипеда бере участь у двох обертаннях протилежного напряму: разом з кривошипом обертається навколо осі обертання великої зубчастої зірочки і одночасно обертається навколо власної осі (пальця
велосипеда бере участь у двох обертаннях протилежного напряму: разом з кривошипом обертається навколо осі обертання великої зубчастої зірочки і одночасно обертається навколо власної осі (пальця  кривошипа). Ці обертання здійснюються з однаковими за модулем кутовими швидкостями (
кривошипа). Ці обертання здійснюються з однаковими за модулем кутовими швидкостями ( ), адже за час одного оберту кривошипа педаль
), адже за час одного оберту кривошипа педаль  відносно кривошипа зробить також один оберт, тільки в протилежному напрямі. В результаті складання цих обертань отримується поступальний рух, підтвердженням цього є те, що педаль за час руху велосипеда нахилена під певним, до того ж сталим, кутом до полотна дороги, а це означає, що всяка пряма, проведена в педалі, залишається собі паралельною, що є характерним для поступального руху твердого тіла.
відносно кривошипа зробить також один оберт, тільки в протилежному напрямі. В результаті складання цих обертань отримується поступальний рух, підтвердженням цього є те, що педаль за час руху велосипеда нахилена під певним, до того ж сталим, кутом до полотна дороги, а це означає, що всяка пряма, проведена в педалі, залишається собі паралельною, що є характерним для поступального руху твердого тіла.

Рис. 156
Резюме. При складанні обертальних рухів як навколо осей, що перетинаються, так і навколо паралельних осей результуючий рух в кожний момент часу переважно є обертальним; тільки для пари обертань результуючий рух є поступальним.
На підставі доведеного можна розв’язувати такі задачі:
1. Складний рух твердого тіла, який складається з 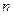 обертальних рухів навколо осей, що перетинаються в одній точці, або навколо паралельних осей, в кожний момент часу звести до одного (обертального або поступального) руху, тобто звести до канонічного вигляду.
обертальних рухів навколо осей, що перетинаються в одній точці, або навколо паралельних осей, в кожний момент часу звести до одного (обертального або поступального) руху, тобто звести до канонічного вигляду.
2. Кожний обертальний рух твердого тіла розкласти на 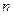 обертань навколо осей, що перетинаються в одній точці, або навколо паралельних осей.
обертань навколо осей, що перетинаються в одній точці, або навколо паралельних осей.
3. Кожний поступальний рух твердого тіла замінити парою миттєвих обертань. До того ж існує нескінченна кількість таких перетворень, але кожне з них повинно задовольняти рівність (2.109).
Питання для самоконтролю
1. Який рух твердого тіла називається складним?
2. Чи можна складанням поступальних рухів твердого тіла отримати обертальний рух тіла?
3. Тіло одночасно приймає участь у двох поступальних рухах, швидкості яких 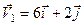 ,
,  . Знайти модуль абсолютної швидкості тіла.
. Знайти модуль абсолютної швидкості тіла.
4. Тіла 1, 2, 3 здійснюють поступальні рухи, як вказано на рисунку. Знайти в момент часу  абсолютну швидкість тіла 3, якщо
абсолютну швидкість тіла 3, якщо  ,
,  ,
,  .
.
5. В прикладі 4 визначити відносну швидкість тіла 3 відносно тіла 1.
6. Який результуючий рух тіла отримується при складанні поступального і обертального рухів у випадку, коли вектор швидкості поступального руху перпендикулярний до осі обертання?
 7. Квадрат зі стороною
7. Квадрат зі стороною
60 см рухається поступально з швидкістю  м/с і одночасно обертається навколо осі
м/с і одночасно обертається навколо осі  з кутовою швидкістю
з кутовою швидкістю  с–1. Знайдіть положення миттєвої осі абсолютного обертання квадрата, якщо
с–1. Знайдіть положення миттєвої осі абсолютного обертання квадрата, якщо 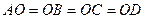 ,
,  . Яка кутова швидкість абсолютного обертання?
. Яка кутова швидкість абсолютного обертання?
8. В якому випадку при складанні простих рухів отримується гвинтовий рух?
9. Що називається кроком кінематичного гвинта? Запишіть формулу, за допомогою якої визначається крок кінематичного гвинта.
10. Чи можна складанням обертальних рухів тіла отримати його поступальний рух? Якщо так, то в якому випадку?
11. Тіло одночасно обертається навколо двох паралельних осей з кутовими швидкостями  с–1,
с–1, 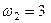 с–1. Обер-тання напрямлені в один бік. Який результуючий рух тіла? Яка швидкість результуючого руху?
с–1. Обер-тання напрямлені в один бік. Який результуючий рух тіла? Яка швидкість результуючого руху?
12. Тіло одночасно обертається навколо двох паралельних осей з кутовими швидкостями  с–1,
с–1, 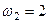 с–1. Обер-тання напрямлені в різні боки. Який результуючий рух тіла? Яка швидкість результуючого тіла?
с–1. Обер-тання напрямлені в різні боки. Який результуючий рух тіла? Яка швидкість результуючого тіла?
13. Що називається парою обертання? Який результуючий рух дає пара обертань? Яка швидкість результуючого руху?
14. Яким буде абсолютний рух тіла, котре одночасно обертається навколо двох осей, що перетинаються, з кутовою швидкостями  і
і  ? Яка швидкість результуючого руху?
? Яка швидкість результуючого руху?
15. Тіло одночасно обертається навколо чотирьох осей, які напрямлені вздовж сторін прямокутника  , як вказано на рис. А. Яким буде результуючий рух тіла і яка швидкість результуючого руху, якщо
, як вказано на рис. А. Яким буде результуючий рух тіла і яка швидкість результуючого руху, якщо  с–1,
с–1,  с–1?
с–1?
16. Тіло одночасно обертається навколо чотирьох осей, які напрямлені вздовж сторін прямокутника  , як вказано на рис. Б. Яким буде результуючий рух, якщо
, як вказано на рис. Б. Яким буде результуючий рух, якщо  с–1,
с–1,  с–1?
с–1?
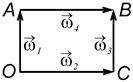 Рис. А
Рис. А
| 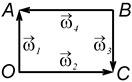 Рис. Б
Рис. Б
|
 17. Тіло обертається навколо осі
17. Тіло обертається навколо осі 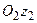 з кутовою швидкістю
з кутовою швидкістю 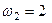 с–1 і одночасно навколо осі
с–1 і одночасно навколо осі  з кутовою швидкістю
з кутовою швидкістю  с–1, як вказано на рисунку. Осі
с–1, як вказано на рисунку. Осі  і
і 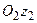 паралельні. Вказати положення миттєвої осі обертання тіла, якщо
паралельні. Вказати положення миттєвої осі обертання тіла, якщо  м.
м.
 18. Тіло одночасно обертається навколо двох паралельних осей
18. Тіло одночасно обертається навколо двох паралельних осей  і
і 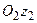 , як вказано на рисунку. Який буде резу-льтуючий рух тіла, якщо
, як вказано на рисунку. Який буде резу-льтуючий рух тіла, якщо 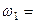
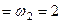 с–1,
с–1,  ? Визначити величину і вказати на рисунку вектор швидкості результуючого руху.
? Визначити величину і вказати на рисунку вектор швидкості результуючого руху.
 19. Диск обертається навколо вертикальної осі з кутовою швидкістю
19. Диск обертається навколо вертикальної осі з кутовою швидкістю  с–1 і навколо горизонтальної осі з кутовою швидкістю
с–1 і навколо горизонтальної осі з кутовою швидкістю  с–1, як вказано на рисунку. Яким є результуючий рух диска і яка швидкість результуючого руху?
с–1, як вказано на рисунку. Яким є результуючий рух диска і яка швидкість результуючого руху?
 20. Тіло одночасно бере участь у двох обертаннях з кутовими швидкостями
20. Тіло одночасно бере участь у двох обертаннях з кутовими швидкостями  с–1, вектори яких напрямлені вздовж ребер куба з стороною
с–1, вектори яких напрямлені вздовж ребер куба з стороною 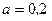 м, як вказано на рисунку. Яким буде абсолютний рух тіла? Знайти кінематичні характеристики цього
м, як вказано на рисунку. Яким буде абсолютний рух тіла? Знайти кінематичні характеристики цього
руху.
Аналогії між кінематикою і статикою
Отже, між векторами і , і є аналогія. Треба зауважити, що ця аналогія є зовнішньою (формальною), а не фізичною. Проте знання її необхідне для більш… Як видно з таблиці, більшість з наведених теорем доведена вище. Під номерами 4… Теорему про паралельний перенос вектора кутової швидкості сформулюємо за аналогією леми про паралельний перенос сили:Не змінюючи миттєвого розподілу швидкостей в тілі, вектор кутової швидкості можна паралельно перенести в будь-яку точку, якщо при цьому приєднати пару обертань, момент якої геометрично дорівнює моменту заданої кутової швидкості відносно точки переносу.
Доведення даної теореми є по суті повторенням доведення аналогічної теореми статики. Нехай деяке тверде тіло (рис. 157, а) обертається навколо осі  з кутовою швидкістю
з кутовою швидкістю  . В точці
. В точці  до тіла вздовж осі
до тіла вздовж осі  , яка паралельна осі
, яка паралельна осі  , приєднаємо еквівалентну нулеві сукупність обертань
, приєднаємо еквівалентну нулеві сукупність обертань  так, що
так, що  (рис. 157, б). Вектори
(рис. 157, б). Вектори  і
і  утворюють пару обертань, яку за формулою (2.109) замінено вільним вектором-моментом пари обертань
утворюють пару обертань, яку за формулою (2.109) замінено вільним вектором-моментом пари обертань
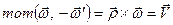 .
.

Рис. 157
В результаті в точці  (рис. 157, в) залишаться вектори
(рис. 157, в) залишаться вектори 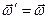 і
і  , які надаватимуть точкам тіла такі ж миттєві швидкості як і вектор
, які надаватимуть точкам тіла такі ж миттєві швидкості як і вектор  , що був прикладений в точці
, що був прикладений в точці  .
.
Отже, якщо при паралельному переносі вектора кутової швидкості  в довільну точку приєднується пара обертань, момент якої геометрично рівний моменту заданої кутової швидкості відносно точки переносу, то розподіл миттєвих швидкостей в тілі не зміниться.
в довільну точку приєднується пара обертань, момент якої геометрично рівний моменту заданої кутової швидкості відносно точки переносу, то розподіл миттєвих швидкостей в тілі не зміниться.
Отриману теорему використаємо для доведення теореми, яка за доведенням і змістом формально подібна (аналогічна) зведенню довільної системи сил до канонічного вигляду.
Теорема
Сукупність одночасних “n” поступальних рухів, швидкості яких , , ..., і “m” миттєвих обертальних рухів з кутовими швидкостями , , ..., твердого тіла, еквівалентна сукупності одного поступального і одного обертального рухів. Кутова швидкість результуючого обертання дорівнює геометричній сумі (головному вектору) кутових швидкостей складових обертань
 , (2.110)
, (2.110)
А швидкість результуючого поступального руху дорівнює геометричній сумі моментів кутових швидкостей відносно центра зведення і швидкостей поступальних рухів
 . (2.111)
. (2.111)
Оскільки кожний поступальний рух можна представити відповідною парою обертань, то геометрична сума (2.111) є не що інше, як головний момент кутових швидкостей відносно центра зведення.
Доведення сформульованої теореми з врахуванням наведених аналогій між статикою і кінематикою є дуже простим. Розглянемо тіло, яке одночасно здійснює 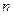 поступальних рухів з швидкостями
поступальних рухів з швидкостями  ,
,  , ...,
, ...,  і
і  миттєвих обертальних рухів з кутовими швидкостями
миттєвих обертальних рухів з кутовими швидкостями  ,
,  , ...,
, ...,  (рис. 158, а). Виберемо точку
(рис. 158, а). Виберемо точку  центром зведення. Враховуючи, що вектори кутових швидкостей
центром зведення. Враховуючи, що вектори кутових швидкостей  є ковзними векторами і, користуючись правилом їх паралельного переносу (див. попередню теорему), переносимо їх до центра
є ковзними векторами і, користуючись правилом їх паралельного переносу (див. попередню теорему), переносимо їх до центра  . В результаті такої
. В результаті такої
дії отримаємо сукупність векторів кутових швидкостей
( ,
,  , ...,
, ...,  ), прикладених до точки
), прикладених до точки  і пар обертань, моменти яких визначають відповідні поступальні рухи
і пар обертань, моменти яких визначають відповідні поступальні рухи
 ,
,  , ...,
, ..., 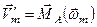 . (а)
. (а)
За правилом складання обертань навколо осей, що перетинаються, зведемо обертання з кутовими швидкостями
 ,
,  , ...,
, ...,  , які тепер прикладені до однієї точки
, які тепер прикладені до однієї точки  , до одного обертання з кутовою швидкістю, яка дорівнює геометричній сумі заданих кутових швидкостей
, до одного обертання з кутовою швидкістю, яка дорівнює геометричній сумі заданих кутових швидкостей
 . (б)
. (б)
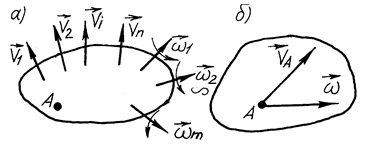
Рис. 158
Вектори швидкостей поступальних рухів  ,
,  , ...,
, ...,  є вільними векторами, то, паралельно перенісши їх до точки
є вільними векторами, то, паралельно перенісши їх до точки  і геометрично склавши, отримаємо
і геометрично склавши, отримаємо
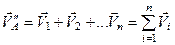 .
.
Склавши отриману швидкість  з швидкостями
з швидкостями  ,
, 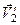 , ...,
, ..., 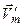 знайдемо швидкість результуючого поступального руху
знайдемо швидкість результуючого поступального руху
 .
.
Враховуючи (а), матимемо
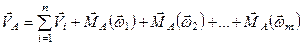
або
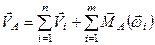 . (в)
. (в)
Отримані результати і рівності (б) і (в) підтверджують сформульовану теорему, отже вона доведена.
Розвиваючи далі аналогію між статикою і кінематикою, можна показати (читачу пропонується це проробити самостійно), що:
1. В кінематиці, як і в статиці, є два інваріанти, тобто дві величини, які не залежать від вибору центра зведення рухів. Першим інваріантом є головний вектор обертання, який визначається за формулою (2.110). Другим інваріантом є скаляр-ний добуток головного вектора обертання (формула 2.110) на головний момент (вектора швидкості результуючого поступального руху, формула (2.111)).
2. Якщо результуюча швидкість поступального руху (головний момент) дорівнює нулеві, то рух тіла, який складається з  обертальних рухів і
обертальних рухів і  поступальних рухів, зведеться до одного обертального руху, кутова швидкість якого визначається за формулою (2.110).
поступальних рухів, зведеться до одного обертального руху, кутова швидкість якого визначається за формулою (2.110).
3. Якщо кутова швидкість результуючого обертання (головний вектор обертання) дорівнює нулеві, то рух тіла, який складається з  обертальних рухів і
обертальних рухів і  поступальних рухів, зведеться до одного поступального руху, швидкість якого визначатиметься за формулою (2.111).
поступальних рухів, зведеться до одного поступального руху, швидкість якого визначатиметься за формулою (2.111).
4. За умови  ,
,  ,
,  результуючим рухом тіла буде обертальний рух навколо осі, що буде зміщена від центра зведення
результуючим рухом тіла буде обертальний рух навколо осі, що буде зміщена від центра зведення  на відстань
на відстань  .
.
5. Якщо вектор  ,
,  і вони не є взаємно перпендикулярними, тобто їх скалярний добуток
і вони не є взаємно перпендикулярними, тобто їх скалярний добуток  , відмінний від нуля, то вся система рухів твердого тіла зведеться до кінематичного гвинта.
, відмінний від нуля, то вся система рухів твердого тіла зведеться до кінематичного гвинта.
Все перераховане аналогічне частковим випадкам зведення довільної системи сил до заданого центра (§ 21).
Д О Д А Т К И
Проекція вектора на площину
Проекцією вектора 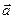 на площину є вектор
на площину є вектор  , який обмежений проекціями початку і кінця вектора
, який обмежений проекціями початку і кінця вектора 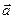 на задану площину (рис.1).
на задану площину (рис.1).

Рис. 1
Отже, щоб знайти проекцію деякого вектора 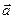 на якусь площину, наприклад, площину
на якусь площину, наприклад, площину 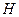 (див. рис. 1), необхідно з точки
(див. рис. 1), необхідно з точки  і
і  , які визначають початок і кінець вектора
, які визначають початок і кінець вектора 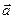 , опустити перпендикуляри
, опустити перпендикуляри  і
і  на задану площину. Основи цих перпендикулярів
на задану площину. Основи цих перпендикулярів 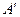 і
і  визначають проекції точок
визначають проекції точок  і
і  на площину
на площину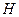 .
.
Проекція вектора на вісь
Проекцією вектора 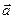 на вісь є скалярна алгебраїчна величина, яка дорівнює взятій з відповідним знаком довжині відрізка, обмеженого проекціями початку і кінця вектора
на вісь є скалярна алгебраїчна величина, яка дорівнює взятій з відповідним знаком довжині відрізка, обмеженого проекціями початку і кінця вектора 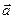 на задану вісь (рис.2).
на задану вісь (рис.2).

Рис. 2
Отже, щоб знайти проекцію деякого вектора 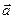 на якусь вісь, наприклад, вісь
на якусь вісь, наприклад, вісь  (див. рис. 2), необхідно з точок
(див. рис. 2), необхідно з точок  і
і  , які визначають початок і кінець вектора
, які визначають початок і кінець вектора 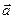 , опустити перпендикуляри
, опустити перпендикуляри 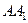 і
і 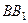 на задану вісь. Основи цих перпендикулярів (точки
на задану вісь. Основи цих перпендикулярів (точки 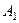 і
і  ) визначають проекції точок
) визначають проекції точок  і
і  на вісь
на вісь  , а відрізок
, а відрізок 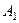
 – проекцію вектора
– проекцію вектора 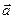 на вісь
на вісь  .
.
Проекція вектора на вісь найчастіше позначається тією ж літерою, що і вектор, з індексом осі на яку він проектується. В даному випадку 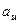 . Проекції вектора
. Проекції вектора 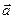 на декартові осі координат позначаються так:
на декартові осі координат позначаються так:  .
.
Проекція вектора на вісь вважається додатною, якщо напрям відрізка, що визначає цю проекцію, збігається з напрямом осі (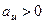 , див. рис. 2) і від’ємною – в протилежному випадку(
, див. рис. 2) і від’ємною – в протилежному випадку( , див. рис. 3,а).
, див. рис. 3,а).

Рис. 3
Якщо позначити 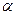 кут між вектором
кут між вектором  і додатним напрямом осі, то (див. рис. 3.б), отримаємо
і додатним напрямом осі, то (див. рис. 3.б), отримаємо
 , (Д.1)
, (Д.1)
тобто,
Проекція вектора на вісь дорівнює добутку модуля вектора на косинус кута між додатним напрямом осі і вектором, який проектується.
, якщо ; , якщо або ; , якщо (рис. 3).Рис. 4
Отриману проекцію  проектують на дану вісь
проектують на дану вісь  :
:  . Тут
. Тут 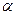 – кут між вектором
– кут між вектором  і додатним напрямом осі
і додатним напрямом осі  .
.
Приклади розв’язування задач на рівновагу тіла
Розв’язання. Розглянемо рівновагу вузла . На нього діє одна задана сила – це сила ваги ліхтаря (рис. 6). На вузол накладено дві в’язі: невагомі… Геометрична система рівноваги – це замкнутий силовий багатокутник. Для побудови його з точки , що береться поза…Рис. 9
Розв’язання. Розглянемо рівновагу блока  . На нього діють (рис. 10):
. На нього діють (рис. 10):
 – натяги частин
– натяги частин  і
і  троса, які, очевидно, є рівними між собою і чисельно дорівнюють вазі вантажу, тобто
троса, які, очевидно, є рівними між собою і чисельно дорівнюють вазі вантажу, тобто
 ;
;

Рис. 10
 – реакції невагомих стрижнів з шарнірами на кінцях. Ці реакції напрямлені вздовж прямих
– реакції невагомих стрижнів з шарнірами на кінцях. Ці реакції напрямлені вздовж прямих 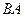 ,
, 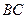 і
і 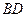 і дорівнюють шуканим зусиллям в стрижнях. До того ж, вважаючи, що всі стрижні працюють на розтяг, реакції їх напрямляємо від вузла
і дорівнюють шуканим зусиллям в стрижнях. До того ж, вважаючи, що всі стрижні працюють на розтяг, реакції їх напрямляємо від вузла  .
.
Отримана система сил є просторовою збіжною. Складаємо її рівняння рівноваги
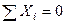
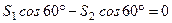 ;
;

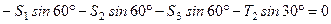 ;
;

 .
.
Звідси знаходимо

 .
.
Оскільки  , то остаточно отримаємо
, то остаточно отримаємо
 ,
,
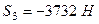 .
.
Знак мінус біля значення 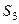 вказує на те, що відповідний стрижень, в даному випадку стрижень
вказує на те, що відповідний стрижень, в даному випадку стрижень 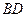 , працює на стиск.
, працює на стиск.
Задача 3.3. Знайти реакції жорсткого защемлення балки 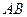 , яка завантажена на відрізку
, яка завантажена на відрізку 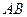 рівномірно розподіленим навантаженням інтенсивності
рівномірно розподіленим навантаженням інтенсивності 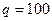 Н/м, в точці
Н/м, в точці 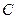 зосередженою силою
зосередженою силою  кН під кутом
кН під кутом  до балки і парою сил з моментом
до балки і парою сил з моментом  кН×м. Розміри вказані на рис. 11.
кН×м. Розміри вказані на рис. 11.
Розв’язання. За об’єкт рівноваги вибираємо балку 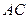 . Активними силами, прикладеними до балки, будуть: сила
. Активними силами, прикладеними до балки, будуть: сила  ; пара сил з моментом
; пара сил з моментом  ; рівномірно розподілене навантаження
; рівномірно розподілене навантаження  , рівнодійна якого дорівнює
, рівнодійна якого дорівнює

Рис. 11
 .
.
В’яззю, накладеною на балку, є жорстке защемлення  . Заміняємо дію цієї в’язі реакціями
. Заміняємо дію цієї в’язі реакціями  і реактивним моментом
і реактивним моментом  .
.
На балку 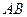 діє плоска довільна система сил. Рівняння рівноваги
діє плоска довільна система сил. Рівняння рівноваги
 ;
;
 ;
;
 .
.
Розв’язуючи цю систему рівнянь, отримаємо
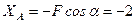 кН ,
кН ,
 кН ,
кН ,
 кН×м .
кН×м .
Задача 3.4. Плита 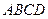 вагою
вагою 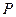 утримується в горизонтальному положенні за допомогою сферичного шарніра
утримується в горизонтальному положенні за допомогою сферичного шарніра  , завіси
, завіси  і невагомого стрижня
і невагомого стрижня  , розміщеного в площині, паралельній координатній площині
, розміщеного в площині, паралельній координатній площині 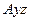 (рис. 12). У площині плити діє пара сил з моментом
(рис. 12). У площині плити діє пара сил з моментом  . Визначити реакції опор і зусилля в стрижні
. Визначити реакції опор і зусилля в стрижні  , якщо
, якщо  кН,
кН, 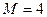 кН,
кН,  м,
м,  м,
м,  .
.

Рис. 12
Розв’язання. Об’єкт рівноваги – плита. Активна сила  , пара сил з моментом
, пара сил з моментом  , реакції в’язей
, реакції в’язей  показані на рис. 12. На плиту діє довільна просторова система сил, для якої запишемо рівняння рівноваги
показані на рис. 12. На плиту діє довільна просторова система сил, для якої запишемо рівняння рівноваги
 ;
;
 ;
;
 ;
;
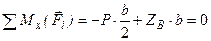 ;
;
 ;
;
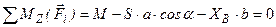 .
.
Розв’язуючи отриману систему рівнянь знаходимо невідомі реакції

 ;
;
 ;
;  ;
;
 ;
;  .
.
Додавання двох паралельних сил
Теорема
Дві паралельні сили і , які направлені в один бік, мають рівнодійну, яка напрямлена в той же бік і за модулем дорівнює сумі цих сил. Лінія дії рівнодійної поділяє відстань між лініями дій заданих сил на частини, які обернено пропорційні величинам сил і .
Для доведення даної теореми розглянемо тверде тіло(на рис. 13 не показано), до якого прикладено дві паралельні сили  і
і  , які направлені в один бік (рис. 13, а).
, які направлені в один бік (рис. 13, а).
З’єднаємо дві точки  і
і  прямою лінією і прикладемо в даних точках дві рівні за величиною і протилежні за напрямом сили
прямою лінією і прикладемо в даних точках дві рівні за величиною і протилежні за напрямом сили  і
і  , які напрямлені вздовж прямої
, які напрямлені вздовж прямої 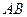 . Такі дві сили, оскільки, вони взаємно зрівноважуються згідно з аксіомою 2, не змінюють стану тіла. За правилом паралелограма попарно додамо сили (рис. 13, б)
. Такі дві сили, оскільки, вони взаємно зрівноважуються згідно з аксіомою 2, не змінюють стану тіла. За правилом паралелограма попарно додамо сили (рис. 13, б)
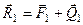 ,
, 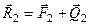 .
.
Отримані рівнодійні 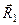 і
і  перенесемо вздовж лінії їх дії в точку
перенесемо вздовж лінії їх дії в точку  (це також не змінить стану тіла, оскільки сила є ковзним вектором), де розкладемо їх на початкові складові (рис. 13, в)
(це також не змінить стану тіла, оскільки сила є ковзним вектором), де розкладемо їх на початкові складові (рис. 13, в)
 ,
,  .
.
Сили  і
і  , прикладені в точці
, прикладені в точці  , взаємно зрівноважуються і їх можна відкинути, не змінюючи стану тіла. Залишаються дві сили
, взаємно зрівноважуються і їх можна відкинути, не змінюючи стану тіла. Залишаються дві сили  і
і  , які прикладені в точці
, які прикладені в точці  , напрямлені вздовж однієї прямої в один і той же бік. Додаючи ці дві сили, одержимо їх рівнодійну
, напрямлені вздовж однієї прямої в один і той же бік. Додаючи ці дві сили, одержимо їх рівнодійну 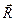 , яка має величину, що дорівнює сумі їх величини
, яка має величину, що дорівнює сумі їх величини

і напрямлена вздовж тієї ж прямої і в той же бік.

Рис. 13
Отже, сили  і
і  (рис. 13, а) мають рівнодійну, величина якої дорівнює сумі сил
(рис. 13, а) мають рівнодійну, величина якої дорівнює сумі сил  і
і  , паралельна до них і напрямлена в той же бік (рис. 13, г).
, паралельна до них і напрямлена в той же бік (рис. 13, г).
Тепер визначимо, де проходить лінія дії рівнодійної, тобто визначимо положення точки 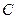 перетину цієї лінії з відрізком
перетину цієї лінії з відрізком 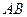 . Для цього співставимо трикутники
. Для цього співставимо трикутники 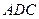 і
і 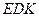 ,
, 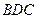 і
і  . Вони є попарно подібними, тобто:
. Вони є попарно подібними, тобто:


 ,
, 

 .
.
З подібності трикутників маємо
 ,
,
 .
.
Звідси
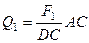 ,
, 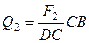 .
.
Оскільки 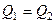 , то остаточно отримаємо
, то остаточно отримаємо
 ,
,
тобто
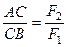 .
.
Отже, точка 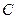 поділяє відрізок
поділяє відрізок 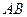 на частини, які обернено пропорційні величинам сил.
на частини, які обернено пропорційні величинам сил.
Таким чином, теорема доведена.
Аналогічно, що пропонується читачу проробити самостійно, можна довести і таку теорему:
Дві не рівні за модулем паралельні сили і , які напрямлені в протилежні боки, мають рівнодійну, напрям якої співпадає з напрямом більшої сили, а модуль її дорівнює різниці модулів складових сил і . Лінія дії рівнодійної поділяє відстань між лініями дії складових сил зовнішнім чином на відрізки, які обернено пропорційні величинам цих сил, тобто, якщо , то , і точка знаходиться за межами відрізка з боку більшої сили, як вказано на рис. 14.

Рис. 14
Доведення теореми про еквівалентність пар сил
Покажемо, що задану пару сил , не змінюючи стану тіла, на яке вона діє, можна перенести так, щоб її плече збігалося з відрізком . Для цього в точках…Рис. 15
Сили  ,
,  ,
, 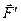 і
і 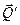 перенесемо вздовж ліній їх дій відповідно в точки
перенесемо вздовж ліній їх дій відповідно в точки  і
і  і попарно їх додамо (рис. 15, в)
і попарно їх додамо (рис. 15, в)
 ,
, 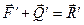 .
.
Враховуючи те, що  ,
,  , отримаємо, що
, отримаємо, що 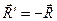 . До того ж рівнодійні
. До того ж рівнодійні 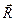 і
і 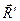 будуть напрямлені вздовж діагоналі
будуть напрямлені вздовж діагоналі  ромба
ромба  , бо сили
, бо сили  ,
,  ,
, 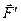 ,
, 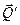 рівні за модулем і при їх додаванні отримується ромб. Таким чином, сили
рівні за модулем і при їх додаванні отримується ромб. Таким чином, сили 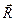 і
і 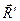 дорівнюють одна одній за величиною і діють вздовж однієї прямої в протилежні боки (рис. 15, в). Отже, вони взаємно зрівноважуються і їх, не змінюючи стану тіла, можна виключити.
дорівнюють одна одній за величиною і діють вздовж однієї прямої в протилежні боки (рис. 15, в). Отже, вони взаємно зрівноважуються і їх, не змінюючи стану тіла, можна виключити.
Після всіх цих дій залишаються сили 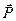 і
і 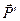 , які прикладені в точках
, які прикладені в точках 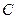 і
і  (рис. 15, г). Сили
(рис. 15, г). Сили 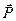 і
і 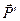 рівні за модулем, паралельні і протилежні за напрямом, отже вони утворюють пару сил. Оскільки
рівні за модулем, паралельні і протилежні за напрямом, отже вони утворюють пару сил. Оскільки  ,
, 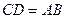 , то можна вважати, що отримана пара сил
, то можна вважати, що отримана пара сил  є не що інше, як пара сил
є не що інше, як пара сил 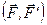 , яка перенесена з початкового положення
, яка перенесена з початкового положення 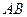 в потрібне положення
в потрібне положення 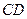 і це перенесення не змінило стану тіла.
і це перенесення не змінило стану тіла.
Доведення теореми 2. Для доведення другої теореми припустимо, що дано пару сил 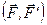 з плечем
з плечем 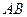 , яка знаходиться в площині
, яка знаходиться в площині  , і задано деяку площину
, і задано деяку площину  , яка паралельна площині
, яка паралельна площині  (рис. 16, а). Доведемо що задану пару сил
(рис. 16, а). Доведемо що задану пару сил 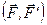 , не змінюючи стану тіла, на яке вона діє (тіло на рис. 16 не зображено), можна перенести в площину
, не змінюючи стану тіла, на яке вона діє (тіло на рис. 16 не зображено), можна перенести в площину  . Для цього з точок
. Для цього з точок  і
і  проведемо паралельні прямі, точки перетину яких з площиною
проведемо паралельні прямі, точки перетину яких з площиною 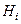 позначимо
позначимо 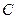 і
і  . В отриманих точках перпендикулярно до відрізка
. В отриманих точках перпендикулярно до відрізка 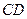 в протилежних напрямах прикладемо по дві сили
в протилежних напрямах прикладемо по дві сили 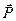 і
і  ,
, 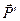 і
і 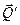 , які задовольняють умові
, які задовольняють умові  (рис. 16, б). Оскільки прикладені сили попарно зрівноважуються, то їх прикладання не змінить стану тіла.
(рис. 16, б). Оскільки прикладені сили попарно зрівноважуються, то їх прикладання не змінить стану тіла.
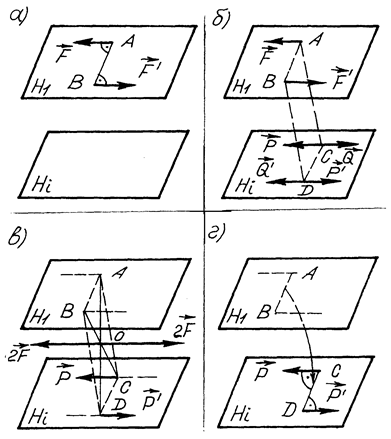
Рис. 16
Додаємо силу  і
і 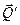 . Оскільки ці сили рівні, паралельні і напрямлені в один бік, то їх рівнодійна дорівнює за величиною
. Оскільки ці сили рівні, паралельні і напрямлені в один бік, то їх рівнодійна дорівнює за величиною 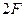 , їм паралельна і напрямлена в той же бік. Точка її прикладання поділяє відрізок
, їм паралельна і напрямлена в той же бік. Точка її прикладання поділяє відрізок  навпіл. Точно так само, додаючи сили
навпіл. Точно так само, додаючи сили 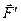 і
і  , які прикладені відповідно в точках
, які прикладені відповідно в точках  і
і 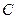 , одержимо їх рівнодійну, яка за величиною дорівнює
, одержимо їх рівнодійну, яка за величиною дорівнює 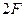 їм паралельна і напрямлена в той же бік, що й ці сили. Точка прикладання цієї рівнодійної поділяє навпіл відрізок
їм паралельна і напрямлена в той же бік, що й ці сили. Точка прикладання цієї рівнодійної поділяє навпіл відрізок 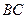 (рис. 16, в). Відрізки
(рис. 16, в). Відрізки  і
і 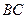 поділяються навпіл в точці перетину
поділяються навпіл в точці перетину  , бо вони є діагоналлю паралелограма
, бо вони є діагоналлю паралелограма  . Таким чином, обидві рівнодійні, які рівні за величиною і протилежні за напрямом, прикладені в одній точці
. Таким чином, обидві рівнодійні, які рівні за величиною і протилежні за напрямом, прикладені в одній точці  (рис. 16, в). Отже, вони взаємно зрівноважуються і їх можна виключити.
(рис. 16, в). Отже, вони взаємно зрівноважуються і їх можна виключити.
Залишаються сили 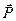 і
і 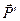 , які рівні за величиною, протилежно напрямлені і паралельні (рис. 16, г), тобто становлять пару сил з плечем
, які рівні за величиною, протилежно напрямлені і паралельні (рис. 16, г), тобто становлять пару сил з плечем 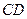 . Оскільки
. Оскільки  ,
,  ,
, 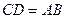 , то можна вважати, що отримана пара сил
, то можна вважати, що отримана пара сил  є не що інше, як пара сил
є не що інше, як пара сил 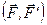 , яка перенесена з площини
, яка перенесена з площини  в паралельну площину
в паралельну площину  і це перенесення не змінило стану тіла.
і це перенесення не змінило стану тіла.
Доведення теореми 3. Для доведення третьої теореми розглянемо пару сил  з плечем
з плечем  , яка діє на тверде тіло (тіло не зображено на рисунку) в площині рисунка (рис, 17, а). На лінії дії сили
, яка діє на тверде тіло (тіло не зображено на рисунку) в площині рисунка (рис, 17, а). На лінії дії сили 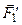 вибираємо довільну точку
вибираємо довільну точку  і, використовуючи те, що сила є ковзним вектором, перенесемо силу
і, використовуючи те, що сила є ковзним вектором, перенесемо силу 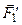 в цю точку (рис.17, б). Сили
в цю точку (рис.17, б). Сили  і
і  розкладемо на дві складові
розкладемо на дві складові
 ,
, 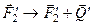
так, що сили  і
і  розміщені перпендикулярно до відрізка
розміщені перпендикулярно до відрізка  , а сили
, а сили  і
і 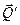 – вздовж цього відрізка (рис. 17, в).
– вздовж цього відрізка (рис. 17, в).
Позначимо  , тоді
, тоді  ,
,  , як кути з відповідно перпендикулярними сторонами. З прямокутних
, як кути з відповідно перпендикулярними сторонами. З прямокутних і
і  маємо
маємо
 ,
,
 ,
,
 ,
,
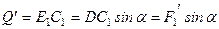 .
.

Рис. 17
Оскільки  , то
, то  ,
,  .
.
Сили  і
і 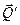 , які діють вздовж однієї прямої в протилежні боки, зрівноважуються і їх, не змінюючи стану тіла, можна виключити.
, які діють вздовж однієї прямої в протилежні боки, зрівноважуються і їх, не змінюючи стану тіла, можна виключити.
Після виключення сил  і
і 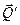 залишаються сили
залишаються сили  і
і  , які рівні за величиною, протилежно напрямлені і паралельні (рис. 17, г), тобто утворюють пару сил з плечем
, які рівні за величиною, протилежно напрямлені і паралельні (рис. 17, г), тобто утворюють пару сил з плечем  . Отримана пара сил
. Отримана пара сил  діє на тверде тіло так само, як задана пара сил
діє на тверде тіло так само, як задана пара сил  , бо всі перетворення, які були проведені з силами, не змінювали стану тіла. Визначимо момент отриманої пари сил
, бо всі перетворення, які були проведені з силами, не змінювали стану тіла. Визначимо момент отриманої пари сил
 .
.
З  маємо
маємо
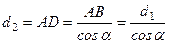 .
.
Враховуючи, що  , а
, а 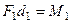 , отримаємо
, отримаємо
 .
.
Отже пари сил, які однаково діють на тверде тіло, мають рівні за величиною і однакові за знаком моменти. Тобто, не змінюючи дії пари сил на тіло, можна змінювати модулі сил і плече цієї пари, але так, щоб її момент і напрям обертання залишались незмінними.
Найменше значення головного моменту системи сил
Для визначення найменшого значення головного моменту системи сил довільну систему сил, яка не зображена на рис. 18, послідовно зведемо до двох центрів (точок):  – довільна точка;
– довільна точка;  – точка, яка знаходиться на центральній осі системи (рис. 18).
– точка, яка знаходиться на центральній осі системи (рис. 18).
Позначимо відстань центра зведення  до центральної осі системи через
до центральної осі системи через 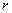 , тоді (див. § 21)
, тоді (див. § 21)
 .
.

Рис. 18
Отже,
 ,
,
 .
.
Величина головного моменту відносно будь-якої точки зведення  і кутнахилу його до головного вектора залежить від відстані даної точки до центральної осі системи. З отриманих формул можна зробити такі висновки:
і кутнахилу його до головного вектора залежить від відстані даної точки до центральної осі системи. З отриманих формул можна зробити такі висновки:
1. Для всіх центрів зведення, які знаходяться на одній і тій же відстані 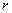 від центральної осі (тобто лежать на поверхні колового циліндра, вісь якого є центральною віссю даної системи і радіус основи якого дорівнює
від центральної осі (тобто лежать на поверхні колового циліндра, вісь якого є центральною віссю даної системи і радіус основи якого дорівнює 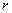 ), головний момент системи сил
), головний момент системи сил  має одну і ту ж величину і утворює один і той же кут з головним вектором
має одну і ту ж величину і утворює один і той же кут з головним вектором 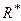 . Цим і пояснюється термін “центральна вісь системи”.
. Цим і пояснюється термін “центральна вісь системи”.
2. Величина головного моменту і його кут нахилу до головного вектора зростають разом із зростанням  .
.
3. Головний момент має найменше значення для  , тобто відносно точок центральної осі системи.
, тобто відносно точок центральної осі системи.
Отже, відносно точок центральної осі системи величина головного моменту має найменше значення, яке дорівнює (див. § 21) проекції головного моменту  відносно довільної точки на напрям головного вектора
відносно довільної точки на напрям головного вектора
 .
.
Якщо цю рівність домножити і поділити на величину головного вектора, то отримуємо формулу для обчислення найменшого значення головного моменту
 ,
,
або
 .
.
Список використаної літератури, деяких підручників і навчальних посібників з теоретичної механіки
2. Айзерман М.А. Классическая механика. – М.: Наука, 1974. – 357 с. 3. Бать М.И., Джанилидзе Г.Ю., Кельзон А.С. Теоретичес-кая механика в примерах… 4. Бражниченко Н.А., Кан В.Л., Минцберг Б.Л. Сборник задач по теоретической механике. – М.: Высш. шк., 1974. – 520…Предметний покажчик
Аксіома дії і протидії 18 – зрівноваження двох сил 16 – накладання додаткових в’язей 18– Конец работы –
Используемые теги: Предмет, теоретичної, механіки, теоретична, механіка, одна, дисциплін, науки, механіка0.135
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Предмет теоретичної механіки Теоретична механіка – це одна з дисциплін науки Механіка
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов