Абсолютна швидкість точки, яка здійснює складний рух, дорівнює геометричній сумі її переносної і відносної швидкостей.

§ 44.3 Теорема про складання пришвидшень
(Теорема Коріоліса)

З попереднього (див. векторну рівність (е)) маємо

Якщо цю рівність ще раз продиференціювати за часом, то отримаємо

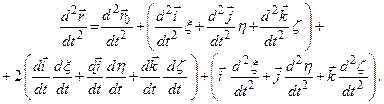(ж)

З’ясуємо зміст кожного доданка отриманої рівності.

1. Оскільки друга похідна за часом від радіуса-вектора є пришвидшення відповідної точки, то – абсолютне пришвидшення точки , яка здійснює складний рух (див.
формулу (а)).

– пришвидшення точки .

2. Вираз 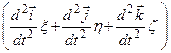є не що інше, як друга похідна від 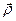за часом за умови, що тобто:

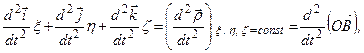
адже 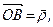до того ж 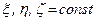справедливе тільки для точки .

3. Аналогічно вираз 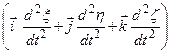є другою похідною від 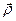за часом за умови, що 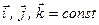, тобто:

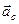4. Вираз позначається і називається додатковим (коріолісовим або поворотним при-швидшенням). Коріолісовим пришвидшення назване в честь французького механіка Гюстава Гаспара Коріоліса (1792-1843), котрим в 1833 р. була виведена теорема, що буде сформульована нижче. Однак треба відзначити, що вперше ця теорема була сформульована Л. Ейлером у 1765 р., потім К.Гаусом у 1803 р. Зміст інших назв вектора 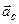виясниться пізніше.

Враховуючи сказане, векторна рівність (ж) набуває вигляду

.

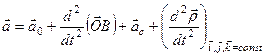За формулою (2.32) маємо, що

.

Оскільки пришвидшення точки В для точки К є переносним (, див. формулу (в)), то

.

Згідно з формулою (б)

.

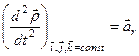Враховуючи це, остаточно матимемо

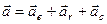. (2.59)

Отримана формула виражає теорему Коріоліса, яка читається так: