Выпуклость графика функции. Точки перегиба
Определение 1. График дифференцируемой функции f(x) называется выпуклым вниз на интервале (а, b), если он расположен выше любой своей касательной на этом интервале (рис. 11).
График функции f(x) называется выпуклымвверх на интервале (a, b), если он расположен ниже любой своей касательной в этом интервале (рис. 12).
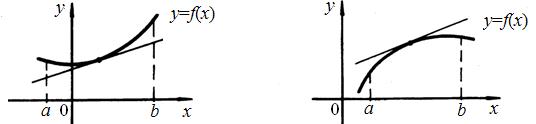
Рис. 11 Рис. 12
Так, парабола у = х2 является выпуклой вниз на всей числовой оси (рис.13), а полуокружность 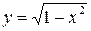 (рис. 14) имеет график, выпуклый вверх на отрезке (-1, 1).
(рис. 14) имеет график, выпуклый вверх на отрезке (-1, 1).
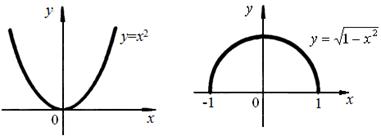
Рис. 13 Рис. 14
Определение 2. Точкой перегиба графика функции f(x) называется точка графика непрерывной функции М0(х0, f(x0)), отделяющая его части разной выпуклости (рис. 15).
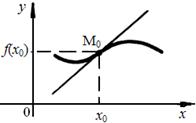
Рис. 15
Для определения интервалов выпуклости вверх и вниз используют знак второй производной функции f(x).
Теорема 1 (достаточное условие точки выпуклости). Если функция f(x) во всех точках интервала (a, b) имеет отрицательную вторую производную, т.е. f″(х) < 0, то график функции в этом интервале выпуклый вверх. Если же f″(x) > 0 для всех х є (a, b), то график функции выпуклый вниз в этом интервале.
Доказательство. Пусть f″(х) < 0 для любого х є (a, b). Возьмем на графике произвольную точку М с абсциссой х0 є (a, b) и проведем через М касательную (рис. 16).
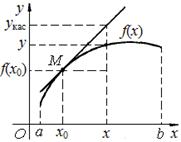
Рис. 16
Покажем, что график функции расположен ниже этой касательной. Для этого сравним в точке х є (a, b) ординату y кривой y = f(х) с ординатой yкас ее касательной.
Уравнение касательной yкас – f(х0) = f'(x0) (х – x0), т.е. yкас = f(х0) + f'(x0) (х – x0).
Тогда y – yкас = f(х) – f(х0) – f'(x0) (х – x0).
По теореме Лагранжа, f(х) – f(х0) = f'(с) (х – x0), где с лежит между x0 и х. Поэтому
y – yкас = f'(с) (х – x0) – f'(x0) (х – x0),
т.е.
y – yкас = (f'(с) – f'(x0)) (х – x0).
Разность f'(с) – f'(x0) снова преобразуем по формуле Лагранжа:
f'(с) – f'(x0) = f''(с1) (с – x0), где с1 лежит между х0 и с.
Поэтому
y – yкас = f''(с1) (с – x0) (х – x0).
Исследуем это равенство:
1) если х > x0, то х – x0 > 0, с – x0 > 0 и f''(с1) < 0. Следовательно, y – yкас < 0, т.е. y < yкас.
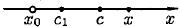
2) если х < x0, то х – x0 < 0, с – x0 < 0 и f''(с1) < 0. Следовательно, y – yкас < 0, т.е. y < yкас.
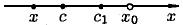
Итак, доказано, что во всех точках интервала (a, b) ордината касательной больше ординаты графика, т.е. график функции выпуклый вверх.
Аналогично доказывается, что при f″(x) > 0 график выпуклый вниз.
Следствие теоремы 1 (необходимое условие точки перегиба графика функции). Если точка М0(х0, f(x0)) является точкой перегиба графика f(x), то вторая производная f″(x0) равняется нулю или не существует.
Действительно, стоит только предположить противное, т.е. существует f″(x0) ≠ 0, как тотчас же, согласно теоремы 1, точка М0 не оказывается точкой перегиба, а является точкой выпуклости, что противоречит условию следствия.
Таким образом, точки перегиба следует искать среди тех точек, в которых вторая производная f″(x) = 0 или не существует.
Для нахождения точек перегиба графика функции используется следующая теорема.
Теорема 2.(достаточное условие существования точек перегиба). Если вторая производная f″(x) при переходе через точку x0, в которой она равна нулю или не существует, меняет знак, то точка графика М0(х0, f(x0)) является точкой перегиба.
Доказательство. Пусть f″(x) < 0 при х < x0 и f″(x) > 0 при х > x0. Это значит, что слева от x0 график выпуклый вверх, а справа – выпуклый вниз. Следовательно, точка графика (х0, f(x0)) является точкой перегиба.
Аналогично доказывается, что если f″(x) > 0 при х < x0 и f″(x) < 0 при х > x0, то точка (х0, f(x0)) – точка перегиба графика функции f(x).
Пример. Исследовать на выпуклость и точки перегиба график функции
y = x5 – x + 5.
Решение. y' = 5x4 – 1, y'' = 20x3. Вторая производная существует на всей числовой оси; y'' = 0 при х = 0.
Отмечаем, что y'' < 0 при х < 0; y'' > 0 при х > 0. Следовательно, график функции в интервале (-∞; 0) – выпуклый вверх, в интервале (0; ∞) – выпуклый вниз. Точка (0; 5) – точка перегиба.