Асимптоты графика функции
Определение 1. Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой.
Асимптоты могут быть вертикальными, наклонными и горизонтальными.
Определение 2. Прямая x = a является вертикальной асимптотой графика f(x), если 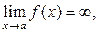 или
или  (рис. 17), или
(рис. 17), или 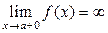 .
.

Рис. 17
Для отыскания вертикальных асимптот следует найти те значения х, вблизи которых функция f(x) неограниченно возрастает по модулю. Обычно это точки разрыва 2-го рода.
Например, кривая 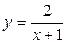 имеет вертикальную асимптоту х = -1, так как
имеет вертикальную асимптоту х = -1, так как 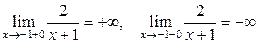 (рис. 18).
(рис. 18).
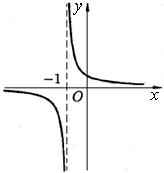
Рис. 18
Теорема. Прямая у = kх + b является наклонной асимптотой графика f(x) тогда и только тогда, когда существуют пределы
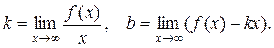
Доказательство.
1) Дано: 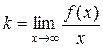 и
и 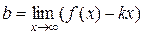 . Доказать, что у = kх + b – асимптота графика f(x).
. Доказать, что у = kх + b – асимптота графика f(x).
Используя связь между пределом функции и бесконечно малой величиной, запишем: f(x) – kx = b + β(x), где 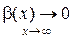 – б.м.ф.
– б.м.ф.
Тогда f(x) – (kx + b) = β(x) → 0 при х → ∞. Левая часть последнего равенства является разностью ординат точки кривой M и точки прямой М1 (рис. 19): |MМ1|→0. Из прямоугольного треугольника MPМ1 следует, что когда гипотенуза |MМ1| → 0, то и катет |MP| = d → 0. Тогда, согласно определению асимптоты, прямая у = kх + b будет асимптотой графика f(x).

Рис. 19
2) Дано: у = kх + b – асимптота графика f(x). Доказать, что существуют пределы 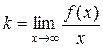 и
и 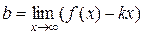 .
.
Из определения асимптоты следует, что расстояние между точкой кривой М и точкой прямой P стремится к нулю, значит, является бесконечно малой величиной (|MP| = d = α(x) → 0 при х → ∞, где α(x) – б.м.ф.) (рис. 19).
Запишем разность ординат точки кривой M и точки прямой P, используя связь между пределом функции и бесконечно малой величиной (здесь kх + b является пределом функции f(x) при х → ∞): f(x) = kx + b + α(x). Тогда
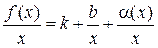 ;
; 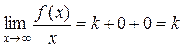 .
.
b = f(x) – kx – α(x) = 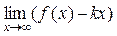 . Теорема доказана.
. Теорема доказана.
Для горизонтальной асимптотыу = b выполняется k = 0 и b =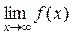 .
.
Замечание 1. Если хотя бы один из пределов k (угловой коэффициент прямой) или b (сдвиг прямой по оси Оy) не существует или равен бесконечности, то кривая наклонной асимптоты не имеет.
Замечание 2. Асимптоты графика функции f(x) при х → +∞ и х → -∞ могут быть разными. Поэтому при нахождении пределов k и b случаи, когда х → +∞ и когда х → -∞, следует рассматривать раздельно.
Пример.На графике (рис. 20) точки х2, х4 – точки экстремумов функции, точка х1 – точка перегиба.
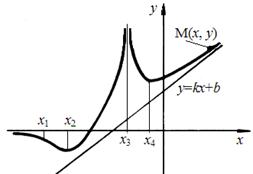
Рис. 20
Точка х3 – точка разрыва функции 2-го рода; прямая х = х3 является вертикальной асимптотой графика функции.
Прямая х = 0 – горизонтальная асимптота, а у = kх + b – наклонная асимптота графика.