Параметрических характеристик

1.1. Управление рисками на основе их вероятностных

параметрических характеристик.

Одними из важнейших вероятностных параметрических характеристик рисков (т.н., статистик) являются отклонение (D) и среднеквадратичное или стандартное отклонение (s), например, нормы прибыли r от ее ожидаемого среднего значения M(r)

D = r – M(r), (1.1.1)

s(r) = {M[r – M(r)]²}^1/2.

Математическое ожидание случайной величины F определяется по разному для ее дискретных и непрерывных значений

M(F) = å_k f_k Pr(f_k) – для дискретных значений, (1.1.2)

M(F) = òf p(f) df – для непрерывных значений,

где: Pr(f_k) – вероятность события, при котором случайная величина F принимает значение f_k (см. модуль 1, глава 2, стр. 24); p(f) – плотность вероятности значений случайной величины F (см. модуль 1, глава 2, стр. 46). Суммирование и интегрирование в (1.1.2) распространяются на весь диапазон значений случайной величины – область ее определения. Произведение p(f) df определяет вероятность попадания случайной величины F в бесконечно малый интервал между значениями f и f + df.

Если r^* = M(r) – процентная ставка кредита, а r – доходность по какой либо операции наращивания этого кредита, то D = r – r^* может быть либо выигрышем, либо убытком. Таким образом общая величина убытка характеризуется абсолютным значениемú Dú =ú r – r^*ú.

Другими важными характеристиками риска являются вероятности отклонений (убытков)

Pr(D_k) = Pr(f_k – f^*) для дискретных значений и (1.1.3)

Pr(D) = Pr(D > D^*) = 1 –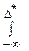p(f – f^*) df для непрерывных.

Из неравенства Чебышева известна связь между линейным D = r – M(r) и среднеквадратичным отклонением

Pr(ú r – M(r)ú > d) £ s ²(r) /d ² . (1.1.4)

Отсюда видно, что незначительному риску по среднеквадратичному отклонению соответствует малый риск и по линейному отклонению. Следовательно D и s являются эквивалентными характеристиками рисков.

Многокритериальная трактовка риска. Иногда риски описывают векторными двухпараметрическими характеристиками, связанными с рисками-отклонениями и рисками-вероятностями L = [D, Pr(D)], рисками-отклонениями и рисками больших ожидаемых значений прибыли L = [s, M], рисками потери активов при ограниченных собственных капиталах L = [активы с весами Pr(D), собственный капитал].

Пример 1.1.1. На рынке ценных бумаг могут возникнуть два исхода и на каждый из них акции A и B откликаются неслучайным образом. Вероятности этих исходов и соответствующие им доходности акций показаны в таблице 1.1.1a.

Таблица 1.1.1a

	Исход 1	Исход 2
	Доходность, r	Вероятность, Pr	Доходность, r	Вероятность, Pr
A	5 %	0,2	1,25 %	0,8
B	-1 %	0,2	2,75 %	0,8

Отсюда следует: M(r_A) = 5 % * 0,2+1,25 %* 0,8 = 2 %;

M(r_B) = -1 % * 0,2+2,75 %* 0,8 = 2 %;

s_A = (5-2)² * 0,2 + (1,25-2)² * 0,8 = 2,25;

s_B = (-1-2)² * 0,2 + (2,75-2)² * 0,8 = 2,25.

Статистический коэффициент связи (корреляции) откликов акций получается отрицательным

cor_AB = = (1.1.5)

= –1.

Предположим, что инвестор взял деньги в долг под процент r^* = 1,5 %. Тогда он получит следующие доходы по акциям, приобретенным на заемные деньги

 

Таблица 1.1.1б

	Исход 1	Исход 2
	Доход, D	Вероятность, Pr	Доход, D	Вероятность, Pr
A	5 % -1,5 % = = 3,5 %	0,2	1,25 %-1,5 % = = -0,25%	0,8
B	-1 % -1,5 % = = -2,5 %	0,2	2,75 %-1,5 % = = 1,25%	0,8

Ожидаемые риски-потери (П) и риски-вероятности (Pr) при покупке разных акций

П_A = 0,8*0,25% = 0,2% < П_B = 0,2*2,5% = 0,5%;

Pr_A = 0,8 > Pr_B = 0,2.

Таким образом в случае A риски-потери меньше, но риски-вероятности больше. Как действовать в подобной ситуации инвестору зависит от его индивидуальных предпочтений, выражаемых, в том числе, функцией полезности дохода.

Скаляризация двухпараметрических характеристик рисков. Для упрощения оптимизации двухпараметрические характеристики риска сводят к скалярным

L = D * Pr(D), П *Pr(П) Þ min (1.1.6)

– минимизация средних потерь,

L = s / M Þ min (1.1.7)

– минимизация коэффициента вариации,

L = П *Pr(П) /K Þ min (1.1.8)

– минимизация коэффициента риска при заданном собственном капитале K,

L = K / [П * Pr(П)] ³ Þ max (1.1.9)

– максимизация коэффициента Кука (используется, в частности, для оценки финансовой стабильности коммерческих банков),

L = a * r – b * r ² Þ max (1.1.10)

– максимизация функции полезности Неймана-Монгенштерна.

Диверсификацию (разделение) используют как метод управления для снижения риска разорения (разделение вклада по вложениям и разделение капитала на собственный и заемный).

Диверсификация вложений. Пусть a_A и a_B (a_A+a = 1) – доли вложений в акции A и B. Тогда доходность смеси

r = a_A r_A + a_B r_B = a_A r_A + (1 – a_A) r_B. (1.1.11)

Для каждой ситуации таблицы 1.1.1 легко получить гарантированные условия неразорения

r₁ = 5 % a_A + (1 – a_A) (-1 %) = 6 % a_A – 1% > 1,5% ,

r₂ = 1,25 % a_A + (1 – a_A) 2,75 % =

= 2,75 % – 1,5 % a_A > 1,5 % .

Решая эту систему неравенств, получим

0,42 % < a_A < 0,83 % .

Полная обратная корреляция активов (cor_AB = –1) при одинаковых парциальных рисках (s_A = s_B) позволяет распределить вложения таким образом, чтобы получить безрисковую по среднеквадратичной характеристике смесь. С учетом (1.1.5) дисперсия s_å² смеси å = a_A A +a_B B равна

s_å² = a_A² s_A² + a_B² s_B² + 2 a_Aa_B cor_AB s_As_B = (1.1.12)

= a_A² s_A² + a_B² s_B² – 2a_Aa_B s_A s_B = s_A² (a_A – a_B)².

Таким образом, выбирая a_A = a_B = 1/2, инвестор добивается детерминированной доходности 2 % при s ²_å = 0, что избавляет его от риска разорения.

Диверсификация капитала. Предположим, что инвестиции A=К+З в какой либо актив с нормой наращивания r_A состоят из двух частей: собственного капитала K и займа З, взятого под процент r_З. Инвестор размещает сумму А таким образом, чтобы в конце периода получить плановую процентную маржу

MAR^* = A(1+r _A) – З(1+ r_З) – К = З(r_A – r_З) + K r_A . (1.1.13)

Пусть Pr_A – вероятность утраты актива в конце периода. Тогда ожидаемое значение маржи снижается

MAR = З(r_A – r_З) + K r_A – (К + З) (1+r _A) Pr_A. (1.1.14)

Коэффициент риска (1.1.8) примет вид

L = = (1 + З / К) (1 + r _A) Pr_A. (1.1.15)

Тем самым степень риска L гиперболически убывает с ростом собственных средств К. Однако это достигается за счет снижения рентабельности их использования

MAR / К = (З/K)(r_A – r_З) + r_A – (1 + З/K) (1+r _A) Pr_A. (1.1.16)

Из (1.1.6, 1.1.8) следует, что при MAR < 0 возрастает риск разорения. Этот эффект тем ощутимее, чем строже выполняется условие

З(r_A – r_З) + K r_A < (К + З) (1+r _A) Pr_A или (1.1.17)

(З/K)(r_A – r_З) + r_A < (1 + З/K) (1+r _A) Pr_A .

Из статистики известно (см. модуль 1, стр. 55-56), что дисперсия s_å смеси из N независимых вкладов, каждый из которых имеет дисперсию s, выражается как

s_å = s /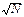. (1.1.18)

Тем самым диверсификация является мощным средством уменьшения риска.

1.2. Управление рисками с использованием функций

полезности доходов и кривых безразличия.

Модифицируя (1.1.10) и переходя к ожидаемой полезности, получают уровневую функцию полезности Неймана-Монгенштерна

L(m, s) = a Mr – bM(r – Mr)² = a m – b s ² . (1.2.1)

В (1.2.1) математическое ожидание m определяет возможный уровень дохода, а дисперсия s – возможный риск. Возможно три вида карт уровней безразличия (к доходам), описываемых уравнениями L(m,s) = C (для разных значений C₁<C₂…<C_K) кривых безразличия (см. рис 1.2.1). Все три карты отражают разный характер отношения к рискам (а – нерасположенность к рискам, б – нейтральность к рискам, в – азарт).

 

 

Рис. 1.2.1

Таблица 1.2.1а
Вероятности	0,2	0,8
Доходность, rA	5%	1,25%
Доходность, rB	-1%	2,75%

Пример 1.2.1. Имеются два актива (A и B) со случайными нормами доходности r_A и r_B. Возможные значения доходности и вероятности исходов показаны в таблице 1.2.1а.

Пусть функция полезности инвестора L = 1,2 r – 0,1r². Необходимо определить оптимальные пропорции a_A и a_B (a_A+a_B =1) смешанного актива (A+B) по критерию ожидаемой полезности и с использованием уровней безразличия.

Запишем ряд распределений случайных доходности и функции полезности смеси в таблице 1.2.1б.

Таблица 1.2.1б

Вероятности	0,2	0,8
Доходность, r	5aA +(–1)(1–aA) = = 6aA – 1	1,25aA +2,75(1–aA) = = 2,75 – 1,5aA
Полезность, L	L1(aA) =1,2 (6aA –1) – – 0,1(6aA –1)2	L2(aA) = 1,2 (2,75–1,5aA) – – 0,1(2,75–1,5aA)2

Соответствующая смеси математическое ожидание будет определяться выражением МL(a_A)=0,2L₁(a_A)+0,8L₂(a_A). Для оптимизации пропорций смеси необходимо найти такое a_A, чтобы

¶ МL(a_A)/¶a_A = 0. (1.2.2)

Отсюда (и на основании таблицы 1.2.1б) получим уравнение

0,2[1,2*6 – 0,2(6a_A–1)6]+0,8[–1,2*1,5–0,2(2,75–1,5a_A)*

*(– 1,5)] = 0 и его решение a_A = 0,5.

Решим ту же задачу, но с использованием уровневой функции полезности (1.2.1). Из таблицы 1.2.1а следует, что

m_A = 0,2*5 + 0,8*1,25 = m _B = 0,2*(–1) + 0,8*2,75 = 2;

s_A² = 0,2*(5–2)² + 0,8*(1,25–2)² =s_B² =

= 0,2*(–1–2)² + 0,8*(2,75–2)² = 2,25; cor_AB = –1

(см. пример 1.1.1, выражение 1.1.5). Отсюда, используя (1.1.12), получим

m_å =a_A m_A +(1 – a_A) m_B = 2;

s_å ²=s_A²(a_A – a_B)²=s_A²(2a_A –1)² =2,25(2a_A –1)².

Подставляя s_å²в(1.2.1) получим следующую задачу максимизации

1,2*2–0,1*2,25(2a_A–1)² 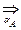max, имеющее решение a_A=0,5.

Использование уровневой функции полезности для управления диверсификацией. Обозначим a_j, j =1, 2, …, J – долю в общем вложении инвестора, приходящуюся на «j-ый» вид актива (например, ценную бумагу) с ожидаемыми доходностью m_j и риском s_j. При случайной доходности r_j каждого вида актива эффективность смеси (портфеля ценных бумаг) определяется выражением

R_å = . (1.2.3)

Математическая модель управления диверсификацией путем двухкритериальной оптимизации (ожидаемых эффективности m и риска s смеси) выглядит следующим образом

m_å = MR_å =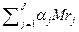=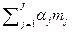Þ max, (1.2.4)

s_å² =M (R_å–m_å)² = Þ min, = 1,

где cor_ij = M[(r_i – m_i)(r_j – m_j)]/s_i s_j – коэффициенты корреляции (взаимной связи) доходностей разных активов (–1 £ cor_ij £ 1).

При операциях с ценными бумагами искомые величины a_j долей вложений могут быть как положительными (покупка), так и отрицательными (продажа).

Решением оптимизационной задачи (1.2.4) является вектор a^* = (a₁^*,a₂^*, …, a_J^*).

Однако следует заметить, что не всегда можно получить решение a^*, оптимизирующее сразу два критерия (m Þ max; s ² Þ min).

Решение, которое не может быть улучшено сразу по двум критериям называется Парето-оптимальным или эффективным.

Двухкритериальную оптимизацию сводят к пошаговой однокритериальной (задаче оптимизации Т. Марковица), выполняя следующие этапы:

1) Ищут такое решение a, которое доставляет минимум ожидаемому риску s при условии, что обеспечивается заданное значение m ожидаемой эффективности при бюджетном балансе åa_j = 1.

2) Изменяют заданное значение m ожидаемой эффективности и снова выполняют пункт 1, находя таким образом множество {a} допустимых решений и соответствующее ему множество {s} ожидаемых рисков. Найденное множество {s} отображается на плоскости {s, m} эффективной траекторией (рис. 1.2.2а).

 

 

Рис. 1.2.2

3) На плоскости {s, m} строят кривые безразличия L(m,s,a) = C уровневой функции L(m,s,a) полезности смеси. Парето-оптимальное эффективное решение a^* и соответствующие оптимальные доход m_B и риск s_B находят для функции полезности, кривая безразличия которой касается эффективной траектории {s} в одной точке B.

Диверсификация с безрисковой компонентой. В случае вложения средств в активы с гарантированной (безрисковой) доходностью r₀ с пропорцией a₀ рассмотренная однокритериальная оптимизационная задача управления выглядит следующим образом

min{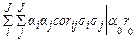+= m, a₀ += 1}.(1.2.5)

Читается как: найти минимум первого выражения при условиях, заданных двумя последующими (после знака “ú ”).

Пример 1.2.2. Рассмотрим пошаговую однокритериальную оптимизационную задачу диверсификации по двум рисковым активам (m₁,s₁) < (m₂,s₂)

s ² =a₁²s₁² +2a₁a₂ cor₁₂ s₁s₂ + a₂²s₂² Þ min, (1.2.6)

m =a₁ m₁ + a₂ m₂, a₁ + a₂ = 1.

Как показано на рис. 1.2.3а при каждом заданном значении m (ожидаемой доходности смеси) получается единственное допустимое решение a_A = (a_1A,a_2A), определяемое точкой A пересечения линий уравнений ограничений (m=a₁ m₁+a₂ m₂ и a₁+a₂ = = 1).

При движении линии уравнения ограничения (m=a₁m₁+a₂m₂) в сторону роста m можно выйти на множество допустимых решений {a_A} со сколь угодно высоким уровнем ожидаемой доходности смеси, что естественно достигается с помощью, так называемых, коротких продаж по первому активу (a₁ < 0, a₂ > 0). При ограничении на знаки вкладов (a₁ >0, a₂ >0) уровень ожидаемой доходности смеси будет ограничен: m₁ £ m £ m₂.

 

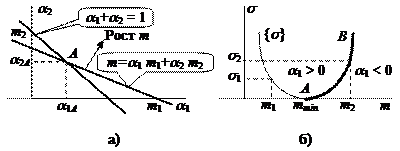Рис. 1.2.3

Исключая в (1.2.6) a₂, получим

m = m₂ – a₁ (m₂ – m₁), (1.2.7)

s ²(m) =

=.

Отсюда следует, что s (m₁) = s₁, s (m₂) = s₂.

Построим график допустимых решений. Для этого, исходя из уравнения

¶s ²(m)/¶m = (1.2.8)

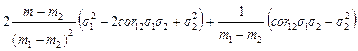== 0,

найдем минимальное значение s_min риска и соответствующую ему доходность m_min

m_min = 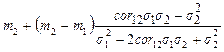, (1.2.9)

s ²_min = .

Из (1.2.9) следует, что нулевой риск s _min = 0 достигается в случае полной корреляции, т.е., когда cor₁₂ = ±1. Для cor₁₂ = –1 экономический смысл нулевого риска был рассмотрен ранее (см. 1.1.12). Для cor₁₂ = 1 безрисковые вклады можно получить, сочетая закупки одного из активов с короткими продажами другого.

На основании (1.2.7) легко построить уравнение траектории (рис. 1.2.3б) для множества допустимых решений с эффективной частью AB («жирная» линия).

Подставим в уравнение am – bs ² = C (кривой безразличия) правую часть выражения (1.2.7), и из уравнения ¶C/¶ m = 0 найдем точку m = m_B, доставляющую максимум C

m_B = (1.2.10)

= .

Тогда из (1.2.7) получим

a₁ =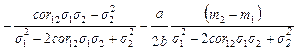.(1.2.11)

Пример 1.2.3. Рассмотрим пошаговую однокритериальную оптимизационную задачу диверсификации (1.2.5) при рисковом (m₁, s₁) и безрисковом (r₀ < m₁) активах

min{s = (1–a₀)s₁ú m = a₀ r₀ +(1–a₀) m₁, a₀ +a₁ = 1, a₁ ³ 0}.

Исключая из целевого критерия a₀, получим линейную связь между риском и эффективностью

s = ½½s₁, (1.2.12)

отображаемую восходящей прямой (рис. 1.2.4).

 

 

Рис. 1.2.4 Рис. 1.2.5

Очевидно, что все сочетания активов, представленные точками луча АС, являются Парето-оптимальными. Часть AB траектории относится к случаю отсутствия заемного капитала (a₀ ³ 0). Часть BC траектории соответствует росту риска при взятии заема (a₀ < 0).

Из множества эффективных решений выберем такие, которые удовлетворяют эквивалентным оптимизационным уравнениям

{a[a₀ r₀ +(1–a₀)m₁] – b[(1–a₀)²s₁²]}, или (1.2.13)

{am – b[(m – r₀)/(m₁ – r₀)]²s₁²}.

Из любого уравнения получим оптимальное решение

a₀ = 1 – (a/2b)(m₁ – r₀)/ s₁², (1.2.14)

которое естественно является частным случаем (1.2.11), если в нем учесть соответствующую безрисковою компоненту.

Общий случай пошаговой однокритериальной оптимизации при добавлении безрисковых компонентов к рисковым активам. Примеры 1.2.2 и 1.2.3 показывают, что при диверсификации возможно сочетать рисковые и безрисковые вклады. В общем случае графическое решение задачи (1.2.5) показано на рис. 1.2.5.

Здесь допустимое множество решений представлено кривой ABE, полученной касанием кривой AC, описывающей безрисковое вложение в соответствии с примером 1.2.3, и кривой DBE, описывающей допустимые решения, оптимизирующие риски при заданном уровне эффективности в соответствии с примером 1.4.2. Паретто-оптимальное решение a^*, минимизирующее риски и соответствующее оптимальному сочетанию рискового и безрискового вложений, находится и в точке B касания. При операциях с ценными бумагами портфель a^*, соответствующий данной точке B, называют оптимальным портфелем.

Пример 1.2.4. Найдем оптимальный портфель из двух рисковых ценных бумаг с характеристиками m₁ = 2, s₁ = 1; m₂ = 3, s₂ = 2; cor₁₂ = 0,5 при условии, что эффективность добавляемого безрискового актива составляет r₀ = 1.

Чтобы найти абсциссу m_B точки касания B (см. рис. 1.2.5), запишем уравнение касательной к функции f(x) в точке x₀

y(x) = f(x₀) + f ^’(x₀) (x – x₀) (1.2.15)

Используя (1.2.7) и (1.2.8), получим уравнение касательной в точке B

s(m) =

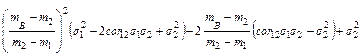= []^1/2 +

+[]^-1/2 *

* [] *

* (m – m_B). (1.2.16)

В соответствии с рис. 1.2.5 данная прямая «отсекает» на оси абсцисс точку A = {m_A = r₀ = 1, s(r₀) = 0}. Подставляя координаты точки A в (1.2.16), получим общий вид доходности m_B оптимального портфеля с безрисковой компонентой

m_B = [m₂(m₂ – r₀)(s₁² – 2cor₁₂s₁s₂+s₂²) + (1.2.17)

+ (m₂ – m₁)(2m₂ – r₀)(cor₁₂s₁s₂ – s₂²) +s₂²]/

/[(m₂ – r₀) (s₁² – 2cor₁₂s₁s₂ + s₂²)+(m₂ – m₁)(cor₁₂s₁s₂ –s₂²)],

Поскольку для рисковых вкладов справедливо

m = a₁ m₁ + (1 – a₁)m₂, то (1.2.18)

a₁ = (m₂ – m_B)/(m₂ – m₁) = [(m₂ – r₀) (m₂ – m₁)(s₂² – cor₁₂s₁s₂) –s₂²]/

/[(m₂ – r₀)(m₂ – m₁)(s₁²–2cor₁₂s₁s₂s₂²) + (m₂–m₁)²( cor₁₂s₁s₂–s₂²)].

Для заданных значений примера из (1.2.17) и (1.2.18) получим m_B = 7/3, a₁ = 2/3, a₂ = 1/3.

Рассмотренный пример обобщает теорему об инвестировании в два фонда, утверждающую, что каждый инвестор, интересующийся только ожидаемыми доходностью и риском-отклонением, будет комплектовать портфель только из «касательного» (оптимального) и безрискового активов.

1.3. Управление рисками на основе их нечетких

параметрических характеристик.

Нечеткие риски и их параметрические характеристики могут быть охарактеризованы следующим примером. Некто имеет единичный капитал и вкладывает его в рублевый и валютный банки с процентными ставками r_Р и r_B соответственно. Предположим, что валютный курс (отношение доллара к рублю) вначале периода K₀, а в конце не определен и задан некоторым коридором возможных значений

K₁ Î [K_1a , K_1b]. (1.3.1)

Наращенная сумма к концу периода будет в соответствии с (1.1.3, модуль 2, стр. 7) равна

S = a_Р(1+r_Р) + (1–a_Р) (1+r_B) K₁/K₀, (1.3.2)

где a_Р – доля рублевого вложения. Возможны два предельных случая рисков в виде величин условных потерь (при a_Р = 1 и a_Р = 0 соответственно)

D_Р(a_РúK₁) = (1+ r_A) – S = (1.3.3)

= (1–a_Р) [K₀ (1+r _Р) – K₁ (1+r_B)]/K₀,

D_B(a_РúK₁) = (1+r_B) (K₁/K₀) – S = a _Р[K₁ (1+r_B) – K₀ (1+r _Р)]/K₀.

Очевидно, что максимальные значения эти риски приобретают на концах заданного интервала [K_1a , K_1b]. Предположим, что осторожный вкладчик, желающий обеспечить себе твердый доход, придерживается критерия минимизации наибольшего из двух рисков D _Р(a_РúK_1a) и D_B(a_РúK_1b). Математически это означает, что решается следующая минимаксная задача

max {D _Р(a_РúK_1a) , D_B(a_РúK_1b)}. (1.3.4)

Данную задачу проще всего решать графически (см. рис. 1.3.1). Из рисунка видно, что решение минимаксной задачи эквивалентно решению уравнения

 

 

Рис. 1.3.1

 

(1–a_{Р opt}) [K₀ (1+r _Р) – K_1a (1+r_B)] = (1.3.5)

= a _{Р opt} [K_1b (1+r_B) – K₀ (1+r _Р)],

из которого следует, что оптимальная пропорция вклада соответствует значению

a_{Р opt} = [K₀ (1+r_Р) – K_1a (1+r_B)]/(1+r_B) (K_1b – K_1a). (1.3.6)

Минимальный риск при этом составит величину

D_min = [K₀ (1+r_Р) – K_1a (1+r_B)] [K_1b (1+r_B) – K₀ (1+r_Р)]/ (1.3.7)

/(1+r_B) K₀ (K_1b – K_1a).

На практике при управлении рисками широко используют как рассмотренные минимаксные критерии, так и вероятностное описание рисков.