Равноточные наблюдения
Статистическое (выборочное) среднее или статистическое математическое ожидание случайной величины находится по формуле
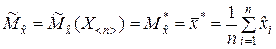 . (5.1.1)
. (5.1.1)
Поскольку наблюдения равноточны, то случайные величины 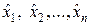 по существу представляют собой «экземпляры» одной и той же случайной величины
по существу представляют собой «экземпляры» одной и той же случайной величины 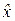 и, следовательно, имеют один и тот же закон распределения с числовыми характеристиками:
и, следовательно, имеют один и тот же закон распределения с числовыми характеристиками:
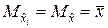 ;
; 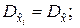
 ,
,  .
.
Покажем, что оценка 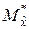 удовлетворяет всем трём общим требованиям.
удовлетворяет всем трём общим требованиям.
1. Из выражения (5.1.1) следует, что
 .
.
Таким образом, 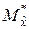 является несмещённой оценкой параметра
является несмещённой оценкой параметра 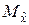 .
.
2. Согласно теореме Чебышева среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к её математическому ожиданию
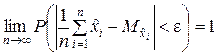 .
.
Следовательно, статистическое среднее 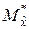 есть состоятельная оценка параметра
есть состоятельная оценка параметра 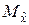 .
.
3. Согласно выражению (5.1.1) дисперсия статистического среднего
 (5.1.2)
(5.1.2)
с ростом объёма n выборки неограниченно убывает и, следовательно, 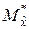 асимптотически эффективная оценка
асимптотически эффективная оценка 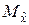 . Доказано, что если случайная величина
. Доказано, что если случайная величина 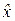 подчинена нормальному закону распределения, то при любых n дисперсия (5.1.2) будет минимально возможной. В таком случае
подчинена нормальному закону распределения, то при любых n дисперсия (5.1.2) будет минимально возможной. В таком случае 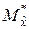 является эффективной оценкой математического ожидания
является эффективной оценкой математического ожидания 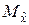 .
.
Следовательно, 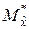 – это подходящее значение
– это подходящее значение 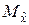 :
:
 . (5.1.3)
. (5.1.3)
П р и м е р 5.1. В условиях примера 4.1 найти оценку математического ожидания случайной величины  .
.
▼ Согласно формуле (5.1.3)
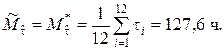
Случайная выборка, приведённая в табл.4.3, была получена при наблюдении случайной величины  , математическое ожидание которой
, математическое ожидание которой  Сравнительно невысокая точность полученной оценки обусловлена малым объёмом выборки, но ни в коей мере не способом её вычисления. ▲
Сравнительно невысокая точность полученной оценки обусловлена малым объёмом выборки, но ни в коей мере не способом её вычисления. ▲
Если объём n выборки достаточно велик, то вычисления по формуле (5.1.3) оказываются громоздкими. Задачу можно упростить, если использовать данные интервального вариационного ряда, т.е. полагать
 , (5.1.4)
, (5.1.4)
где  – представитель (середина) l-го разряда вариационного ряда;
– представитель (середина) l-го разряда вариационного ряда; 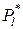 – частота попадания вариантов xi случайной величины
– частота попадания вариантов xi случайной величины 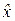 в l-й разряд.
в l-й разряд.
Значение оценки 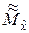 , определяемое по формуле (5.1.4), оказывается приближённым, однако с ростом n (а, следовательно, и r) точность данной формулы возрастает.
, определяемое по формуле (5.1.4), оказывается приближённым, однако с ростом n (а, следовательно, и r) точность данной формулы возрастает.
П р и м е р 5.2. В условиях примера 4.2 найти приближённое значение оценки  математического ожидания
математического ожидания  случайной величины
случайной величины 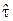 .
.
▼ Используем данные табл.4.7. По формуле (5.1.4) получим
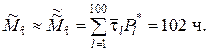 ,
,
▲
Следует обратить внимание на то, что выборка, приведённая в табл.4.7, принадлежит той же генеральной совокупности, что и в табл.4.3. Однако, как видно из решений примеров 5.1 и 5.2, в последнем случае даже приближённое значение оценки  меньше отличается от истинного значения параметра
меньше отличается от истинного значения параметра  = 100 ч. Это объясняется бо́льшим объёмом n и, следовательно, большей информативностью выборки, приведённой в табл.4.7.
= 100 ч. Это объясняется бо́льшим объёмом n и, следовательно, большей информативностью выборки, приведённой в табл.4.7.