Неравноточные наблюдения
Пусть характеристики точности наблюдений от опыта к опыту изменяются так, что наблюдаемая в i-м опыте случайная величина 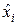 имеет дисперсию
имеет дисперсию
 ,
,  .
.
При этом среднее значение случайной величины 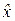 от опыта к опыту не изменяется:
от опыта к опыту не изменяется:
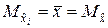 ,
,  .
.
В данном случае оценка  математического ожидания случайной величины
математического ожидания случайной величины 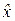 по-прежнему будет являться функцией случайной выборки:
по-прежнему будет являться функцией случайной выборки:
 .
.
Необходимо так выбрать вид этой зависимости, чтобы оценка имела простое аналитическое выражение и была несмещённой, состоятельной и эффективной.
Так как наиболее простой функциональной зависимостью является линейная, то будем искать оценку  в классе линейных функций:
в классе линейных функций:
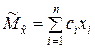 . (5.1.5)
. (5.1.5)
Очевидно, что теперь решение поставленной задачи состоит в отыскании значений коэффициентов ci,  линейной формы (5.1.5), при которых оценка
линейной формы (5.1.5), при которых оценка  будет удовлетворять всем трём указанным выше требованиям.
будет удовлетворять всем трём указанным выше требованиям.
1. Чтобы оценка была несмещённой, должно выполняться равенство
 .
.
Поскольку в этом случае
 ,
,
то коэффициенты ci должны удовлетворять условию
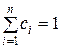 .
.
2. Для того чтобы оценка  была эффективной, её дисперсия
была эффективной, её дисперсия
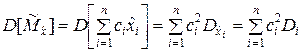 (5.1.6)
(5.1.6)
должна быть минимальной при условии, что
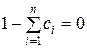 . (5.1.7)
. (5.1.7)
Условный экстремум (минимум) функции (5.1.6) с переменными c1, c2,…, cn отыскиваем методом неопределённых множителей Лагранжа. При этом учитываем, что должно выполняться равенство (5.1.7). Следовательно, исследуем на минимум вспомогательную функцию
 ,
,
где l – неопределённый множитель Лагранжа.
Решаем систему n уравнений
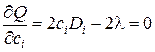 ,
, 
относительно переменных c1, c2,…, cn и получаем
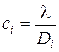 .
.
Таким образом, вес ci, с которым должен входить результат i-го наблюдения в формулу для оценки  , должен быть обратно пропорционален его дисперсии. Иными словами, чем точнее наблюдение, тем с бо́льшим весом необходимо учитывать его результат. Вывод, полученный формально, полностью согласуется с вербальными рассуждениями: чем точнее наблюдение, тем больше ему следует доверять.
, должен быть обратно пропорционален его дисперсии. Иными словами, чем точнее наблюдение, тем с бо́льшим весом необходимо учитывать его результат. Вывод, полученный формально, полностью согласуется с вербальными рассуждениями: чем точнее наблюдение, тем больше ему следует доверять.
Поскольку 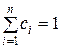 , то
, то  и, следовательно,
и, следовательно,
 . (5.1.8)
. (5.1.8)
Обозначим 1/Di = di, тогда (5.1.8) представляется как 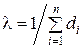 и
и
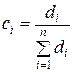 ,
,  . (5.1.9)
. (5.1.9)
Таким образом, выражение для оценки (5.1.5) будет иметь вид
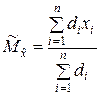 . (5.1.10)
. (5.1.10)
Оценка вида (5.1.10) является эффективной, так как получена на основе требования минимума дисперсии.
3. Минимальная дисперсия несмещённой оценки 
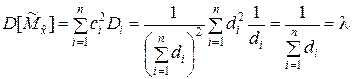 , (5.1.11)
, (5.1.11)
а её среднее квадратическое отклонение
 .
.
Поскольку di = 1/Di = const,  , то из выражения (5.1.11) вытекает, что при неограниченном возрастании количества наблюдений l ® 0. Следовательно,
, то из выражения (5.1.11) вытекает, что при неограниченном возрастании количества наблюдений l ® 0. Следовательно,  сходится по вероятности к
сходится по вероятности к 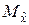 , т.е. является состоятельной оценкой математического ожидания
, т.е. является состоятельной оценкой математического ожидания 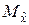 .
.
Частный случай. Предположим, что все наблюдения равноточны. Это означает, что  ,
, 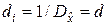 ,
,  ,
,  и тогда
и тогда
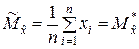
Получим результат как и в пп.5.1.1 – оценкой математического ожидания случайной величины 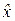 является её статистическое среднее
является её статистическое среднее 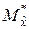 .
.
П р и м е р 5.3. Дальность 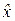 до центра масс ракеты измеряется тремя методами, точность которых характеризуется средними квадратическими отклонениями
до центра масс ракеты измеряется тремя методами, точность которых характеризуется средними квадратическими отклонениями  = 0,2 км,
= 0,2 км,  = 0,5 км,
= 0,5 км, 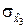 = 1 км. Измерения дальности
= 1 км. Измерения дальности 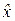 этими методами дали следующие результаты: x1 = 10,0 км; x2 = 9,5 км; x3 = 10,8 км.
этими методами дали следующие результаты: x1 = 10,0 км; x2 = 9,5 км; x3 = 10,8 км.
Найти оценку  математического ожидания
математического ожидания 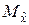 дальности
дальности 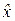 и среднее квадратическое отклонение
и среднее квадратическое отклонение 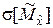 этой оценки.
этой оценки.
▼ По условию задачи
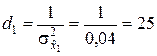 ,
, 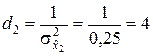 ,
,  .
.
Далее согласно равенствам (5.1.9)
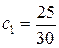 ,
,  ,
, 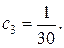
По формуле (5.1.5) получаем
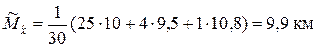 .
.
В соответствии с выражением (5.1.11)
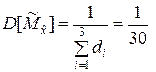 км2,
км2,  .
.
▲