Качество оценивания дисперсии
Качество оценивания дисперсии 
характеризуется доверительным интервалом
и доверительной вероятностью
.
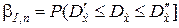При оценивании дисперсии различают случаи известного и неизвестного математического ожидания (см. пп. 5.2.1, 5.2.2). Рассмотрим второй, наиболее распространённый случай. При неизвестном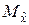 
состоятельная, несмещённая и асимптотически эффективная оценка дисперсии определяется равенством (5.2.9).
При достаточно большом объёме выборки распределение оценки (5.2.9) будет близким к нормальному с параметрами (5.2.10). Следовательно, доверительная вероятность для дисперсии будет приближённо определяться соотношением
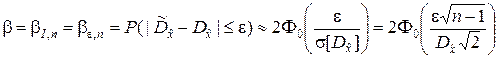, (5.2.15)
где e = eb,n – максимальная с вероятностью b абсолютная погрешность оценки 
дисперсии .
Выражаем e из уравнения (5.2.15) и в результате получим
, (5.2.16)
откуда доверительный интервал
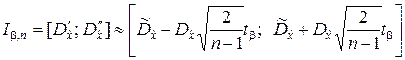. (5.2.17)
Выражения (5.2.15) – (5.2.17) были получены в предположении, что дисперсия известна. В действительности известна лишь её оценка , которая только и может фигурировать в этих формулах. С учётом сказанного будем иметь
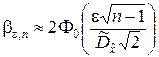; (5.2.18)
; (5.2.19)
. (5.2.20)
Как видно из выражения (5.2.20), доверительный интервал для дисперсии оказывается симметричным относительно оценки . При этом его ширина зависит от значения (рис.5.2).
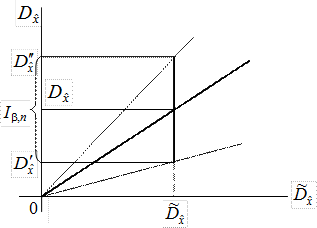
Рис.5.2. Доверительный интервал для дисперсии
Потребный объём экспериментальных данных для оценивания дисперсии с заданными точностью и надёжностью получим, если выразить n из уравнения (5.2.15):
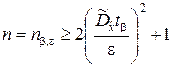, (5.2.21)
Следует отметить, что n определяется, когда дисперсия ещё только подлежит оцениванию. Но значения и вероятностные характеристики оценки , входящей в выражение (5.2.21), зависят от объёма выборки. Поэтому объём n определяется методом последовательных приближений. В первом приближении задаются некоторым ориентировочным значением n0, при котором вычисляется приближение 
оценки . Затем оно уточняется в последующих циклах вычислений. Очевидно, что если n0 превышает найденное по формуле (5.2.21) значение n, то принимается n = n0. В данном случае оценка = уже удовлетворяет требованиям по точности и надёжности.
П р и м е р 5.8. В условиях примера 5.6:
1) найти приближённое значение числовых характеристик дисперсии случайной величины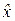 
;
2) построить 80-процентный доверительный интервал для дисперсии;
3) определить доверительную вероятность b для дисперсии, если максимальная с вероятностью b погрешность eb = 0,02.
▼ 1. По формулам (5.2.10) получаем:
; 
;
.
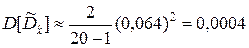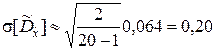2. Используем выражение (5.2.19):
.
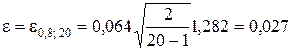Доверительный интервал для дисперсии в соответствии с (5.2.20):
.
3. По формуле (5.2.18)
.
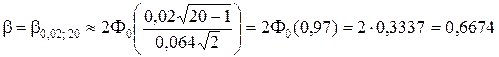Значение F0(x) найдено в приложении 2.
▲