Экзамен гр. 674
Задача 1.
Известно эмпирическое распределение:
| Границы интервалов | Частота попадания в полуинтервал |
| 10-15 | |
| 15-20 | |
| 20-25 | |
| 25-30 |
Найти значение 30 % - ного квантиля.
▼
Формула квантиля:
Ха = Хl-1 + ∆*(а-Fl-1)/wl, где l-тый интервал квантильный, то есть Fl-1 < а < Fl
∆ - длина интервала (5)
Fl-1 – значение эмпирической функции распределения на левой границе l-того полуинтервала, равна сумме всех частот до l-того полуинтервала (не включительно) делённой на число элементов в выборке.
wl – частота попадания в l-тый полуинтервал, делённая на число элементов в выборке, доля наблюдений, попавших в l – тый полуинтервал в общем числе наблюдений
30 % -тный квантиль значит отделяющий ≈ треть выборки. Вся выборка = 10 (∑ всех частот) Þ квантиль отделяет ≈ 3 числа выборки Þ квантильный полуинтервал второй (15-20).
Fl-1 = 1/10 = 0.1; а=0.3; Хl-1 = 15; wl = 3/10 = 0.3
Подставив в формулу получим: Ха = 15 + 5*(0.3-0.1)/0.3 = 15 + 10/3 ≈ 18.33
▲
Задача 2.
Случайная величина измерена три раза в неизменных условиях. полученные значения: 45,50,55. Найти интервальную оценку истинного значения этой величины с уровнем доверия 95%, если известны значения квантилей распределения Стьюдента.
| Степени свободы | |||
| Квантили | 12.7 | 4.3 | 3.18 |
▼
Цель: построить доверительный интервал.
Оценка истинного значения b= Хср = 50. σ2b=σ2х / N = ∑(хi-хср)2 / (N-1)*N , где σ2х – несмещённая оценка дисперсии единичного наблюдения.
σ2х = 52 + 52 /3-1 = 25; σ2b = 25/3
Интервал: b ± tN-n-1,q √σ2b = b ± tN-n-1,q √σ2х / N, где tN-n-1,q – двух сторонний q-процентный квантиль распределения Стьюдента.
Имеем: 50 ± 5*4.3√3 = 50 ± 21.5/√3
(37.59; 62.41)
▲
Задача 3.
Стандартная ошибка измерения труда и капитала составляет 1%, ошибки измерений не скоррелированы. Найти относительную ошибку объёма продукции, рассчитанного по производственной функции Кобба-Дугласа: У=СКαLβ.
▼
Относительная ошибка = коэфициент вариации = σ/хср.
Значит нам надо найти σу/уср = σу/у (так как у нас одно измерение Þ уср = у)
По формуле σ2у = ▼У′ * Ω * ▼У, где Ω – матрица ковариаций величин К и L, а ▼У – градиент функции У.
▼У′ = [αСКα-1Lβ; βС КαLβ-1]
| Ω | σ2К | соν (К,L)=0 |
| соν (L,К)=0 | σ2L |
[αСКα-1Lβ * σ2К] *[αСКα-1Lβ]
σ2у =▼У′*Ω*▼У= [βСКαLβ-1 * σ2L] *[βСКαLβ-1] = α2С2К2α-2L2β * σ2К + β2С2L2β-2К2α * σ2L
Поделим σ2у на у2 = С2К2αL2β Þ получим σ2у / у2 = α2 σ2К /К2 + β2σ2L / L2 . Учитывая что стандартная ошибка измерения труда и капитала – это коэффициент вариации и учитывая что Кср =К и Lср =L (так как только одно измерение) Þ σ2К /К2 = (σК /К)2 = (0.01)2 =(σL /L)2 = σ2L /L2 Þ
σ2у / у2 = α2*(0.01)2 + β2*(0.01)2 Þ σу / у = 0.01√α2 + β2
▲
Задача 4.
Дисперсии двух переменных совпадают, корреляция отсутствует. изобразить на графике в пространстве переменных линии прямой, обратной и ортогональной регрессии. Ответ обосновать.
У=аХ + b – прямая регрессия
а=mху/mхх, где mху –ковариация случайных величин х и у; mхх –дисперсия случайной величины х
а=0/mхх=0, все линии регрессий проходят через точку (хср,уср) Þ b=хср.
а=0=tg угла наклона линии прямой регрессии Þ угол наклона равен 0 градусов.
Х=сУ + d –обратная регрессия
с = mху/mуу, где mуу –дисперсия случайной величины у
с = 0/ mуу=0
Преобразуем уравнение обратной регрессии: У=Х/с –d/с
1/с = ∞ =tg угла наклона Þ угол наклона равен 90 градусов
а2У + а1Х = B – ортогональная регрессия
преобразуем: У = -(а1/а2)*Х + B/а2
По формуле -(а1/а2) = {mуу – mхх + √[(mхх-mуу)2 + 4m2ху] } / 2mху
Учитывая что mуу = mхх & mху = 0. Получим -(а1/а2) = 0/0 – то есть угол наклона линии ортогональной регрессии неопределён Þ ортогональная регрессия – это любая прямая, проходящая через точку (хср,уср).
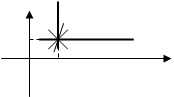 обратная
обратная
ортогональные
уср прямая
хср
▲
Задача 5.
| Может ли матрица Ω = | являться ковариационной матрицей переменных, для которых строится уравнение регрессии. Ответ обосновать. | ||
▼
Из данных следует что mху=3, mхх=2, mуу=4.
Найдём коэффициент детерминации по формуле: R2 = m2ху/mхх*mуу = 9/8 > 1 – невозможно так как R2 Î[0;1]
▲
Задача 6.
Что показывает уровень значимости оценок коэффициентов регрессии.
▼
Уровень значимости –ошибка первого рода - это вероятность с которой наш критерий отвергнет гипотезу о незначимости фактора, при условии, что в действительности фактор был незначим (т.е. гипотеза была верна).
▲
Задача 7.
В каком случае применяется обобщённый метод наименьших квадратов.
▼
В случае когда матрица ковариаций остатков имеет вид σ2Ω, где Ω – отлична от I (единичной матрицы) и Ω – известна.
▲
Задача 8.
Пятифакторное уравнение линейной регрессии для переменной У оценено по 31 наблюдению. при этом объяснённая и остаточная дисперсия равны соответственно 8 и 2. Вычислить коэффициент детерминации и расчетное значение F статистики.
▼
По формуле R2 = 1 – σ2Е/ σ2х, где σ2Е - остаточная дисперсия σ2х – сумма остаточной и объясненной дисперсии (суммарная дисперсия).
R2 =1 –2/(8+2)= 0.8
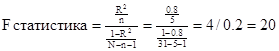
▲
Задача 9.
В регрессионное уравнение, объясняющее оценки, полученный студентами на экзамене, введено 2 качественных фактора: пол (м,ж) и группа (I,II). Полученные оценки параметров при соответствующих фиктивных переменных 0.3 и -0.3 – для первого фактора и 0.1 и –0.1 для второго фактора. Взаимодействие факторов оказалось несущественным, кто наиболее успешно сдаст экзамен.
▼
Учитывая что качественные переменные входят в свободный член, получаем: наличие положительного коэффициента перед фиктивной переменной увеличивает свободный член а следовательно и объясняемую переменную (оценки) по сравнению с отрицательным коэффициентом, значит лучше всех сдадут парни первой группы.
▲