Автокорреляционная функция
Из (3) и (5) получаем
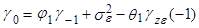 (7)
(7)
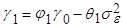 (8)
(8)
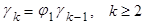 (9)
(9)
Действительно, умножая (6) на 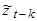 и переходя к математическим ожиданиям, получим:
и переходя к математическим ожиданиям, получим:
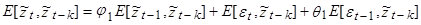
или 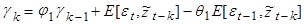 (10)
(10)
При k=0 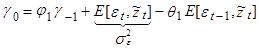
Умножим (6) на 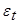 и перейдем к математическим ожиданиям:
и перейдем к математическим ожиданиям:
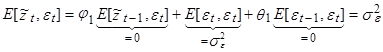
Следовательно, с учетом того, что 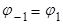 , имеем:
, имеем:
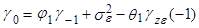 , т.е. подтвердили (7). Далее, подставляя в (10) k=1, имеем
, т.е. подтвердили (7). Далее, подставляя в (10) k=1, имеем 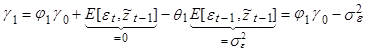
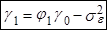 (8)
(8)
И, наконец, 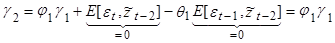 , т.е.
, т.е.
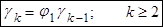 (9)
(9)
Умножив все члены (6) на 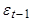 и, переходя к математическим ожиданиям, получим:
и, переходя к математическим ожиданиям, получим:
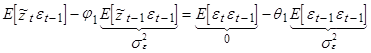
или
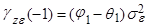 (11)
(11)
Отсюда автоковариационная функция процесса равна:
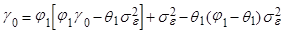
(подстановкой в (7) выражений (8) и (11)) или:
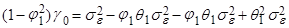
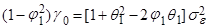
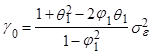 (12)
(12)
Теперь, подставляя в (8) выражение (12), получим:
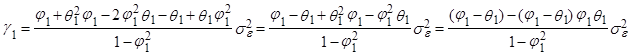
следовательно,
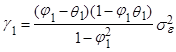 (13)
(13)
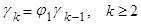 (14)
(14)
Отсюда следует, что автокорреляционная функция экспоненциально убывает от значения 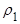 , зависящего от
, зависящего от 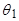 и
и 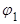 .
.
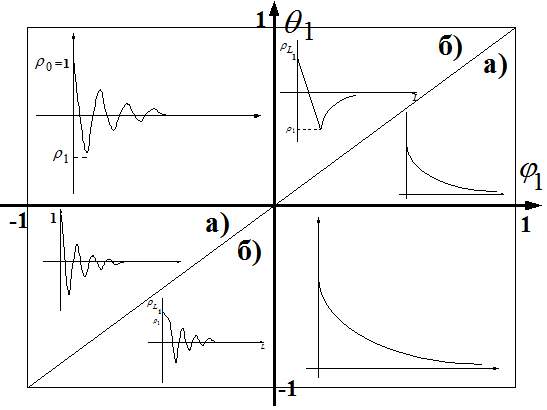
Как показано на рисунке, это затухание монотонное, если 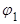 положительно, и колебательное, если
положительно, и колебательное, если 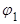 отрицательно.
отрицательно.
Далее, знак 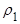 определяется знаком (
определяется знаком (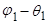 ) и указывает, происходит ли затухание
) и указывает, происходит ли затухание 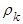 в области положительных или отрицательных значений.
в области положительных или отрицательных значений.
Пользуясь (12), (13), (14) можно вырезать первые две автокорреляции через параметры процесса:
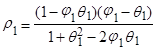 (15)
(15)
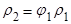 (16)
(16)
Т.к. 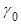 всегда больше нуля, то и
всегда больше нуля, то и 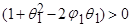 , следовательно знаменатель (15) больше 0, и поскольку
, следовательно знаменатель (15) больше 0, и поскольку 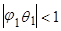 , то
, то 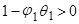 . Знак
. Знак 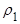 действительно зависит от
действительно зависит от 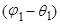 .
.
Знаки последующих 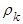 зависят от знака
зависят от знака 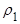 и знака
и знака 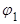 .
.
| Комментарии к рисунку | ||
| I квадрат | а) 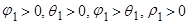
| б) 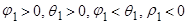
|
| II квадрат | 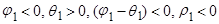
| |
| III квадрат | а) 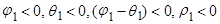
| б) 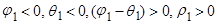
|
| IV квадрат | 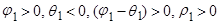
|
Из условий стационарности и обратимости процесса 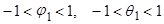 , а также из (15) и (16) вытекает, что
, а также из (15) и (16) вытекает, что 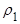 и
и 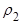 должны лежать в области:
должны лежать в области:
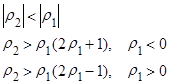 (17)
(17)
Область допустимых значений 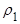 и
и 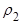 показана на рисунке. Она ограничивает диапазон допустимых комбинаций
показана на рисунке. Она ограничивает диапазон допустимых комбинаций  и
и  для стационарного обратимого процесса АРСС (1,1)
для стационарного обратимого процесса АРСС (1,1)
Действительно, посмотрим во что переходит область допустимых значений, изображенная на следующем рисунке:
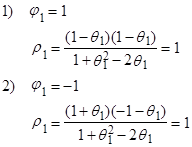
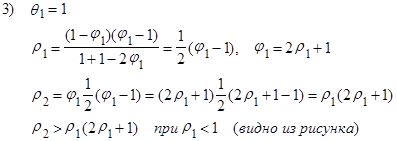
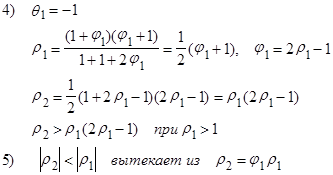
ЛЕКЦИЯ 7
ЛИНЕЙНЫЕ НЕСТАЦИОНАРНЫЕ МОДЕЛИ