ПРОЦЕССЫ СКОЛЬЗЯЩЕГО СРЕДНЕГО
Процесс скользящего среднего порядка q®CC(q) можно записать в виде:
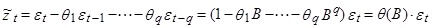 (1)
(1)
Несложно заметить, что т.к. ряд 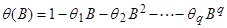 конечен, процесс СС является стационарным без каких-либо ограничений на параметры q.
конечен, процесс СС является стационарным без каких-либо ограничений на параметры q.
Действительно, автоковариационная функция процесса CC(q) равна:
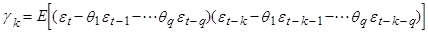
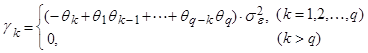 (2)
(2)
Дисперсия процесса равна:
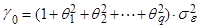 (3)
(3)
Тогда автокорреляционная функция имеет вид:
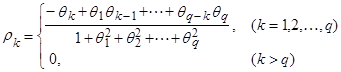 (4)
(4)
Стало быть, дисперсия процесса 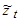 равна дисперсии белого шума
равна дисперсии белого шума 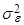 , умноженной на постоянную величину
, умноженной на постоянную величину 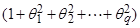 . Значит, процесс стационарен при любых значениях. В справедливости формулы (2) легко убедиться:
. Значит, процесс стационарен при любых значениях. В справедливости формулы (2) легко убедиться:
При k=1 находится (авто)ковариация между рядами:
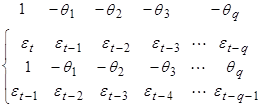
При k=2:
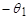
| 
| 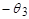
| 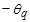
| ||
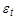
| 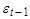
| 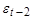
| 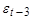
| … | 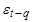
|
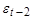
| 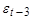
| 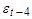
| 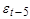
| … | 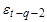
|
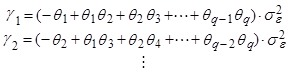
Из выражения (4) мы видим, что автокорреляционная функция процесса CC(q) равна нулю для значений k, больших порядка процесса q. Другими словами, автокорреляционная функция процесса CC(q) обрывается на задержке q. Но для того, чтобы процесс CC(q) обладал свойством, называемым “обратимостью”, на параметры q должны налагаться определенные ограничения.
Для иллюстрации смысла понятия обратимости рассмотрим (как и в лекции 3) модель СС(1):
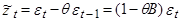 (5)
(5)
Выражая 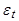 через
через 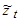 получим:
получим:
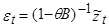 ,
,
т.е.
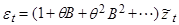 ,
,
или
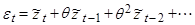 , (
, (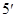 )
)
и выражая 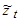 через прошлые значения z, получим:
через прошлые значения z, получим:
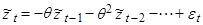 (6)
(6)
Если процесс (5) стационарен при любом q, то процесс (6) стационарен только при 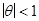 . Действительно, при
. Действительно, при 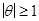 параметры (веса) в разложении (
параметры (веса) в разложении (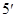 ) образуют расходящийся ряд. Это означает, что текущее значение
) образуют расходящийся ряд. Это означает, что текущее значение 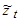 в момент t в (6) зависит от
в момент t в (6) зависит от  с “весами”, растущими по мере увеличения j. Мы избегаем этой ситуации, требуя, чтобы веса в “обращенном” разложении (6) образовывали сходящийся ряд, т.е. чтобы
с “весами”, растущими по мере увеличения j. Мы избегаем этой ситуации, требуя, чтобы веса в “обращенном” разложении (6) образовывали сходящийся ряд, т.е. чтобы 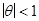 . В этом случае мы будем называть ряд обратимым. Ряд называется обратимым, если веса в “обращенном” разложении образуют сходящийся ряд. Т.е. процесс (5) будет обладать свойством обратимости, если ряд
. В этом случае мы будем называть ряд обратимым. Ряд называется обратимым, если веса в “обращенном” разложении образуют сходящийся ряд. Т.е. процесс (5) будет обладать свойством обратимости, если ряд
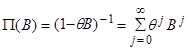 (7)
(7)
сходится. Сходится он при 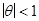 , т.е. в единичном круге. Однако это условие эквивалентно утверждению, что корень характеристического уравнения
, т.е. в единичном круге. Однако это условие эквивалентно утверждению, что корень характеристического уравнения
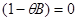 (8)
(8)
лежит вне единичного круга. Действительно, корнем (8) является 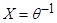 , и т.к.
, и т.к. 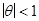 , то
, то 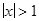 .
.
Аналогично в общем случае. Выведем условия, которым должны удовлетворять параметры 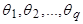 процесса СС(q):
процесса СС(q):
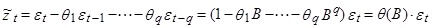 (
(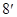 )
)
чтобы этот процесс был обратимым. Условия обратимости могут быть получены, если записать (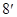 ) как
) как
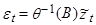
Отсюда, если
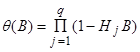 , (9)
, (9)
где 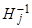 - корни характеристического уравнения
- корни характеристического уравнения 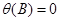 , то
, то  можно разложить на частные дроби:
можно разложить на частные дроби:
 , (10)
, (10)
где 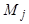 - коэффициенты, которые для всех B после приведения выражения (10) к общему знаменателю в сумме дают 1, чтобы
- коэффициенты, которые для всех B после приведения выражения (10) к общему знаменателю в сумме дают 1, чтобы
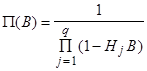 (11)
(11)
Например, для q=2:
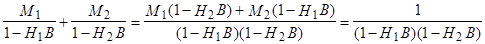
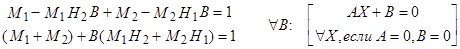
следовательно,
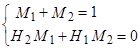
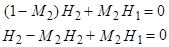
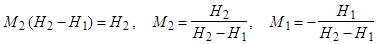
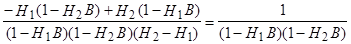
Следовательно, каждое из слагаемых выражения (10) можно, по аналогии с (7), представить в виде бесконечного ряда, который сходится, если 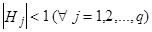 . А т.к. корни характеристического уравнения
. А т.к. корни характеристического уравнения 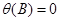 равны
равны 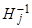 , отсюда следует, что условия обратимости процесса CC(q) состоят в том, что корни характеристического уравнения
, отсюда следует, что условия обратимости процесса CC(q) состоят в том, что корни характеристического уравнения
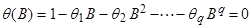
лежат вне единичного круга, т.е. 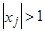 , где
, где 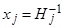 .
.