Теорема Лагранжа и ее следствия
Теорема(Лагранж) (о конечных приращениях). Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется хотя бы одна точка с є (a, b) такая, что выполняется равенство
f(b) – f(a) = f'(с) (b – a) – формула Лагранжа (о конечном приращении).
Доказательство. Теорему Лагранжа можно рассматривать как частный случай теоремы Коши, если положить φ(х) = х. В этом случае
φ(b) – φ(a) = b – a, φ'(x) = 1, φ'(с) = 1.
Подставляя эти значения в формулу  , получаем
, получаем  или f(b) – f(a) = f'(с) (b – a).
или f(b) – f(a) = f'(с) (b – a).
Формула Лагранжа: приращение дифференцируемой функции на отрезке [a, b] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.
Геометрический смысл формулы Лагранжа.
Запишем формулу Лагранжа в виде  , где a < c < b. Отношение
, где a < c < b. Отношение  есть угловой коэффициент секущей АВ, а f'(с) – угловой коэффициент касательной к кривой в точке х = с (рис. 2).
есть угловой коэффициент секущей АВ, а f'(с) – угловой коэффициент касательной к кривой в точке х = с (рис. 2).
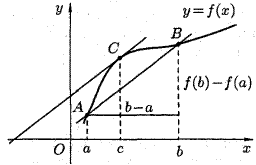
Рис. 2
Следовательно, геометрический смысл теоремы Лагранжа таков: на графике функции f(x) найдется точка С(с, f(с)), в которой касательная к графику f(x) параллельна секущей АВ.
Следствие 1.Если f'(х) = 0 на некотором промежутке (a, b), то функция f(x) постоянна на этом промежутке.
Доказательство. Пусть f'(х) = 0 для любого х є (a, b). Возьмем произвольные х1 и х2 из (a, b) и пусть х1 < х2. Тогда по теореме Лагранжа существует точка с є (a, b) такая, что f(х2) – f(х1) = f'(с) (х2 – х1). Но по условию f'(х) = 0, стало быть, f'(с) = 0, где х1 < с < х2. Поэтому имеем f(х2) – f(х1) = 0 или f(х2) = f(х1). А так как х1 и х2 – произвольные точки из (a, b), то 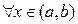 имеем f(x) = с.
имеем f(x) = с.
Следствие 2. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое.
Доказательство. Пусть f'1(х) = f'2(х) при х є (a, b).
Тогда (f1(х) – f2(х))' = f'1(х) – f'2(х) = 0. Следовательно, согласно следствию 1, функция f1(х) – f2(х) есть постоянная, т.е. f1(х) – f2(х) = с для 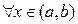 . Теорема доказана.
. Теорема доказана.
Для отрезка [х, х + Δх] формула Лагранжа будет иметь вид:
f(х + Δх) – f(х) = f'(с) Δх.