Момент инерции а.т.т. относительно оси вращения.
Момент инерции а.т.т. (формула (1.41)) является мерой инерции тела при его вращательном движении. Он зависит не только от массы m, но и от ее распределения относительно оси вращения.
Обычно момент инерции тела рассматривают относительно осей проходящих через его центр тяжести. Поэтому, прежде всего выясним, как можно найти его для произвольного тела. Для этого воспользуемся следующим свойством центра тяжести тела: через него проходят оси вращения, относительно которых векторная сумма моментов сил тяжести, действующих на разные части тела, равна нулю.
Рассмотрим в качестве примера сплошной однородный цилиндр. Будем подвешивать цилиндр за разные точки, лежащие на его поверхности, и проводить через них вертикальные линии (рис. 1.16). Тогда в точке их пересечения будет находиться центр тяжести цилиндра (она обозначена утолщенной точкой внутри цилиндра). Такую методику можно применять и для произвольного тела.

Рис.1.16.
Приведем формулы для моментов инерции I тел правильной геометрической формы относительно оси вращения ОО1, проходящей через их центр тяжести так, как показано на рис 1.17.

Рис.1.17.
1. Обруч (или тонкостенный цилиндр) массы m и радиуса r
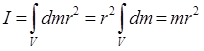 (1.48)
(1.48)
2. Сплошной однородный диск (или цилиндр) массы m, радиуса R и высоты h
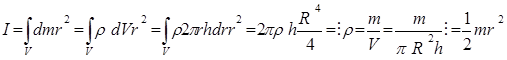 , (1.49)
, (1.49)
где  – плотность материала диска,
– плотность материала диска, 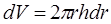 - элементарный объем тела, выбираемый в виде кольцевого слоя радиуса
- элементарный объем тела, выбираемый в виде кольцевого слоя радиуса  толщиной
толщиной  и высоты
и высоты  .
.
3. Однородный шармассы m и радиуса r
 (1.50)
(1.50)
4.Тонкий однородный стержень массы m и длины 
 (1.51)
(1.51)
5. Материальная точка массы m
 ,
,
так как r = 0.
Для расчеты момента инерции тела относительно произвольной оси вращения можно воспользоваться формулой теоремы Штейнера
 , (1.52)
, (1.52)
где – I, I' моменты инерции тела массы m относительно оси, проходящий через центр масс тела (I) и параллельной ей произвольной оси (I'), отстоящей от нее на расстоянии  .
.
Так, для оси  , проходящей через один из концов тонкого стержня (рис. 1.17) можно получить
, проходящей через один из концов тонкого стержня (рис. 1.17) можно получить
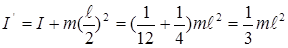 (1.53)
(1.53)
Покажем справедливость теоремы Штейнера на примере тела, состоящего из двух м.т. массы m1 и m2, скрепленных невесомым стержнем . Положение центра тяжести такого тела (точка О) найдем приравняв нулю векторную сумму моментов сил тяжести, действующих на м.т. 1 и 2, относительно оси вращения, проходящей через точку О (ось вращения перпендикулярна плоскости чертежа рис. 1.18)

Рис.1.18.
 ,
, ,
, 
Согласно определению моменты инерции для данного тела относительно осей вращения, проходящих через точки O(I) и O'(I') запишутся таким образом
 ,
, 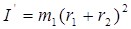
Найдем теперь I' по теореме Штейнера и сопоставим с написанным выше выражение для I'

что и требовалось показать.