Используемые при изложении курса физики.
1. Графический смысл производной от функции y(x) по аргументу x и интеграла от y(x) в пределах значений аргумента от x1 до x2.
Для определения производной функции y по аргументу x при каком-либо значении x = х0 необходимо взять конечные приращения аргумента x
(Δx = x1 - x2) и функции у (Δу = у1 - у2) и затем устремить Δx к нулю, т.е. взять бесконечно малые приращения dх и dу (их также называют элементарными приращениями). Тогда производная у ' будет равна
 (1)
(1)
и графически у ' представляет собой тангенс угла наклона касательной к графику функции в данной точке (рис.1а)
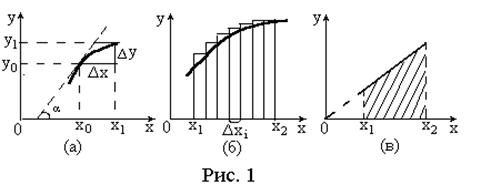
Графически интеграл от функции у в пределах значений аргумента от х1 до х2 представляет собой площадь под графиком функции в пределах от х1 до х2 (рис. 1.б.). Для ее расчета разбивают интервал (х1, х2) на малые участки Δxi(i=1,…,N), определяют площади прямоугольных полосок (уiΔхi) и затем их суммируют..
Точное значение площади под графиком функции получают при стремлении N→ ∞, Δxi→ dx и бесконечная сумма бесконечно малых величин (ydx) обозначается в виде интеграла
 (2)
(2)
Так, в частности, для прямолинейной зависимости у = bx интеграл будет равен площади трапеции (рис. 1.в.) и поэтому

Приведем необходимые для дальнейшего изложения материала ряд формул табличных интегралов
 , (3)
, (3)
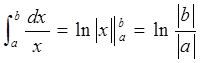 , (4)
, (4)
 , (5)
, (5)
 , (6)
, (6)
2. Скалярное произведение двух векторов  и
и  . Это скалярная величина, равная произведению модулей векторов
. Это скалярная величина, равная произведению модулей векторов  и
и  , умноженного на косинус угла α между ними
, умноженного на косинус угла α между ними
(
 ) = (
) = (
 ) = abcosα = baa ,
) = abcosα = baa ,
где в формулу введена проекция вектора  на направление вектора
на направление вектора 
(ba = bcosα, рис. 2а.).

Скалярное произведение произвольного вектора  на его вектор элементарного приращения d
на его вектор элементарного приращения d можно записать в следующем виде (рис. 2б.)
можно записать в следующем виде (рис. 2б.)
 d
d =
= ,
,
где dc – элементарное приращение модуля вектора  , оно может принимать как положительные, отрицательные, так и нулевые значения. В частности, это относится к элементарным приращениям модулей радиус-вектора
, оно может принимать как положительные, отрицательные, так и нулевые значения. В частности, это относится к элементарным приращениям модулей радиус-вектора 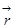 (dr), линейной скорости
(dr), линейной скорости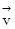 (dv), угловой скорости
(dv), угловой скорости  (dω), и т.д. Для вектора же элементарного углового перемещения
(dω), и т.д. Для вектора же элементарного углового перемещения 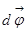 по определению dφ всегда больше нуля.
по определению dφ всегда больше нуля.
3. Векторное произведение векторов  и
и  . Это вектор
. Это вектор , равный по модулю произведению модулей векторов
, равный по модулю произведению модулей векторов  и
и  на синус угла α между ними (рис. 2в.).
на синус угла α между ними (рис. 2в.).
 =[
=[ ´
´ ] , с = ав cosα , α = (
] , с = ав cosα , α = ( ,
, )
)
Вектор  перпендикулярен плоскости вектора
перпендикулярен плоскости вектора  и
и , его направление можно найти по трем эквивалентным правилам: 1) правило правого буравчика. – вращательное движение буравчика должно совпадать с направлением кратчайшего поворота от
, его направление можно найти по трем эквивалентным правилам: 1) правило правого буравчика. – вращательное движение буравчика должно совпадать с направлением кратчайшего поворота от  к
к  , тогда его поступательное движение дает направление
, тогда его поступательное движение дает направление  ; 2) правило левой руки: – четыре пальца нужно расположить по направлению вектора
; 2) правило левой руки: – четыре пальца нужно расположить по направлению вектора  , вектор
, вектор  должен входить в ладонь, тогда отогнутый на 900 большой палец покажет направление
должен входить в ладонь, тогда отогнутый на 900 большой палец покажет направление  ; 3) правило векторного произведения: если смотреть с конца вектора
; 3) правило векторного произведения: если смотреть с конца вектора  на плоскость векторов
на плоскость векторов  и
и  , то тогда кратчайший поворот от
, то тогда кратчайший поворот от  к
к  будет направлен против часовой стрелки.
будет направлен против часовой стрелки.
4. Двойное векторное произведение векторов  ,
, и
и  раскрывается следующим образом
раскрывается следующим образом
[ [
[ ´
´ ]=
]= (
(
 )-
)- (
(
 ) (7)
) (7)
5. Градиент скалярной величины  . Пусть в пространстве каким-либо образом распределена скалярная величина
. Пусть в пространстве каким-либо образом распределена скалярная величина  (существует поле скалярной величины а) – это может быть поле температуры (
(существует поле скалярной величины а) – это может быть поле температуры ( = T), плотности вещества (
= T), плотности вещества ( = ρ), потенциальной энергии (
= ρ), потенциальной энергии ( = Wр) и т.д. Такое поле можно охарактеризовать максимальным и минимальным значением
= Wр) и т.д. Такое поле можно охарактеризовать максимальным и минимальным значением  , средним значением
, средним значением  , а также градиентом
, а также градиентом  . Под градиентом скалярной величины понимают вектор, который в каждой точке пространства направлен в сторону наиболее быстрого возрастания
. Под градиентом скалярной величины понимают вектор, который в каждой точке пространства направлен в сторону наиболее быстрого возрастания  и численно равный приращению величины
и численно равный приращению величины  на единицу длины этого направления
на единицу длины этого направления
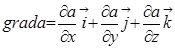 ,
, 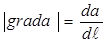 , (8)
, (8)
где  - направление grad
- направление grad в данной точке пространства; вектора
в данной точке пространства; вектора 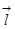 ,
, 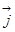 ,
, 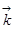 - вектора единичной длины (|
- вектора единичной длины (| |=|
|=| |=|
|=| |), указывающие направления осей Oх, Oу, и Oz в пространстве (рис. 3.). Они позволяют представить произвольный вектор
|), указывающие направления осей Oх, Oу, и Oz в пространстве (рис. 3.). Они позволяют представить произвольный вектор
 в виде суммы его проекции на оси (рис.3)
в виде суммы его проекции на оси (рис.3)
 =
=
 +
+
 +
+
 (9)
(9)
При вычислении производной величины  по координате x в формуле (8) считается, что координаты y и z остаются постоянными – такая производная называется частной производной по координате x
по координате x в формуле (8) считается, что координаты y и z остаются постоянными – такая производная называется частной производной по координате x


Аналогичные предположения принимаются при расчете частных производных по координатам y и z.
Выражение (8) можно записать в более компактном виде, если ввести оператор Гамильтона или оператор Набла
 (10)
(10)
Действие этого оператора на скалярную величину  приводит к выражению (8), т.е. grad
приводит к выражению (8), т.е. grad =
=
 .
.