Непрерывность функции
1.Односторонние пределы функции в точке.
· Правый предел: 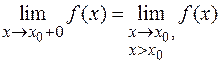 .
.
· Левый предел: 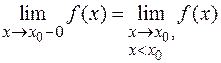 .
.
2.Условия непрерывности функции в точке 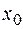 .
.
Функция f(x) непрерывна в точке 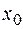 , если она определена в точке
, если она определена в точке 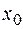 и имеет конечные односторонние пределы в этой точке, причем справедливо равенство:
и имеет конечные односторонние пределы в этой точке, причем справедливо равенство:
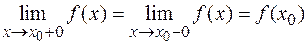 .
.
Если хотя бы одно из условий непрерывности не выполняется, то 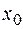 – точка разрыва функции.
– точка разрыва функции.
3.Виды точек разрыва.
В точке 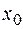 – разрыв 1-го рода, если существуют конечные односторонние пределы функции в точке
– разрыв 1-го рода, если существуют конечные односторонние пределы функции в точке 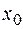 , но они либо не равны между собой, либо не равны значению функции в точке
, но они либо не равны между собой, либо не равны значению функции в точке 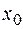 .
.
Причем, разрыв 1-го рода называется:
· неустранимым, если  ;
;
· устранимым, если  .
.
В точке 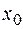 – разрыв 2-ого рода, если хотя бы один из односторонних пределов функции в
– разрыв 2-ого рода, если хотя бы один из односторонних пределов функции в 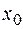 не существует или равен бесконечности.
не существует или равен бесконечности.
4.Свойства и графики основных элементарных функций.
К основным элементарным функциями относятся следующие функции:
· степенные:  ;
;
например: 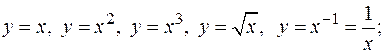
· показательные: 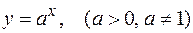 ;
;
например: 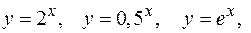 где
где 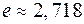 ;
;
· логарифмические: 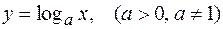 ;
;
например: 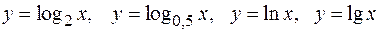 ;
;
· тригонометрические:  ;
;
· обратные тригонометрические: 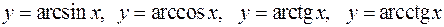 .
.
Графики этих функций приведены в прил. 2.
Отметим, что все основные элементарные функции непрерывны в области их определения.
5.Наиболее часто встречающиеся элементарные функции.
· Линейная функция 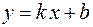 задает прямую линию на плоскости. Ее график можно построить по двум любым выбранным точкам. В частности, линейная функция
задает прямую линию на плоскости. Ее график можно построить по двум любым выбранным точкам. В частности, линейная функция 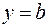 задает на плоскости прямую, параллельную оси
задает на плоскости прямую, параллельную оси  .
.
· Квадратичная функция 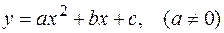 задает параболу. Вершина параболы находится в точке
задает параболу. Вершина параболы находится в точке  ,
,  . Ветви параболы направлены вверх, если
. Ветви параболы направлены вверх, если 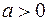 , или вниз, если
, или вниз, если  .
.
Задача. Исследовать на непрерывность функцию в области ее определения. Указать вид точек разрыва, если они имеются. Построить график.
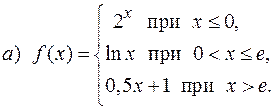
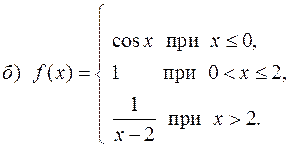
Решение. а) Функция 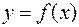 определена при
определена при 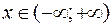 и непрерывна на интервалах
и непрерывна на интервалах  ,
, 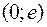 и
и  , так как задана на них основными элементарными функциями.
, так как задана на них основными элементарными функциями.
Исследуем функцию 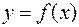 на непрерывность в точках
на непрерывность в точках 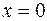 и
и 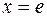 , где происходит смена аналитических выражений функции. Найдем в этих точках односторонние пределы функции.
, где происходит смена аналитических выражений функции. Найдем в этих точках односторонние пределы функции.
При 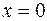 :
: 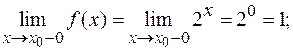
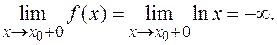
Так как один из односторонних пределов бесконечен, то в точке 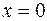 разрыв второго рода.
разрыв второго рода.
При 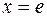 :
: 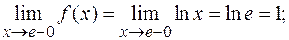
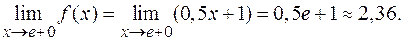
Так как односторонние пределы существуют, но не равны, то в точке 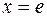 имеется разрыв первого рода, неустранимый.
имеется разрыв первого рода, неустранимый.
Строим график функции (рис. 2).

y
2,5

-1 0 1  3 4 x
3 4 x
-1
Рис. 2.
При 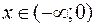 строим график показательной функции
строим график показательной функции 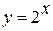 , а при
, а при  – график логарифмической функции
– график логарифмической функции 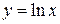 (прил. 2).
(прил. 2).
При 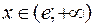 график функции – прямая
график функции – прямая  . Ее удобно строить по двум точкам, например, (3;2,5) и (4;3), так как при
. Ее удобно строить по двум точкам, например, (3;2,5) и (4;3), так как при  ,
, 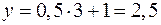 ; при
; при 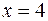 ,
, 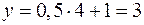 .
.
Ответ.Функция 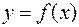 непрерывна во всех точках, кроме точки
непрерывна во всех точках, кроме точки 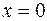 , где имеется разрыв второго рода, и точки
, где имеется разрыв второго рода, и точки 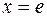 , где имеется разрыв первого рода.
, где имеется разрыв первого рода.
б) 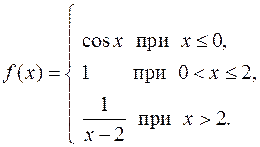
Функция 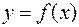 определена при
определена при 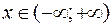 и непрерывна на интервалах
и непрерывна на интервалах  ,
,  , так как задана на них основными элементарными функциями. При
, так как задана на них основными элементарными функциями. При 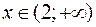
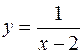 – непрерывна как частное непрерывных функций, где знаменатель
– непрерывна как частное непрерывных функций, где знаменатель  .
.
Исследуем на непрерывность в точках 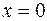 и
и  , где происходит смена аналитических выражений для функции
, где происходит смена аналитических выражений для функции 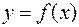 . Найдем в этих точках односторонние пределы функции.
. Найдем в этих точках односторонние пределы функции.
При 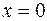 :
: 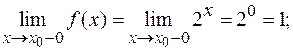
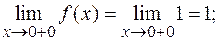

Так как в точке 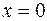 односторонние пределы равны, и они равны значению функции в этой точке
односторонние пределы равны, и они равны значению функции в этой точке  , то функция
, то функция  непрерывна в точке
непрерывна в точке 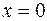 (по определению).
(по определению).
При  :
: 

Так как один из односторонних пределов бесконечен, то в точке  имеется разрыв второго рода.
имеется разрыв второго рода.
Строим график функции (рис. 3).
При 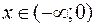 графиком функции
графиком функции 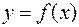 является график тригонометрической функции
является график тригонометрической функции 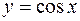 (прил. 2).
(прил. 2).
При 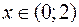 график функции – прямая
график функции – прямая 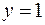 , параллельная оси
, параллельная оси  .
.
При 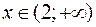 график функции – гипербола
график функции – гипербола 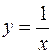 , смещенная на 2 единицы вправо по оси х:
, смещенная на 2 единицы вправо по оси х: 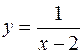 . График строится по нескольким точкам, взятым из указанного промежутка. Например, при
. График строится по нескольким точкам, взятым из указанного промежутка. Например, при 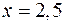 ,
, 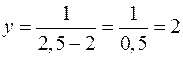 ; при
; при  ,
, 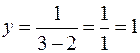 . Таким образом, получены точки графика (2,5;2) и (3;1).
. Таким образом, получены точки графика (2,5;2) и (3;1).
Полезно учесть также, что 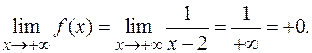

















 y
y
 1
1
-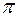

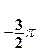

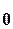

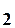

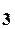 x
x
-1
Рис.3.
Ответ.Функция 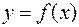 имеет разрыв второго рода в точке
имеет разрыв второго рода в точке  , в остальных точках функция непрерывна.
, в остальных точках функция непрерывна.