Решение
Возьмём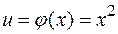 
, тогда 
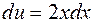и 
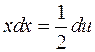. Подставляя это выражение под знак интеграла, получаем:
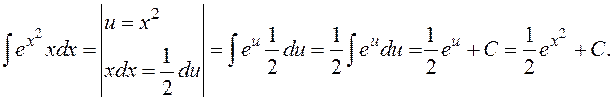
Между двумя вертикальными чёрточками мы записываем сделанные обозначения и комментарии к проделанным преобразованиям.
Метод интегрирования по частям. Пусть функци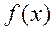и 
и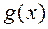 
имеют производную на рассматриваемом интервале изменения 
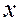. Тогда верно равенство:
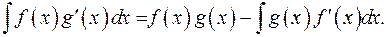
Эта формула называется формулой интегрирования по частям.
Вводя обозначения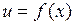 
и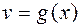 
, замечаем, что 
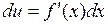и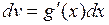 
. Можно записать формулу интегрирования по частям в виде:
.
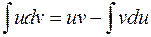Эта формула используется в тех случаях, когда подынтегральная функция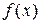 
представляет собой произведение многочлена на трансцендентную функцию (т.е. тригонометрическую, показательную, обратную тригонометрическую или логарифмическую), при этом:
· обратные тригонометрические и логарифмические функции принимают за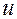 
;
· тригонометрические и показательные функции совместно с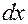 
за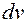 
.
Пример. Найти интеграл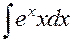 
, применив формулу интегрирования по частям.