Решение

 

Для этого два раза применим интегрирование по частям и получим в правой части равенства снова тот же интеграл I. Полученное равенство будем рассматривать как уравнение для нахождения I; решив его, получим ответ.

Итак,

 

 

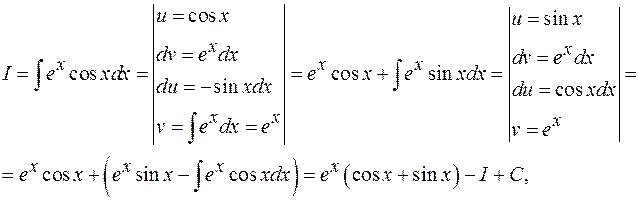
откуда, решая уравнение 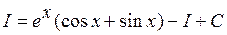относительно I, получаем: .

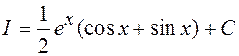Ответ: .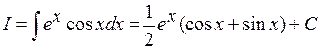

Интегрирование основных классов функций при помощи элементарных преобразований:

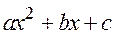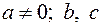а) Интегралы, содержащие квадратный трёхчлен , где - некоторые постоянные, вида:

 

 

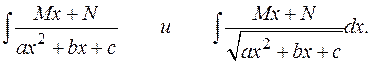
(Заметим, что в числителе дроби должно стоять линейное выражение 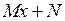, где М и N - постоянные; при этом какой-либо из постоянных величин не запрещается быть равной 0.)

 

 

Такие интегралы приводятся к табличным интегралам путём выделения из квадратного трёхчлена выражения, равного полному квадрату:

 

 

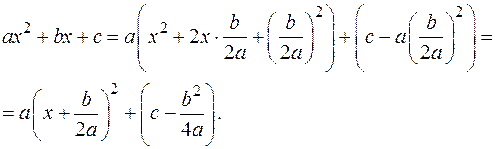
Затем выполняется замена 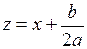, в результате которой получают интеграл одного из видов:

 

 

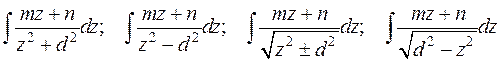
при некоторых постоянных 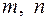и d. Далее разбиваем интеграл на два слагаемых и в первом, в числителе подынтегральной функции, содержащем mz, делаем замену 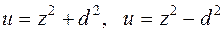или 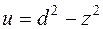, согласно тому, что стоит в знаменателе. После этого первое слагаемое приводится к табличному интегралу, второе слагаемое, c n в числителе подынтегральной функции, тоже даёт табличный интеграл.

Пример. Вычислить интеграл 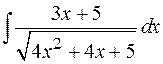.